2020年秋人教版九年级数学上册随堂练——23.3课题学习图案设计提升练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练——23.3课题学习图案设计提升练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览

文档简介
23.3课题学习图案设计提升练习
一、选择题
1.下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A.
B.
C.
D.
2.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有(
)
A.1种
B.2种
C.3种
D.4种
3.如图所示,先将图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形是( )
A.?
B.?
C.?
D.?
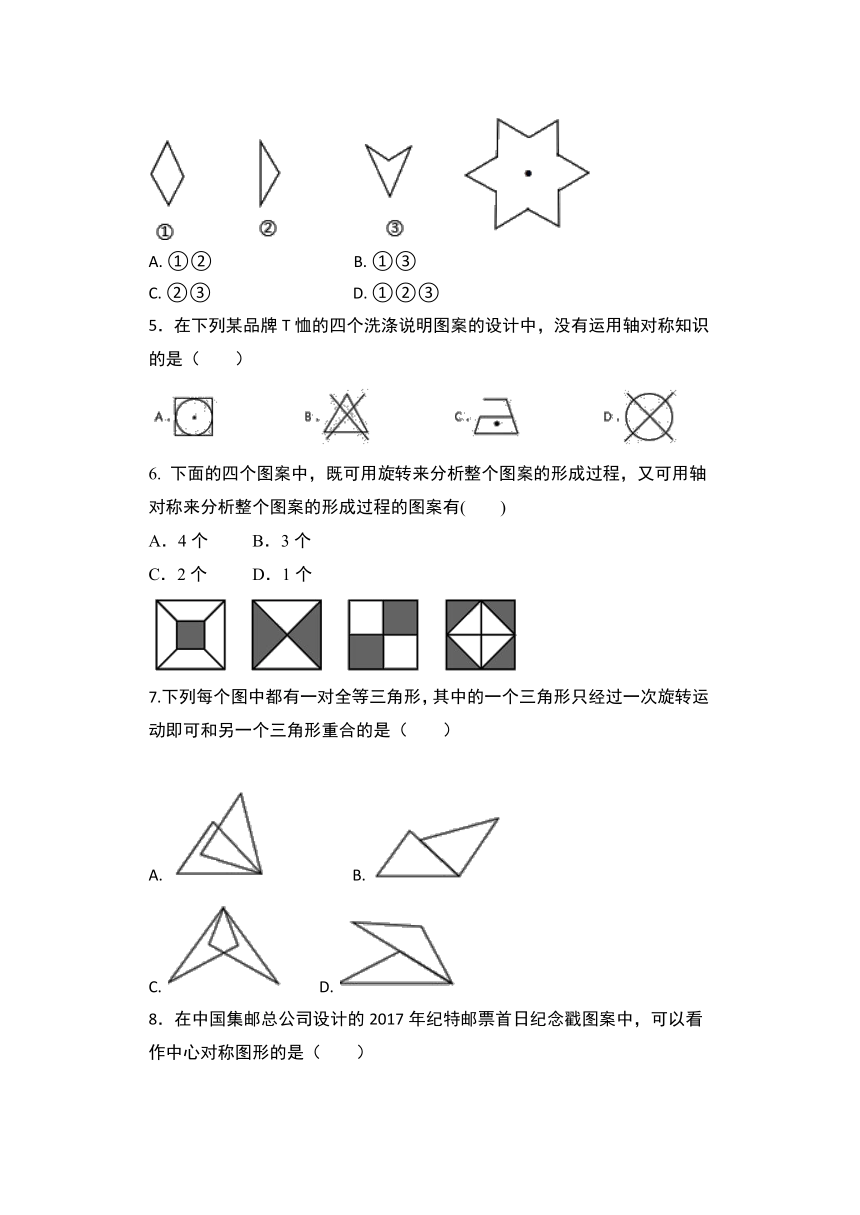
4.下列3个图形中,能通过旋转得到右侧图形的有(?
)
A.?①②????????????????????????????????????B.?①③????????????????????????????????????
C.?②③????????????????????????????????????D.?①②③
5.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用轴对称知识的是( )
6.
下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有(
)
A.4个
B.3个
C.2个
D.1个
7.下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是( )
A.?
B.?
C.?
D.?
8.在中国集邮总公司设计的2017年纪特邮票首日纪念戳图案中,可以看作中心对称图形的是( )
A.
B.
C.
D.
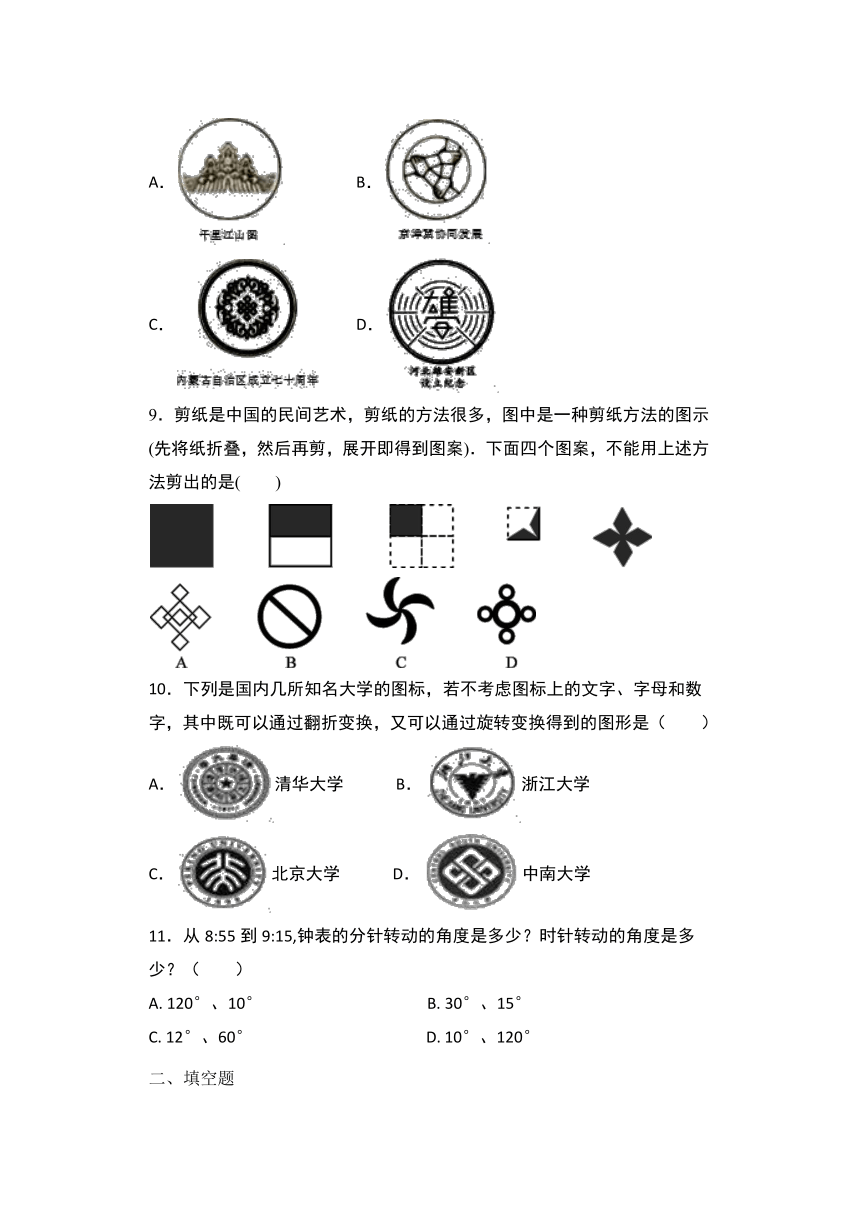
9.剪纸是中国的民间艺术,剪纸的方法很多,图中是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案).下面四个图案,不能用上述方法剪出的是(
)
10.下列是国内几所知名大学的图标,若不考虑图标上的文字、字母和数字,其中既可以通过翻折变换,又可以通过旋转变换得到的图形是( )
A.清华大学
B.浙江大学
C.北京大学
D.中南大学
11.从8:55到9:15,钟表的分针转动的角度是多少?时针转动的角度是多少?( )
A.
120°、10°?
B.
30°、15°?
C.
12°、60°?
D.
10°、120°
二、填空题
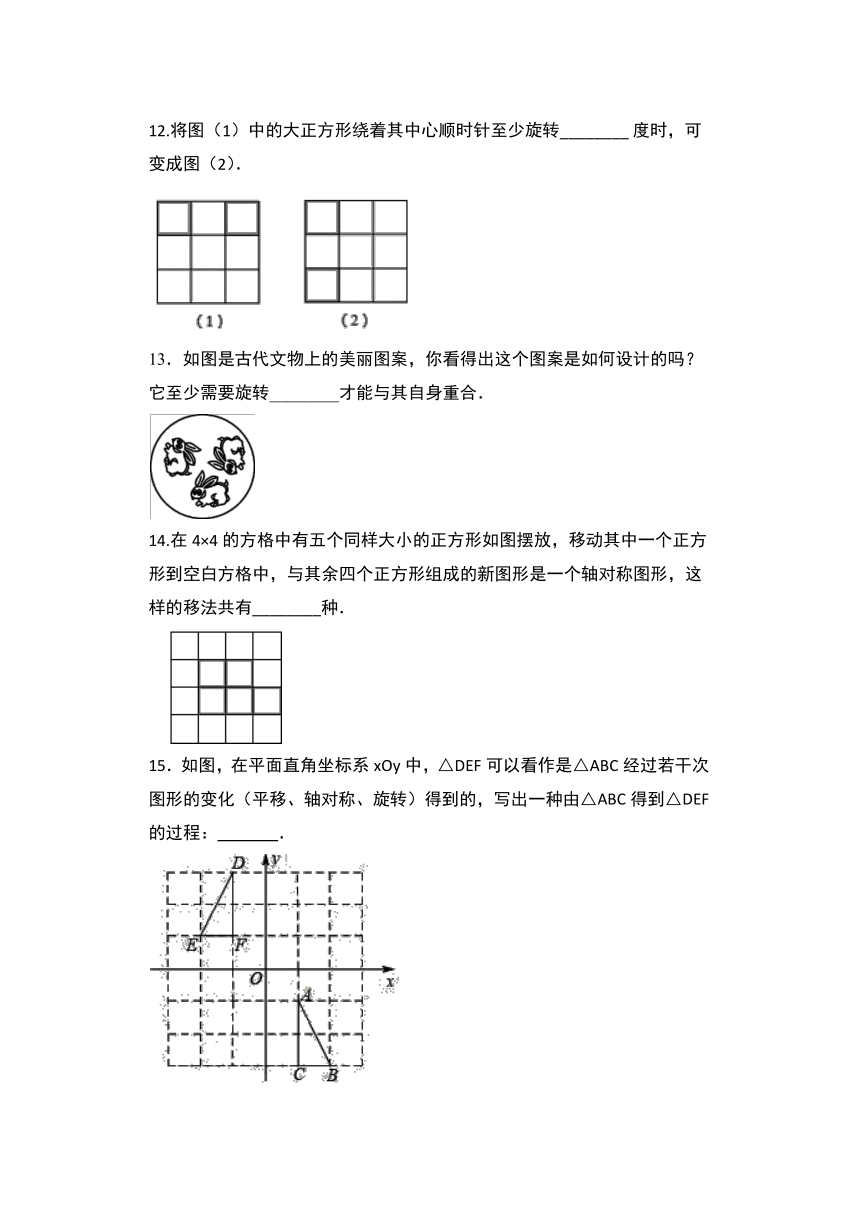
12.将图(1)中的大正方形绕着其中心顺时针至少旋转________?度时,可变成图(2).
13.如图是古代文物上的美丽图案,你看得出这个图案是如何设计的吗?它至少需要旋转________才能与其自身重合.
14.在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有________种.
15.如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:
.
16.
已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为SA、SB(网格中最小的正方形面积为一个平方单位),则SA∶SB的值是_________;
17.如图,将其补全,使其成为中心对称图形.
18.在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有
种.
19.
下列3个图形中,能通过旋转得到右侧图形的有____________.(填序号)
三、解答题
20.如图
,它是由哪个基本图形经过怎样的变化得到的?
21.图
所示的4个图案有什么共同特征?
22.
已知,点P是正方形ABCD内的一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图
①).
①设AB的长为a,PB的长为b(b②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图
②,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
?
23.如图,阴影部分是由5个小正方形组成的一个直角图形,请用三种不同方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.答案涂在答卷相应的位置.
24.
现有如图23-3-4①所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼成的图案是轴对称图形或中心对称图形(如示例图②).
(要求:分别在图③、图④中设计一种与示例图不同的拼法,这两种拼法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
25.
为创建绿色校园,学校决定在一块正方形的空地上种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案是轴对称图形.种植花草部分用阴影表示.请你在图③,图④,图⑤中画出三种不同的设计图案.提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①,图②只能算一种.
答案
1.
C
2.
C
3.
A
4.
B
5.
C
6.
A
7.
D
8.
C
9.
C
10.
A
11.
A
12.
270.
13.
120°
14.
13
15.
平移,轴对称.
16.
9∶11
17.
如图所示:就是中心对称图形.
18.
4.
19.
①②③
20.
是由基本图形向右平移,再向下平移,再向左平移,然后再由基本图形?
向右平移,再向下平移,再向左平移得到的.
21.
共同点:都是由一个基本图形经过平移(或旋转)得到的.
22.
解:(1)①S阴影=πa2-πb2=
(a2-b2).?
②连接PP′,由旋转可得:△PBP′为等腰直角三角形,∠APB=∠CP′B=135°.所以∠PP′C=90°.由勾股定理,可得PC=.?
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,连接PP′,由勾股定理,可得PB2+P′B2=P′P2,即2PB2=P′P2.又因为PA2+PC2=2PB2,所以PA2+PC2=P′P2.由勾股逆定理,得∠P′CP=90°后,再证∠BPC+∠APB=180°,即点P在对角线AC上.?
23.
如图所示:
24.
解:答案不唯一,如图所示.
25.
解:答案不唯一,如图
一、选择题
1.下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A.
B.
C.
D.
2.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有(
)
A.1种
B.2种
C.3种
D.4种
3.如图所示,先将图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形是( )
A.?
B.?
C.?
D.?
4.下列3个图形中,能通过旋转得到右侧图形的有(?
)
A.?①②????????????????????????????????????B.?①③????????????????????????????????????
C.?②③????????????????????????????????????D.?①②③
5.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用轴对称知识的是( )
6.
下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有(
)
A.4个
B.3个
C.2个
D.1个
7.下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是( )
A.?
B.?
C.?
D.?
8.在中国集邮总公司设计的2017年纪特邮票首日纪念戳图案中,可以看作中心对称图形的是( )
A.
B.
C.
D.
9.剪纸是中国的民间艺术,剪纸的方法很多,图中是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案).下面四个图案,不能用上述方法剪出的是(
)
10.下列是国内几所知名大学的图标,若不考虑图标上的文字、字母和数字,其中既可以通过翻折变换,又可以通过旋转变换得到的图形是( )
A.清华大学
B.浙江大学
C.北京大学
D.中南大学
11.从8:55到9:15,钟表的分针转动的角度是多少?时针转动的角度是多少?( )
A.
120°、10°?
B.
30°、15°?
C.
12°、60°?
D.
10°、120°
二、填空题
12.将图(1)中的大正方形绕着其中心顺时针至少旋转________?度时,可变成图(2).
13.如图是古代文物上的美丽图案,你看得出这个图案是如何设计的吗?它至少需要旋转________才能与其自身重合.
14.在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有________种.
15.如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:
.
16.
已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为SA、SB(网格中最小的正方形面积为一个平方单位),则SA∶SB的值是_________;
17.如图,将其补全,使其成为中心对称图形.
18.在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有
种.
19.
下列3个图形中,能通过旋转得到右侧图形的有____________.(填序号)
三、解答题
20.如图
,它是由哪个基本图形经过怎样的变化得到的?
21.图
所示的4个图案有什么共同特征?
22.
已知,点P是正方形ABCD内的一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图
①).
①设AB的长为a,PB的长为b(b
(2)如图
②,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
?
23.如图,阴影部分是由5个小正方形组成的一个直角图形,请用三种不同方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.答案涂在答卷相应的位置.
24.
现有如图23-3-4①所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼成的图案是轴对称图形或中心对称图形(如示例图②).
(要求:分别在图③、图④中设计一种与示例图不同的拼法,这两种拼法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
25.
为创建绿色校园,学校决定在一块正方形的空地上种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案是轴对称图形.种植花草部分用阴影表示.请你在图③,图④,图⑤中画出三种不同的设计图案.提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①,图②只能算一种.
答案
1.
C
2.
C
3.
A
4.
B
5.
C
6.
A
7.
D
8.
C
9.
C
10.
A
11.
A
12.
270.
13.
120°
14.
13
15.
平移,轴对称.
16.
9∶11
17.
如图所示:就是中心对称图形.
18.
4.
19.
①②③
20.
是由基本图形向右平移,再向下平移,再向左平移,然后再由基本图形?
向右平移,再向下平移,再向左平移得到的.
21.
共同点:都是由一个基本图形经过平移(或旋转)得到的.
22.
解:(1)①S阴影=πa2-πb2=
(a2-b2).?
②连接PP′,由旋转可得:△PBP′为等腰直角三角形,∠APB=∠CP′B=135°.所以∠PP′C=90°.由勾股定理,可得PC=.?
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,连接PP′,由勾股定理,可得PB2+P′B2=P′P2,即2PB2=P′P2.又因为PA2+PC2=2PB2,所以PA2+PC2=P′P2.由勾股逆定理,得∠P′CP=90°后,再证∠BPC+∠APB=180°,即点P在对角线AC上.?
23.
如图所示:
24.
解:答案不唯一,如图所示.
25.
解:答案不唯一,如图
同课章节目录
