2020年秋人教版九年级数学上册随堂练——23.3课题学习图案设计学情练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练——23.3课题学习图案设计学情练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览

文档简介
23.3课题学习图案设计学情练习
一、选择题
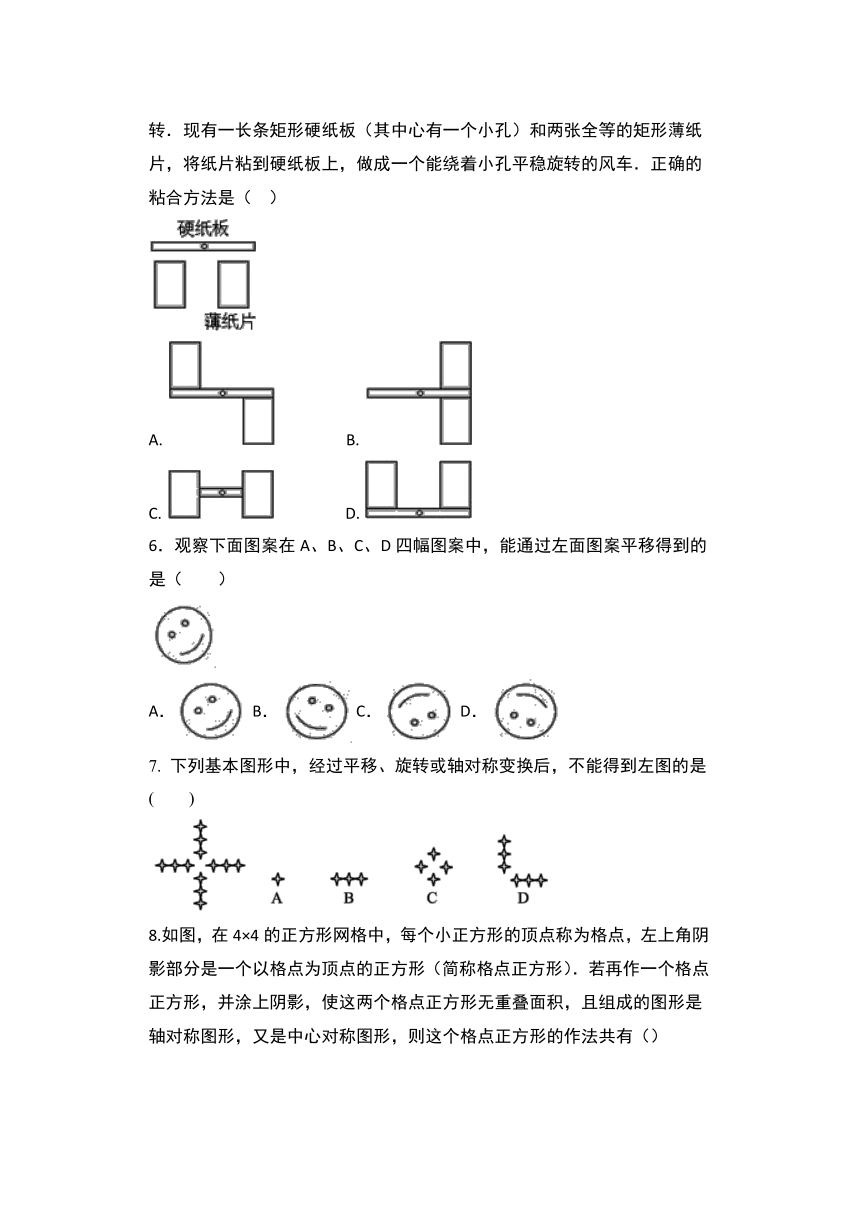
1.如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
A.?平移一次形成的
B.?平移两次形成的
C.?以轴心为旋转中心,旋转120°后形成的
D.?以轴心为旋转中心,旋转120°、240°后形成的
2.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
3.
下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(
)
4.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是(
)
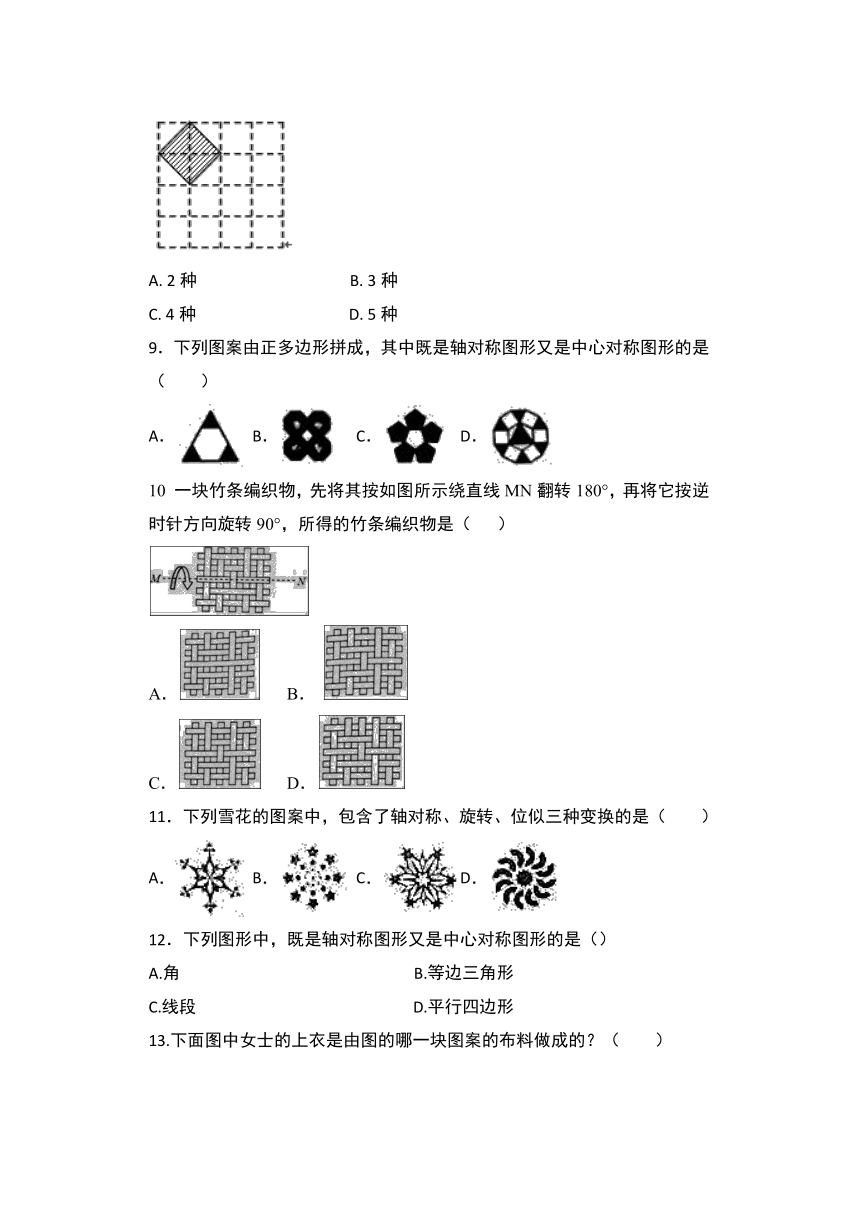
5.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的粘合方法是(??
)
A.???????????????????B.?????????????????
C.???????????????????D.?
6.观察下面图案在A、B、C、D四幅图案中,能通过左面图案平移得到的是( )
A.
B.
C.
D.
7.
下列基本图形中,经过平移、旋转或轴对称变换后,不能得到左图的是(
)
8.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有()
?
A.?2种???????????????????????????????????????B.?3种???????????????????????????????????????
C.?4种???????????????????????????????????????D.?5种
9.下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
10
一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是(
)
A.
B.
C.
D.
11.下列雪花的图案中,包含了轴对称、旋转、位似三种变换的是( )
A.
B.
C.
D.
12.下列图形中,既是轴对称图形又是中心对称图形的是()
A.角
?
B.等边三角形
C.线段?
D.平行四边形
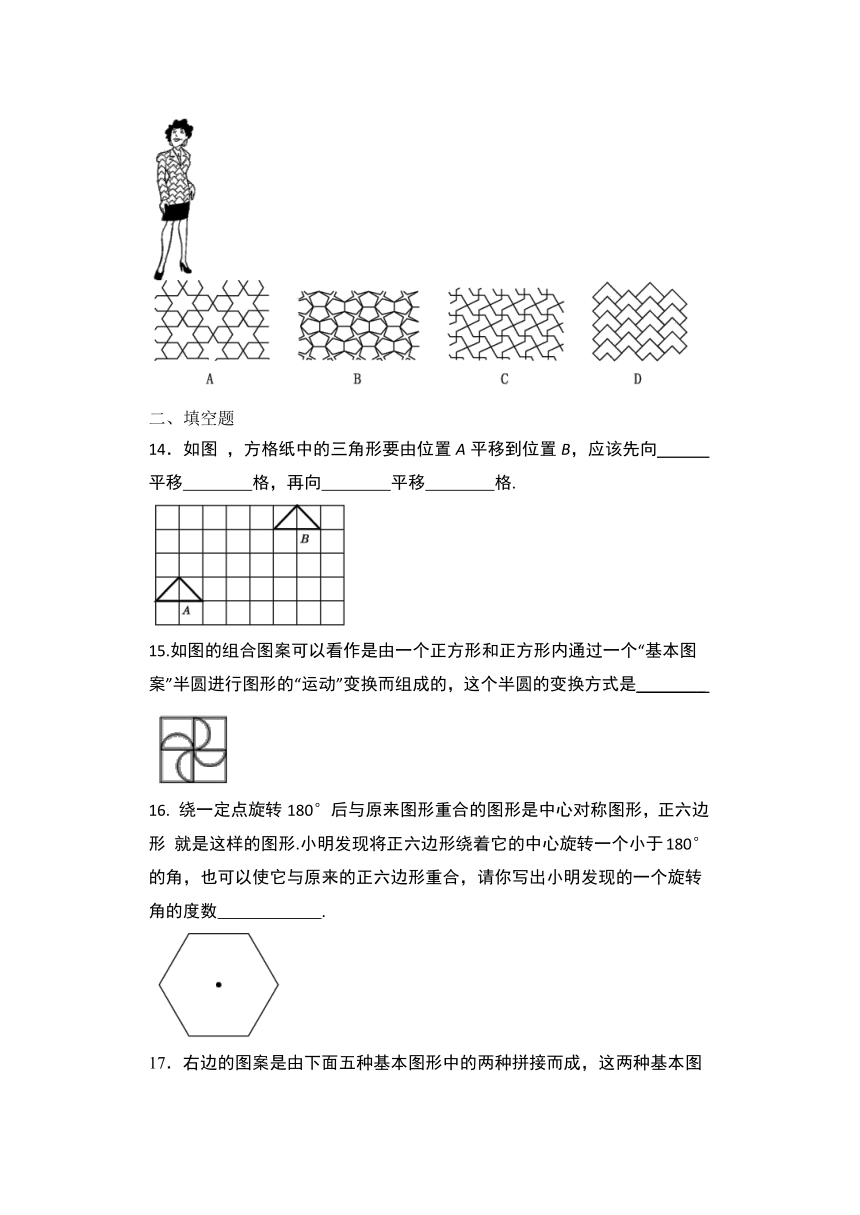
13.下面图中女士的上衣是由图的哪一块图案的布料做成的?( )
二、填空题
14.如图
,方格纸中的三角形要由位置A平移到位置B,应该先向
平移 格,再向 平移 格.
15.如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是________?
16.
绕一定点旋转180°后与原来图形重合的图形是中心对称图形,正六边形
就是这样的图形.小明发现将正六边形绕着它的中心旋转一个小于180°的角,也可以使它与原来的正六边形重合,请你写出小明发现的一个旋转角的度数 .
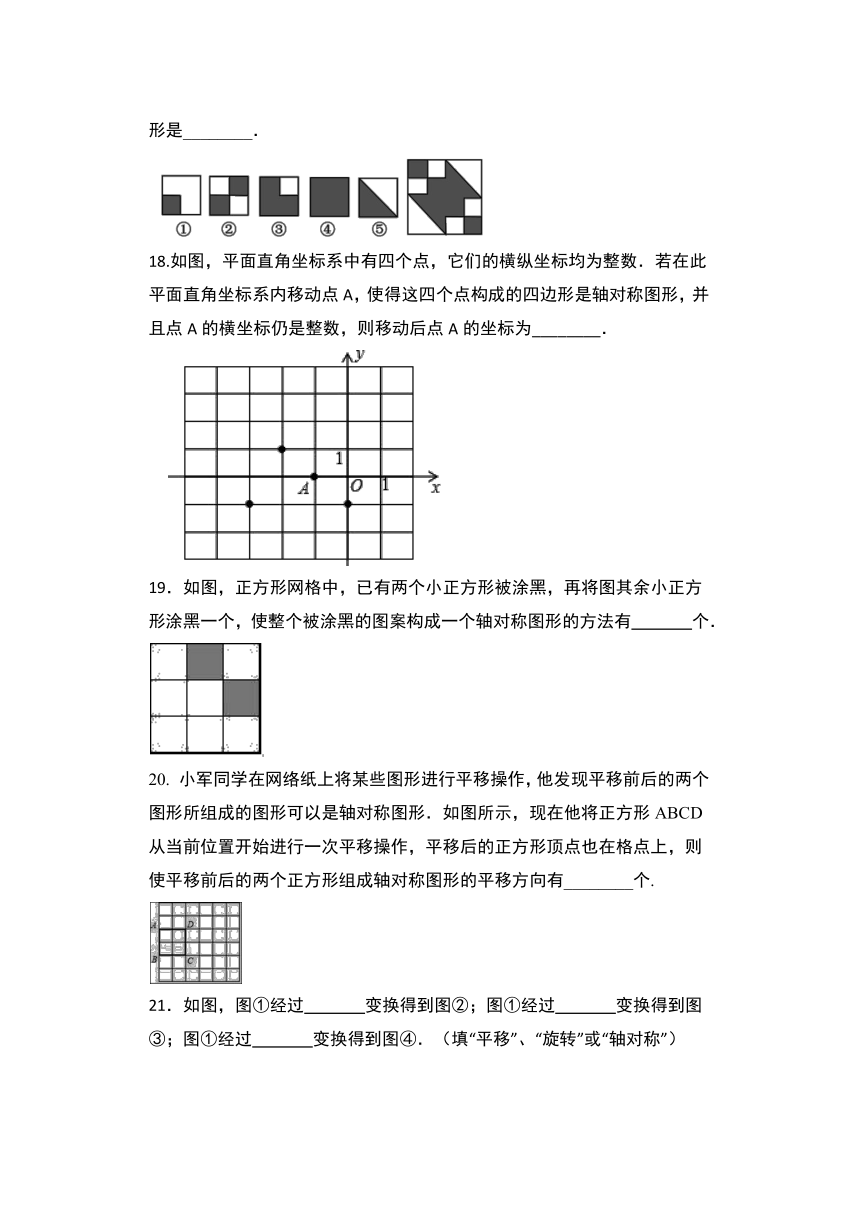
17.右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是________.
18.如图,平面直角坐标系中有四个点,它们的横纵坐标均为整数.若在此平面直角坐标系内移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横坐标仍是整数,则移动后点A的坐标为________.
19.如图,正方形网格中,已有两个小正方形被涂黑,再将图其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有
个.
20.
小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有________个.
21.如图,图①经过
变换得到图②;图①经过
变换得到图③;图①经过
变换得到图④.(填“平移”、“旋转”或“轴对称”)
三、解答题
22.在一个3m×4m的矩形地块上,欲开辟出一部分作花坛,要使花坛的面积为矩形面积的一半,且使整个图案绕它的中心旋转180°后能与自身重合,请给出你的设计方案.
23.
如图,网格中每个小正方形的边长为1,请你认真观察图①中的三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有以下共同特征:都是_______对称图形,都不是___对称图形;
(2)请在图②中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图1中给出的图案相同.
24.如图,在10×10正方形网格中,每个小正方形的边长均为1个长度单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请你画出△A′B′C′和△A″B″C′(不要求写画法).
25.
在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)
要求:
(1)5个小正方形必须相连(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
26.
观察设计.
(1)观察如图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;
(2)借助如图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图①~④的图案不能相同)
答案
1.
D
2.
C
3.
A
4.
C
5.
A
6.
A
7.
C
8.
C
9.
B
10
B
11.
B
12.
C??
13.
D
14.
上(或右) 3(或5) 右(或上) 5(或3)
15.
旋转
16.
60°
17.
②⑤
18.
(﹣1,1),(﹣2,﹣2),(0,2),(﹣2,﹣3)
19.
5
20.
5
21.
轴对称;旋转;平移.
22.
如图所示:答案不唯一.
23.
解:(1)中心,轴
(2)答案不唯一,只要符合条件即可,如图
24.
如图所示,△A′B′C′和△A″B″C′即为所求:
25.
解:如图.
26.
解:(1)答案不唯一,例如,所给的四个图案具有的共同特征可以是:
①是轴对称图形;
②面积都等于四个小正方形的面积之和;
③都是直线形图案;
④图案中不含钝角等.只要写出两个即可
(2)答案不唯一,只要设计的图案同时具有所给出的两个共同特征,均正确,例如,同时具备特征①,②的部分图案如图:
一、选择题
1.如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
A.?平移一次形成的
B.?平移两次形成的
C.?以轴心为旋转中心,旋转120°后形成的
D.?以轴心为旋转中心,旋转120°、240°后形成的
2.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
3.
下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(
)
4.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是(
)
5.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的粘合方法是(??
)
A.???????????????????B.?????????????????
C.???????????????????D.?
6.观察下面图案在A、B、C、D四幅图案中,能通过左面图案平移得到的是( )
A.
B.
C.
D.
7.
下列基本图形中,经过平移、旋转或轴对称变换后,不能得到左图的是(
)
8.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有()
?
A.?2种???????????????????????????????????????B.?3种???????????????????????????????????????
C.?4种???????????????????????????????????????D.?5种
9.下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
10
一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是(
)
A.
B.
C.
D.
11.下列雪花的图案中,包含了轴对称、旋转、位似三种变换的是( )
A.
B.
C.
D.
12.下列图形中,既是轴对称图形又是中心对称图形的是()
A.角
?
B.等边三角形
C.线段?
D.平行四边形
13.下面图中女士的上衣是由图的哪一块图案的布料做成的?( )
二、填空题
14.如图
,方格纸中的三角形要由位置A平移到位置B,应该先向
平移 格,再向 平移 格.
15.如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是________?
16.
绕一定点旋转180°后与原来图形重合的图形是中心对称图形,正六边形
就是这样的图形.小明发现将正六边形绕着它的中心旋转一个小于180°的角,也可以使它与原来的正六边形重合,请你写出小明发现的一个旋转角的度数 .
17.右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是________.
18.如图,平面直角坐标系中有四个点,它们的横纵坐标均为整数.若在此平面直角坐标系内移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横坐标仍是整数,则移动后点A的坐标为________.
19.如图,正方形网格中,已有两个小正方形被涂黑,再将图其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有
个.
20.
小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有________个.
21.如图,图①经过
变换得到图②;图①经过
变换得到图③;图①经过
变换得到图④.(填“平移”、“旋转”或“轴对称”)
三、解答题
22.在一个3m×4m的矩形地块上,欲开辟出一部分作花坛,要使花坛的面积为矩形面积的一半,且使整个图案绕它的中心旋转180°后能与自身重合,请给出你的设计方案.
23.
如图,网格中每个小正方形的边长为1,请你认真观察图①中的三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有以下共同特征:都是_______对称图形,都不是___对称图形;
(2)请在图②中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图1中给出的图案相同.
24.如图,在10×10正方形网格中,每个小正方形的边长均为1个长度单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请你画出△A′B′C′和△A″B″C′(不要求写画法).
25.
在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)
要求:
(1)5个小正方形必须相连(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
26.
观察设计.
(1)观察如图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;
(2)借助如图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图①~④的图案不能相同)
答案
1.
D
2.
C
3.
A
4.
C
5.
A
6.
A
7.
C
8.
C
9.
B
10
B
11.
B
12.
C??
13.
D
14.
上(或右) 3(或5) 右(或上) 5(或3)
15.
旋转
16.
60°
17.
②⑤
18.
(﹣1,1),(﹣2,﹣2),(0,2),(﹣2,﹣3)
19.
5
20.
5
21.
轴对称;旋转;平移.
22.
如图所示:答案不唯一.
23.
解:(1)中心,轴
(2)答案不唯一,只要符合条件即可,如图
24.
如图所示,△A′B′C′和△A″B″C′即为所求:
25.
解:如图.
26.
解:(1)答案不唯一,例如,所给的四个图案具有的共同特征可以是:
①是轴对称图形;
②面积都等于四个小正方形的面积之和;
③都是直线形图案;
④图案中不含钝角等.只要写出两个即可
(2)答案不唯一,只要设计的图案同时具有所给出的两个共同特征,均正确,例如,同时具备特征①,②的部分图案如图:
同课章节目录
