11.2三角形全等的判定(SAS)
文档属性
| 名称 | 11.2三角形全等的判定(SAS) |  | |
| 格式 | rar | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-22 21:13:10 | ||
图片预览


文档简介
(共13张PPT)
11.2三角形全等的判定
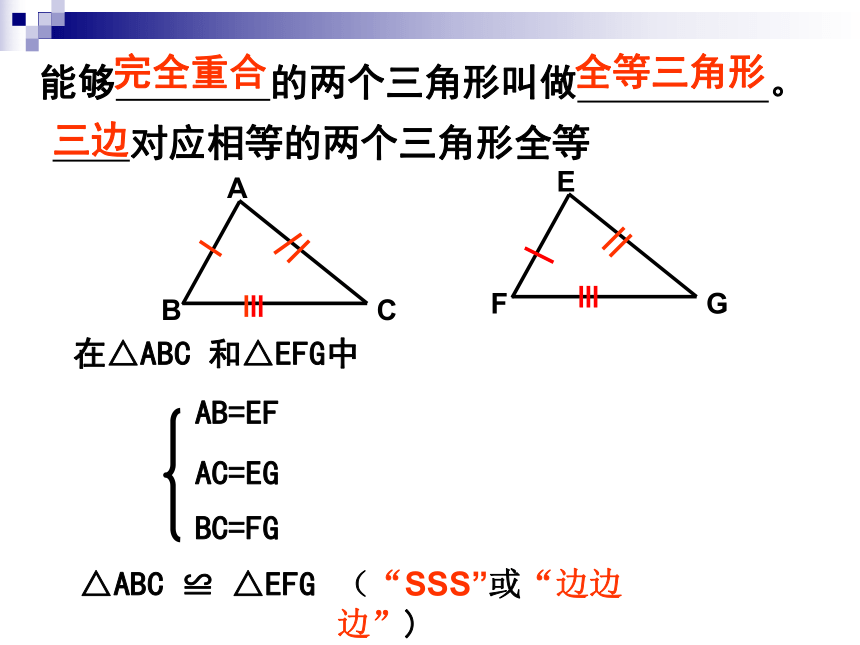
对应相等的两个三角形全等
三边
A
B
C
E
F
G
在△ABC 和△EFG中
△ABC ≌ △EFG
(“SSS”或“边边边”)
AB=EF
AC=EG
BC=FG
能够 的两个三角形叫做 。
完全重合
全等三角形
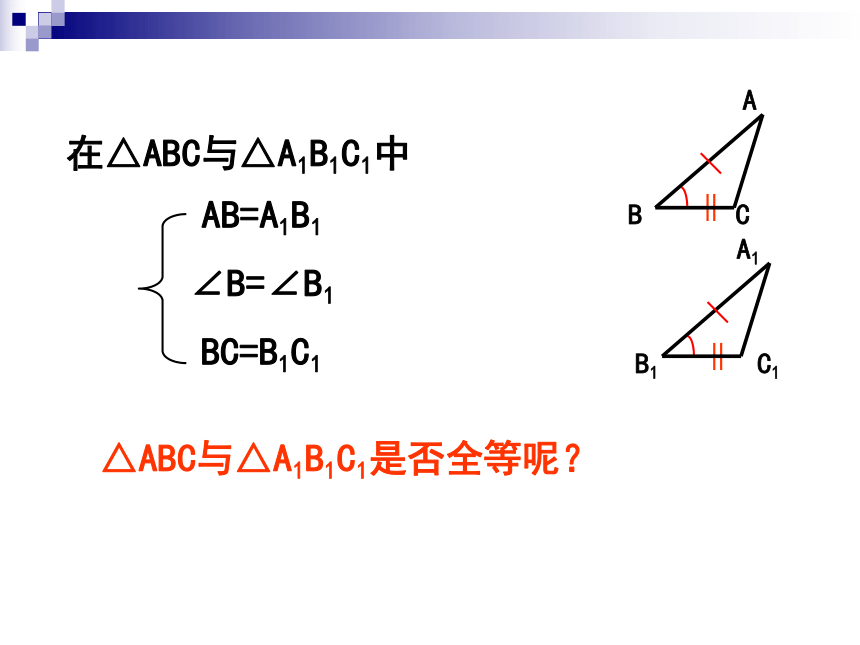
∠B=∠B1
BC=B1C1
△ABC与△A1B1C1是否全等呢?
在△ABC与△A1B1C1中
A
B
C
A1
B1
C1
AB=A1B1
做一做: 先任意画出一个△ABC,再画出一个△A1B1C1,,使A1B1=AB,A1C1=AC,∠A1=∠A(即使两边和他们的夹角对应相等)。把画好的三角形剪下来,放到△ABC上,他们全等么?
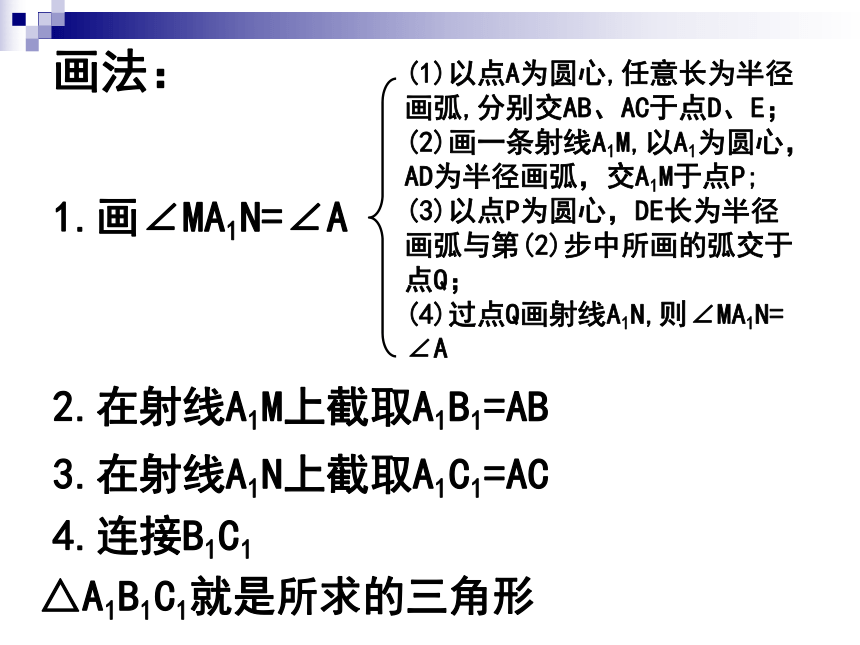
画法:
2.在射线A1M上截取A1B1=AB
3.在射线A1N上截取A1C1=AC
1.画∠MA1N=∠A
4.连接B1C1
△A1B1C1就是所求的三角形
(1)以点A为圆心,任意长为半径画弧,分别交AB、AC于点D、E;
(2)画一条射线A1M,以A1为圆心,AD为半径画弧,交A1M于点P;
(3)以点P为圆心,DE长为半径画弧与第(2)步中所画的弧交于点Q;
(4)过点Q画射线A1N,则∠MA1N= ∠A
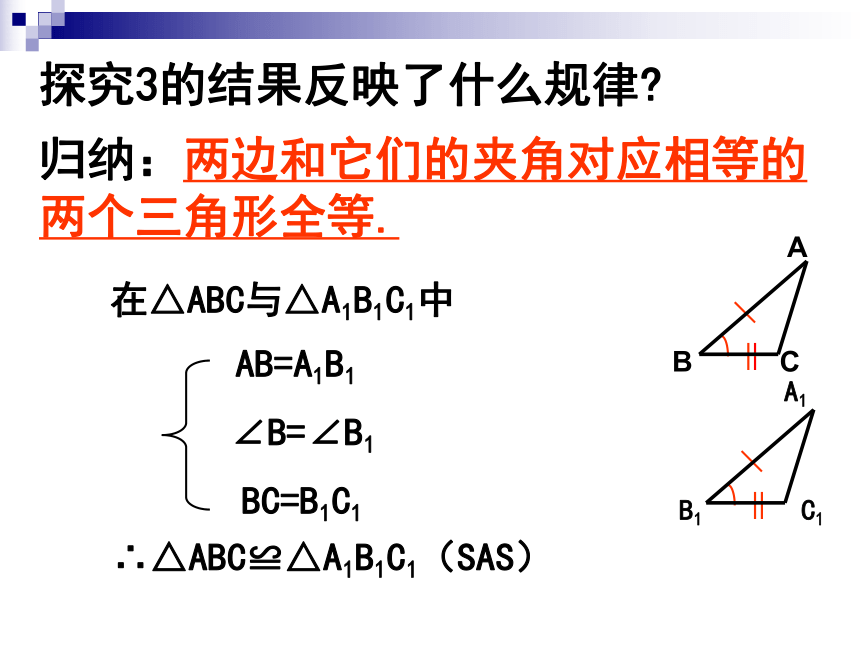
探究3的结果反映了什么规律
归纳:两边和它们的夹角对应相等的两个三角形全等.
∴△ABC≌△A1B1C1(SAS)
AB=A1B1
∠B=∠B1
BC=B1C1
C1
在△ABC与△A1B1C1中
A
B
C
A1
B1
典例解析
例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?
分析:如果能证明△ABC ≌△DEC,
就可以得出AB=DE
在△ABC 和△DEC中,CA=CD,CB=CE.
如果能得出∠1=∠2,
△ABC 和△DEC就全等了.
典例解析
例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?
证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴AB=DE(全等三角形的对应边相等)
CA=CD(已知)
∠1=∠2(对顶角)
CB=CE(已知)
当堂达标:
1、如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C、D两地,此时C,D到B的距离相等吗?为什么?
D
C
A
B
在△ABC和△ABD中AB=AB(公共边)∠BAC=∠BAD(垂直)AC=AD(已知)
证明:
∴ △ABC≌△ABD(SAS)
∴BC=BD(全等三角形的对应边相等)
2、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C。求证∠A=∠D
B
E
F
C
A
D
证明:
在△ABF和△DCE中
∵BE=CF∴BE+EF=CF+EF即BF=CE
AB=DC(已知)
∠B=∠C(已知)
BF=CE(已证)
∴ △ABF≌△DCE(SAS)
∴ ∠A=∠D(全等三角形的对应角相等)
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
探究4
如图△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠B
B
A
C
D
他们全等吗?
结论:两边及其一边所对的角相等,两个三角形不一定全等
布置作业:
必做题:课本习题11.2第3题、第4题
选做题:1、课本习题11.2第10题
2、交流探究 (1)、你是否能找到两边及其夹角对应相等而不全等的两个三角形?
(2)、你是否还能找到其它方法来判定两个三角形全等?
再见
11.2三角形全等的判定
对应相等的两个三角形全等
三边
A
B
C
E
F
G
在△ABC 和△EFG中
△ABC ≌ △EFG
(“SSS”或“边边边”)
AB=EF
AC=EG
BC=FG
能够 的两个三角形叫做 。
完全重合
全等三角形
∠B=∠B1
BC=B1C1
△ABC与△A1B1C1是否全等呢?
在△ABC与△A1B1C1中
A
B
C
A1
B1
C1
AB=A1B1
做一做: 先任意画出一个△ABC,再画出一个△A1B1C1,,使A1B1=AB,A1C1=AC,∠A1=∠A(即使两边和他们的夹角对应相等)。把画好的三角形剪下来,放到△ABC上,他们全等么?
画法:
2.在射线A1M上截取A1B1=AB
3.在射线A1N上截取A1C1=AC
1.画∠MA1N=∠A
4.连接B1C1
△A1B1C1就是所求的三角形
(1)以点A为圆心,任意长为半径画弧,分别交AB、AC于点D、E;
(2)画一条射线A1M,以A1为圆心,AD为半径画弧,交A1M于点P;
(3)以点P为圆心,DE长为半径画弧与第(2)步中所画的弧交于点Q;
(4)过点Q画射线A1N,则∠MA1N= ∠A
探究3的结果反映了什么规律
归纳:两边和它们的夹角对应相等的两个三角形全等.
∴△ABC≌△A1B1C1(SAS)
AB=A1B1
∠B=∠B1
BC=B1C1
C1
在△ABC与△A1B1C1中
A
B
C
A1
B1
典例解析
例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?
分析:如果能证明△ABC ≌△DEC,
就可以得出AB=DE
在△ABC 和△DEC中,CA=CD,CB=CE.
如果能得出∠1=∠2,
△ABC 和△DEC就全等了.
典例解析
例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?
证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴AB=DE(全等三角形的对应边相等)
CA=CD(已知)
∠1=∠2(对顶角)
CB=CE(已知)
当堂达标:
1、如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C、D两地,此时C,D到B的距离相等吗?为什么?
D
C
A
B
在△ABC和△ABD中AB=AB(公共边)∠BAC=∠BAD(垂直)AC=AD(已知)
证明:
∴ △ABC≌△ABD(SAS)
∴BC=BD(全等三角形的对应边相等)
2、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C。求证∠A=∠D
B
E
F
C
A
D
证明:
在△ABF和△DCE中
∵BE=CF∴BE+EF=CF+EF即BF=CE
AB=DC(已知)
∠B=∠C(已知)
BF=CE(已证)
∴ △ABF≌△DCE(SAS)
∴ ∠A=∠D(全等三角形的对应角相等)
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
探究4
如图△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠B
B
A
C
D
他们全等吗?
结论:两边及其一边所对的角相等,两个三角形不一定全等
布置作业:
必做题:课本习题11.2第3题、第4题
选做题:1、课本习题11.2第10题
2、交流探究 (1)、你是否能找到两边及其夹角对应相等而不全等的两个三角形?
(2)、你是否还能找到其它方法来判定两个三角形全等?
再见
