三角形中位线 课件
图片预览





文档简介
(共21张PPT)
三角形中位线
教学重点
教学难点
三角形中位线定理及其应用
三角形中位线定理的证明及应用
知识目标
1.理解三角形中位线的概念
2.掌握三角形中位线的定理
3.初步学会用三角形中位线定理
解决一些实际问题
返回
能力目标
1.培养学生实验观察.分析探究.归纳总结.推理论证的能力
2.培养学生发散思维及创新学习能力
返回
情感目标
1.培养学生科学分析的态度和积极的探索精神。
2.向学生渗透运动变化及理论来与实践的辩证唯物主义世界观的思想。
3.激发学生学习的积极性,提高学生学习数学的兴趣。
返回
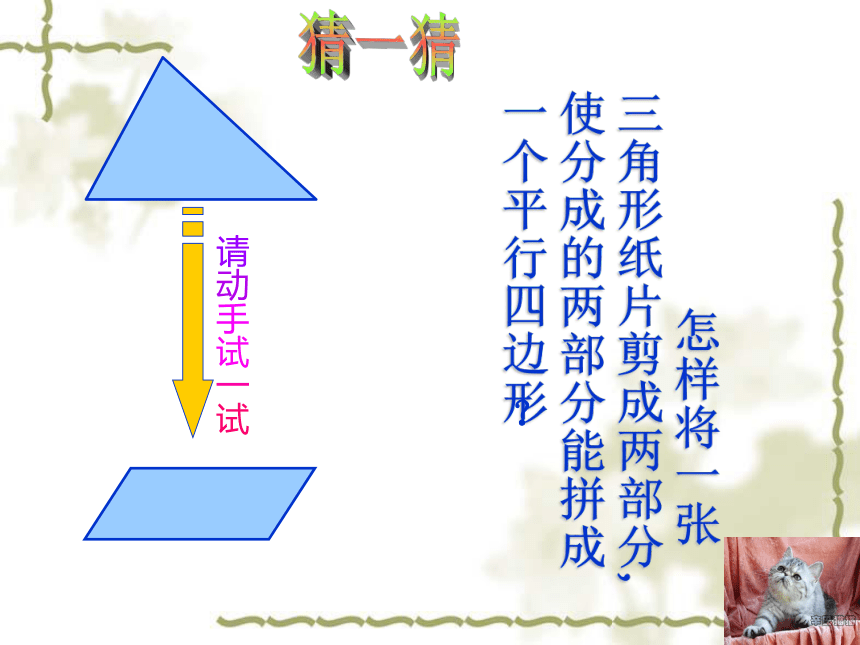
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形
请动手试一试
?
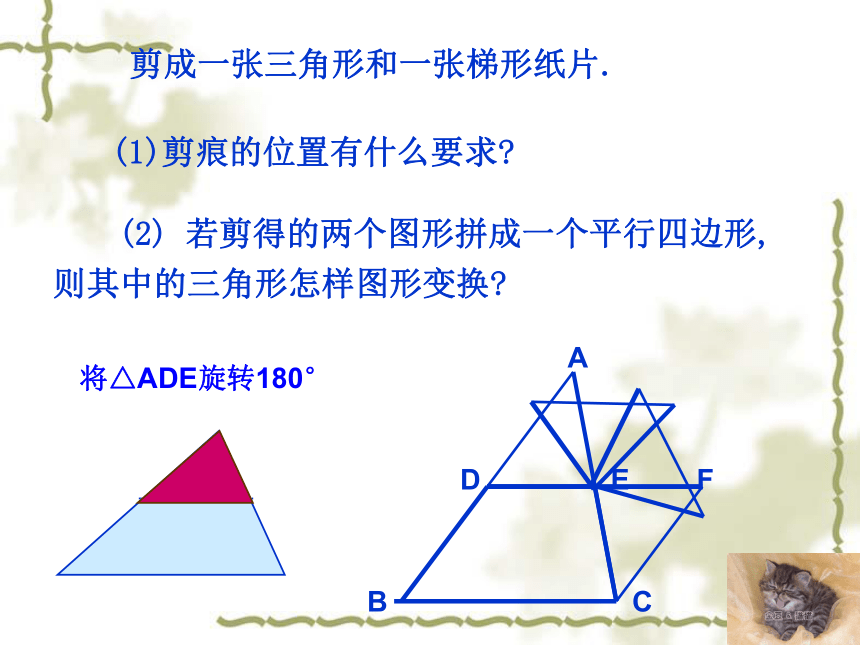
剪成一张三角形和一张梯形纸片.
(2) 若剪得的两个图形拼成一个平行四边形,则其中的三角形怎样图形变换
(1)剪痕的位置有什么要求
A
D
C
E
B
F
将△ADE旋转180°
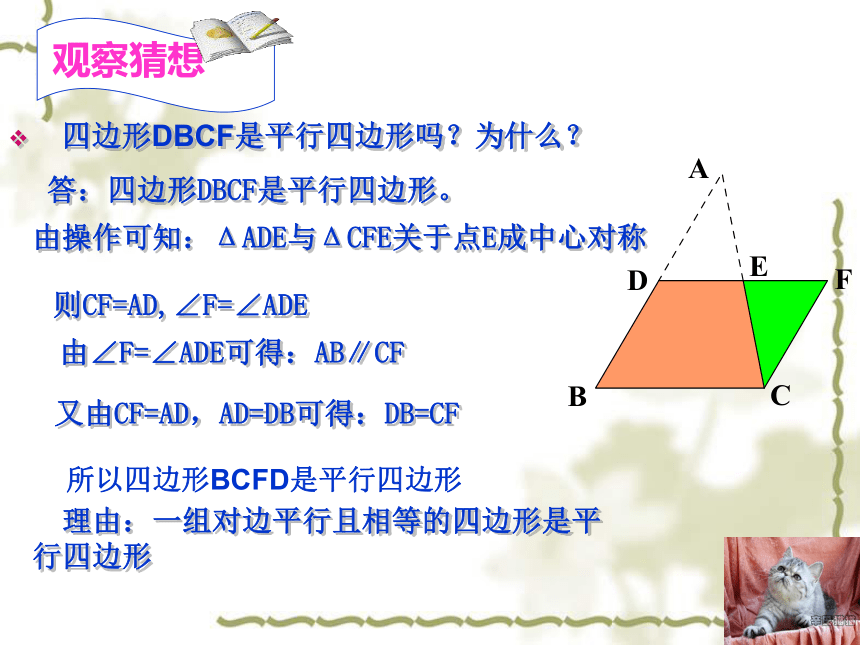
四边形DBCF是平行四边形吗?为什么?
答:四边形DBCF是平行四边形。
由操作可知:ΔADE与ΔCFE关于点E成中心对称
则CF=AD,∠F=∠ADE
由∠F=∠ADE可得:AB∥CF
又由CF=AD,AD=DB可得:DB=CF
理由:一组对边平行且相等的四边形是平行四边形
观察猜想
所以四边形BCFD是平行四边形
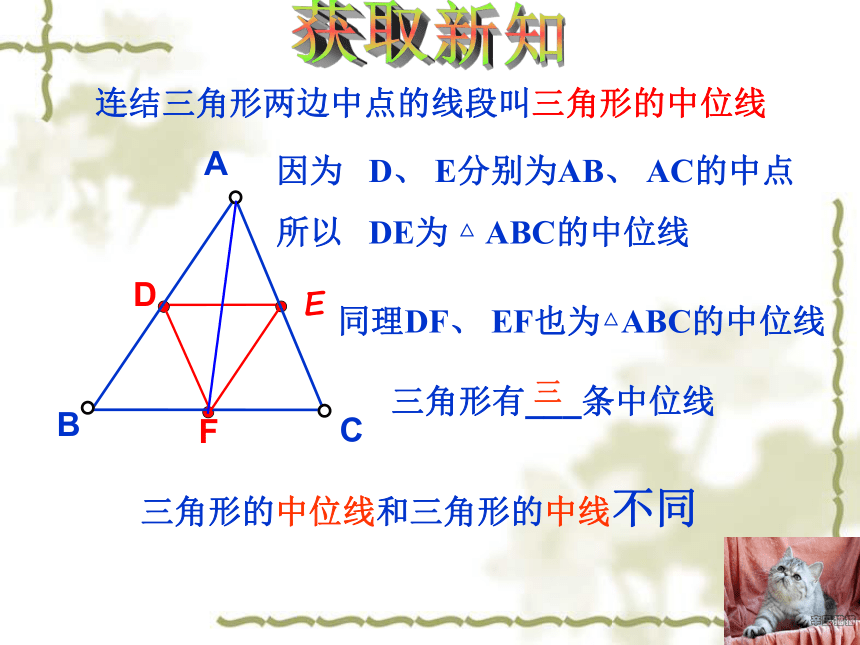
连结三角形两边中点的线段叫三角形的中位线
三角形有___条中位线
因为 D、 E分别为AB、 AC的中点
所以 DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同
同理DF、 EF也为△ABC的中位线
E
D
F
A
C
B
三
ΔABC的中位线DE与BC有怎样的位置和数量关系?
为什么?
答:DE∥BC,DE= BC
通过探索得知:四边形BCFD是平行四边形
则DF∥BC DF=BC
又由操作可知 ΔADE与ΔCFE关于点E成中心对称
∴DE=EF= DF ∴DE∥BC DE= BC
由此得出:三角形中位线的性质:
三角形的中位线平行于第三边,并且等于它的一半。
即 ①DE∥BC,②DE= BC
↓ ↓
位置关系 数量关系
1.已知:△ABC中,D.E.F分别是边AB.BC.AC的中点AB=12,BC=10,AC=8,
DE=( ),EF=( ) ,DF= ( ),
△DEF的周长为( )
2.已知: △ABC的周长为60cm,中位线DE=8cm,EF=12cm,则另一条中位线的长为( )
已知:如图,在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
分析,由E,F,G,H分别四边形
各边的中点,联想到应用三角形的
中位线定理来证明
顺次连接四边形各边中点的线段组成一个___________
平行四边形
2.如图所示,△ABC
中线BD、CE相交于O,F、G分别为OB、OC的中点。求证:四边形DEFG为平行四边形。
我来应战
●
●
A
E
C
B
F
测量两点之间不能到达的距离的方法:------中位线法
本课小结
1.理解三角形中位线的概念:连接三角形两边中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:三角形的中位线平行于第三边,并且等于它的一半。
3.能应用三角形中位线的性质解决有关计算或说理等问题。
回顾 思考
三角形中位线
教学重点
教学难点
三角形中位线定理及其应用
三角形中位线定理的证明及应用
知识目标
1.理解三角形中位线的概念
2.掌握三角形中位线的定理
3.初步学会用三角形中位线定理
解决一些实际问题
返回
能力目标
1.培养学生实验观察.分析探究.归纳总结.推理论证的能力
2.培养学生发散思维及创新学习能力
返回
情感目标
1.培养学生科学分析的态度和积极的探索精神。
2.向学生渗透运动变化及理论来与实践的辩证唯物主义世界观的思想。
3.激发学生学习的积极性,提高学生学习数学的兴趣。
返回
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形
请动手试一试
?
剪成一张三角形和一张梯形纸片.
(2) 若剪得的两个图形拼成一个平行四边形,则其中的三角形怎样图形变换
(1)剪痕的位置有什么要求
A
D
C
E
B
F
将△ADE旋转180°
四边形DBCF是平行四边形吗?为什么?
答:四边形DBCF是平行四边形。
由操作可知:ΔADE与ΔCFE关于点E成中心对称
则CF=AD,∠F=∠ADE
由∠F=∠ADE可得:AB∥CF
又由CF=AD,AD=DB可得:DB=CF
理由:一组对边平行且相等的四边形是平行四边形
观察猜想
所以四边形BCFD是平行四边形
连结三角形两边中点的线段叫三角形的中位线
三角形有___条中位线
因为 D、 E分别为AB、 AC的中点
所以 DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同
同理DF、 EF也为△ABC的中位线
E
D
F
A
C
B
三
ΔABC的中位线DE与BC有怎样的位置和数量关系?
为什么?
答:DE∥BC,DE= BC
通过探索得知:四边形BCFD是平行四边形
则DF∥BC DF=BC
又由操作可知 ΔADE与ΔCFE关于点E成中心对称
∴DE=EF= DF ∴DE∥BC DE= BC
由此得出:三角形中位线的性质:
三角形的中位线平行于第三边,并且等于它的一半。
即 ①DE∥BC,②DE= BC
↓ ↓
位置关系 数量关系
1.已知:△ABC中,D.E.F分别是边AB.BC.AC的中点AB=12,BC=10,AC=8,
DE=( ),EF=( ) ,DF= ( ),
△DEF的周长为( )
2.已知: △ABC的周长为60cm,中位线DE=8cm,EF=12cm,则另一条中位线的长为( )
已知:如图,在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
分析,由E,F,G,H分别四边形
各边的中点,联想到应用三角形的
中位线定理来证明
顺次连接四边形各边中点的线段组成一个___________
平行四边形
2.如图所示,△ABC
中线BD、CE相交于O,F、G分别为OB、OC的中点。求证:四边形DEFG为平行四边形。
我来应战
●
●
A
E
C
B
F
测量两点之间不能到达的距离的方法:------中位线法
本课小结
1.理解三角形中位线的概念:连接三角形两边中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:三角形的中位线平行于第三边,并且等于它的一半。
3.能应用三角形中位线的性质解决有关计算或说理等问题。
回顾 思考
