15.1同底数幂的乘法 课件
文档属性
| 名称 | 15.1同底数幂的乘法 课件 |  | |
| 格式 | rar | ||
| 文件大小 | 458.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-22 23:04:32 | ||
图片预览





文档简介
(共20张PPT)
15.1.1 同底数幂的乘法
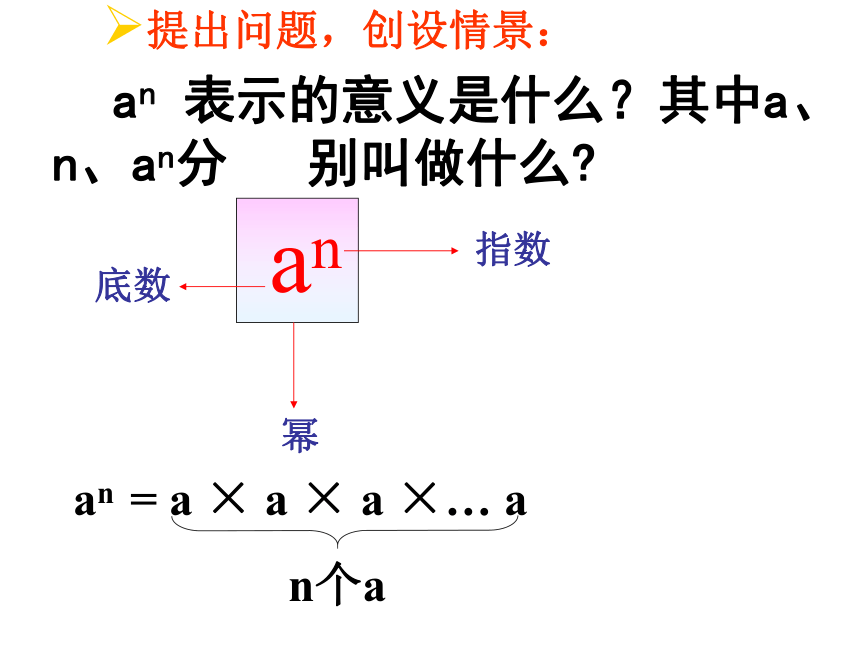
an 表示的意义是什么?其中a、n、an分 别叫做什么
an
底数
幂
指数
提出问题,创设情景:
an = a × a × a ×… a
n个a
25表示什么?
问题:
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
(乘方的意义)
(乘方的意义)
10×10×10×10×10 可以写成什么形式
式子103×102的意义是什么?
思考:
103与102 的积
底数相同
这个式子中的两个因式有何特点?
请同学们先根据自己的理解,解答下列各题.
103 ×102 =(10×10×10)×(10×10) = 10( )
23 ×22 = =2( )
5
(2×2×2)×(2×2)
5
a3×a2 = = a( ) .
5
(a a a)
(a a)
=2×2×2×2×2
= a a a a a
3个a
2个a
5个a
探究在线:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103 ×102 = 10( )
23 ×22 = 2( )
a3× a2 = a( )
5
5
5
猜想: am · an= (当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确.
3+2
3+2
3+2
= 10( );
= 2( );
= a( ) 。
猜想: am · an= am+n (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
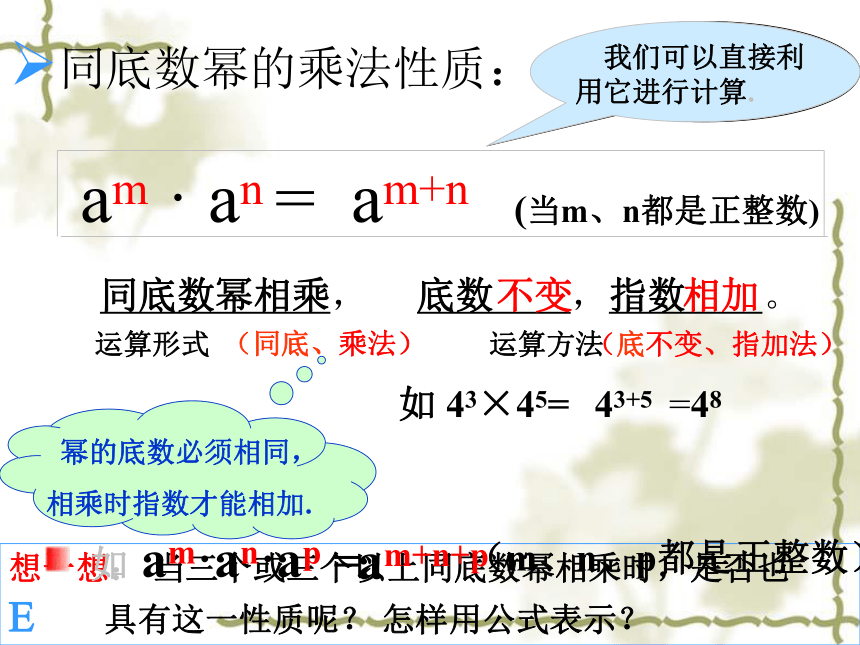
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法性质:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
运算形式
运算方法
(同底、乘法)
(底不变、指加法)
幂的底数必须相同,
相乘时指数才能相加.
例题引领
am · an = am+n (当m、n都是正整数)
am·an·ap = am+n+p (m、n、p都是正整数)
1.计算:
(1)107 ×104 .(2)x2 · x5. (3) a.a6 (4) (-2)6.(-2)8 (5) xm.x2m+1 (6) -26.(-2)8
解:(1)107 ×104 =107 + 4= 1011
(2)x2 · x5 = x2 + 5 = x7
(3) a.a6 =a1+6=a7
(4) (-2)6.(-2)8=(-2)6+8=(-2)14=214
(5) xm.x2m+1 =xm+m+1=x2m+1
(6) -26.(-2)8=-26.28=-26+8=-214
2.计算:
(1)23×24×25 (2)y · y2 · y3
解:(1)23×24×25=23+4+5=212
(2)y · y2 · y3 = y1+2+3=y6
智取百宝箱
1. 计算:(抢答)
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 · a3
(3) x5 · x5
(4) b5 · b
(1) 105×106
Good!
2. 计算:
(1)x10 · x (2)10×102×104
(3)x5 · x · x3 (4)y4· y3· y2· y
解:
(1)x10 · x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 · x · x3 = x5+1+3 = x9
(4)y4 · y3 · y2 · y= y4+3+2+1= y10
3.我是法官我来判
(1)b5 · b5= 2b5 ( )
(2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( )
(4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( )
(6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 · y5 =y10
c · c3 = c4
×
×
×
×
×
×
了不起!
填空:
(1)x5 ·( )=x 8 (2)a ·( )=a6
(3)x · x3( )=x7 (4)xm ·( )=x3m
随机应变
x3
a5
x3
x2m
真棒!
真不错!
你真行!
太棒了!
实际应用
我国陆地面积约是9.6× 平方千米。平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧1.3× 吨煤所产生的能量。求在我国领土上,一年内从太阳得到的能量相当于燃烧多少吨煤所产生的能量。
解:(9.6 ×106) ×(1.3 ×105)
=9.6 ×106 ×1.3 ×105
=9.6 ×1.3 ×106 ×105
=12.48×1011
=1.248×1012(吨)
答:一年内从太阳得到的能量相当于燃烧1.248×1012吨煤所产生的能量。
挑战平台
1.计算: (1)
解:
原式=(-a)1+4+3
=(-a) 8
(2) (x+y)3 · (x+y)4 .
am · an = am+n
解:
(x+y)3 · (x+y)4 =
(x+y)3+4 =(x+y)7
公式中的a可代表一个数、字母、式子等.
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
整理反思
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子 公式 应用
不变,
相加.
快乐套餐:P148习题15.1-1(1).(2),2(1),8
15.1.1 同底数幂的乘法
an 表示的意义是什么?其中a、n、an分 别叫做什么
an
底数
幂
指数
提出问题,创设情景:
an = a × a × a ×… a
n个a
25表示什么?
问题:
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
(乘方的意义)
(乘方的意义)
10×10×10×10×10 可以写成什么形式
式子103×102的意义是什么?
思考:
103与102 的积
底数相同
这个式子中的两个因式有何特点?
请同学们先根据自己的理解,解答下列各题.
103 ×102 =(10×10×10)×(10×10) = 10( )
23 ×22 = =2( )
5
(2×2×2)×(2×2)
5
a3×a2 = = a( ) .
5
(a a a)
(a a)
=2×2×2×2×2
= a a a a a
3个a
2个a
5个a
探究在线:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103 ×102 = 10( )
23 ×22 = 2( )
a3× a2 = a( )
5
5
5
猜想: am · an= (当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确.
3+2
3+2
3+2
= 10( );
= 2( );
= a( ) 。
猜想: am · an= am+n (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法性质:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 43×45=
43+5
=48
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
运算形式
运算方法
(同底、乘法)
(底不变、指加法)
幂的底数必须相同,
相乘时指数才能相加.
例题引领
am · an = am+n (当m、n都是正整数)
am·an·ap = am+n+p (m、n、p都是正整数)
1.计算:
(1)107 ×104 .(2)x2 · x5. (3) a.a6 (4) (-2)6.(-2)8 (5) xm.x2m+1 (6) -26.(-2)8
解:(1)107 ×104 =107 + 4= 1011
(2)x2 · x5 = x2 + 5 = x7
(3) a.a6 =a1+6=a7
(4) (-2)6.(-2)8=(-2)6+8=(-2)14=214
(5) xm.x2m+1 =xm+m+1=x2m+1
(6) -26.(-2)8=-26.28=-26+8=-214
2.计算:
(1)23×24×25 (2)y · y2 · y3
解:(1)23×24×25=23+4+5=212
(2)y · y2 · y3 = y1+2+3=y6
智取百宝箱
1. 计算:(抢答)
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 · a3
(3) x5 · x5
(4) b5 · b
(1) 105×106
Good!
2. 计算:
(1)x10 · x (2)10×102×104
(3)x5 · x · x3 (4)y4· y3· y2· y
解:
(1)x10 · x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 · x · x3 = x5+1+3 = x9
(4)y4 · y3 · y2 · y= y4+3+2+1= y10
3.我是法官我来判
(1)b5 · b5= 2b5 ( )
(2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( )
(4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( )
(6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 · y5 =y10
c · c3 = c4
×
×
×
×
×
×
了不起!
填空:
(1)x5 ·( )=x 8 (2)a ·( )=a6
(3)x · x3( )=x7 (4)xm ·( )=x3m
随机应变
x3
a5
x3
x2m
真棒!
真不错!
你真行!
太棒了!
实际应用
我国陆地面积约是9.6× 平方千米。平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧1.3× 吨煤所产生的能量。求在我国领土上,一年内从太阳得到的能量相当于燃烧多少吨煤所产生的能量。
解:(9.6 ×106) ×(1.3 ×105)
=9.6 ×106 ×1.3 ×105
=9.6 ×1.3 ×106 ×105
=12.48×1011
=1.248×1012(吨)
答:一年内从太阳得到的能量相当于燃烧1.248×1012吨煤所产生的能量。
挑战平台
1.计算: (1)
解:
原式=(-a)1+4+3
=(-a) 8
(2) (x+y)3 · (x+y)4 .
am · an = am+n
解:
(x+y)3 · (x+y)4 =
(x+y)3+4 =(x+y)7
公式中的a可代表一个数、字母、式子等.
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
整理反思
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子 公式 应用
不变,
相加.
快乐套餐:P148习题15.1-1(1).(2),2(1),8
