高中物理必修二 运动的合成与分解课件34张PPT
文档属性
| 名称 | 高中物理必修二 运动的合成与分解课件34张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-07 10:44:09 | ||
图片预览



文档简介
第六章 曲线运动
2、运动的合成与分解
v0
回顾
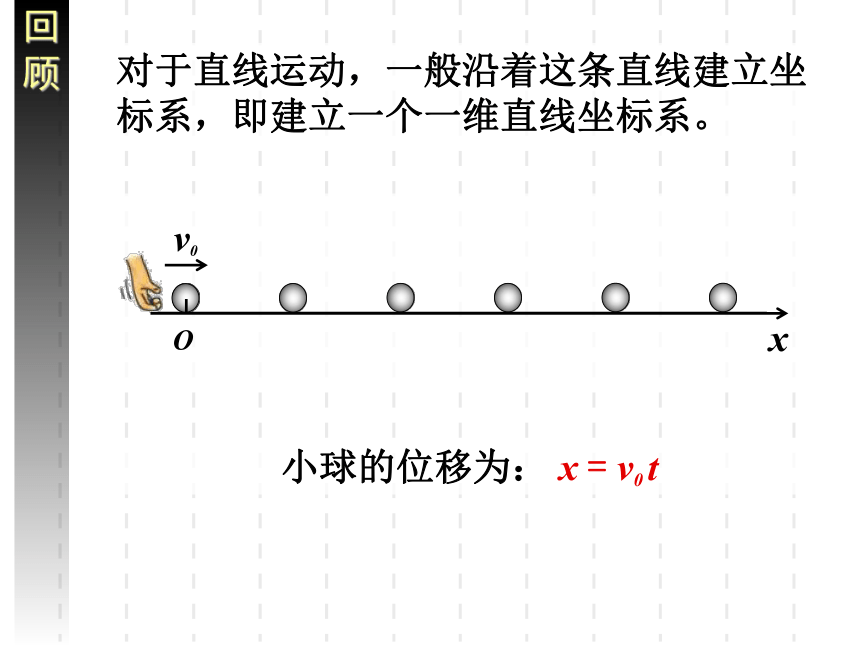
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
小球的位移为: x = v0 t
O
x
回顾
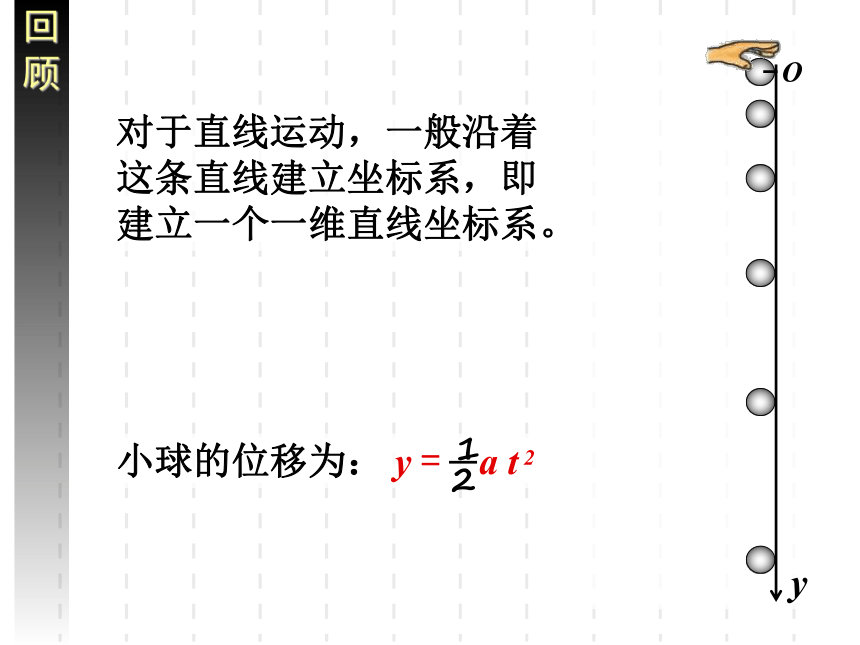
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
O
y
小球的位移为: y = a t 2
1
2
思考
如果物体运动的轨迹不是直线而是曲线,怎样研究、描述这样的曲线运动呢?
建立平面直角坐标系
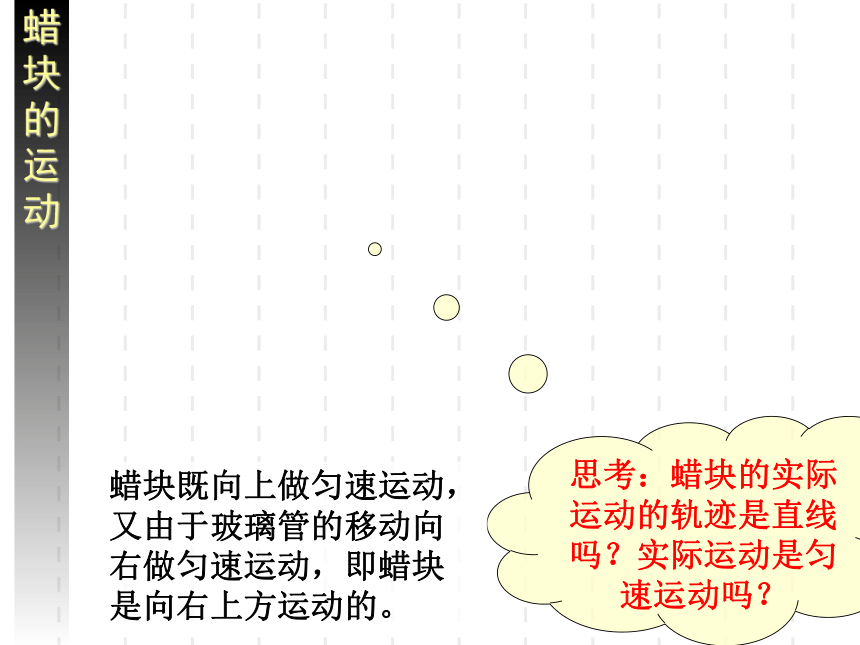
蜡块的运动
思考:蜡块的实际运动的轨迹是直线吗?实际运动是匀速运动吗?
蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
观察红蜡烛的运动情况
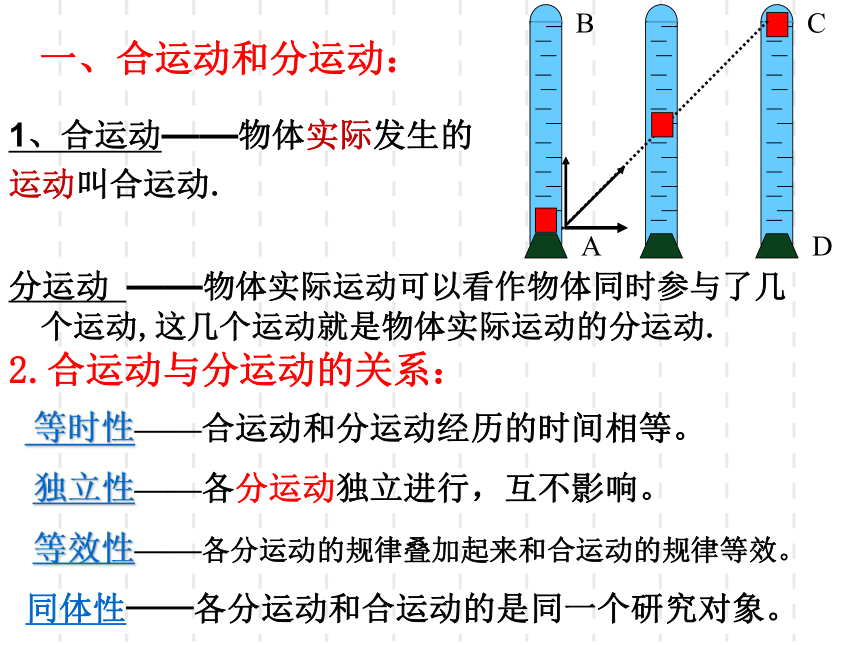
一、合运动和分运动:
2.合运动与分运动的关系:
1、合运动——物体实际发生的
运动叫合运动.
分运动 ——物体实际运动可以看作物体同时参与了几个运动,这几个运动就是物体实际运动的分运动.
等时性——合运动和分运动经历的时间相等。
独立性——各分运动独立进行,互不影响。
等效性——各分运动的规律叠加起来和合运动的规律等效。
同体性——各分运动和合运动的是同一个研究对象。
A
B
D
C
3、运动的合成和分解
已知分运动求合运动, 叫做运动的合成。
已知合运动求分运动, 叫做运动的分解。
(1)定义:
平行四边形定则。
(2)运动的合成和分解所遵循原则:
合运动
A
B
C
D
X
v2
v
v1
C
X1
X2
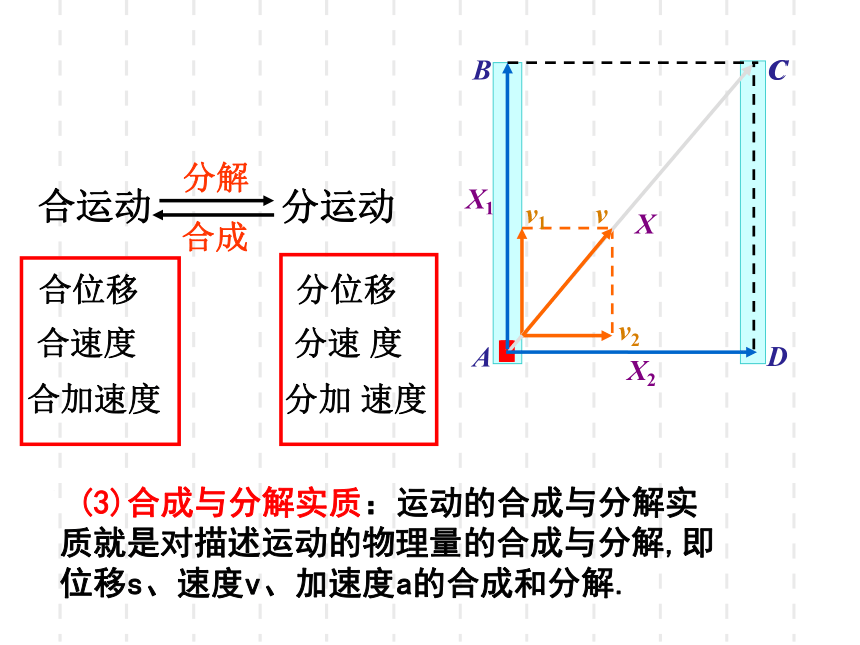
合速度 分速 度
合加速度 分加 速度
分运动
合位移 分位移
分解
合成
(3)合成与分解实质:运动的合成与分解实质就是对描述运动的物理量的合成与分解,即位移s、速度v、加速度a的合成和分解.
a
a1
a2
v1
v2
v
运动的合成与分解
A
B
X
X1
X2
分速度
分速度
合速度
分加速度
合加速度
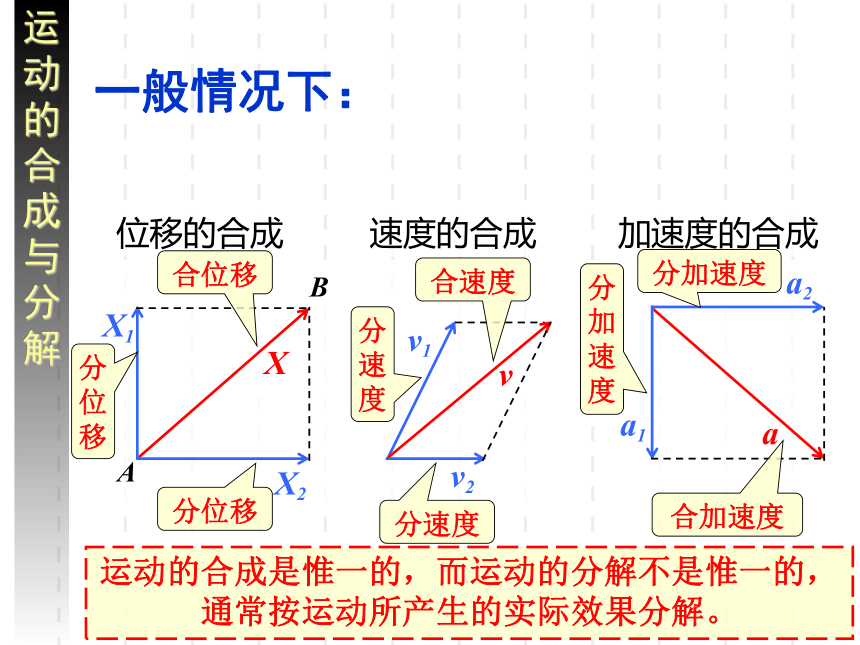
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
一般情况下:
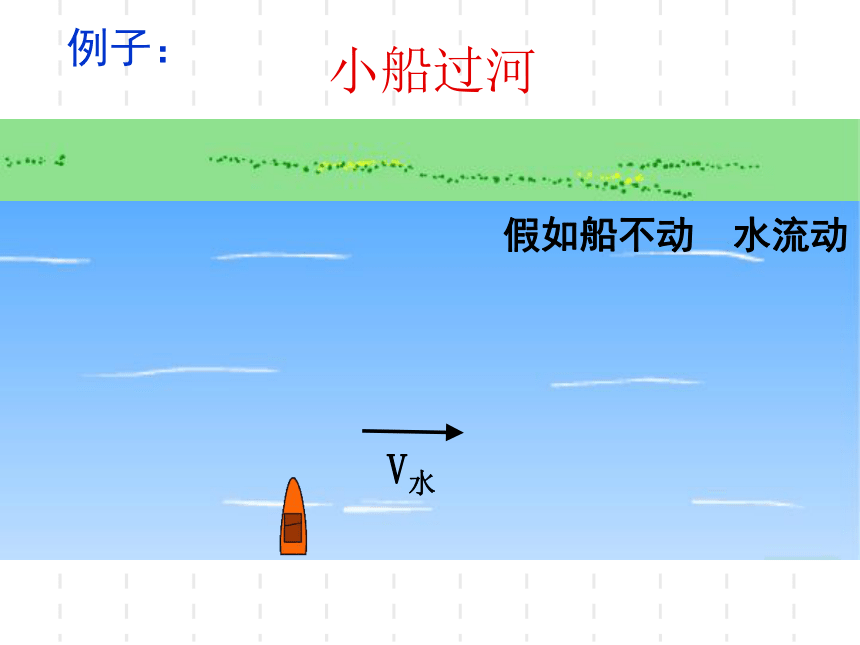
小船过河
假如船不动 水流动
V水
例子:
小船过河
假如水不流动 船动
V船
小船过河问题
V水
V船
小船过河问题
V水
V船
分析:蜡块的轨迹
O
x
y
P
蜡块的位置P 点的坐标
y = x
vx
vy
蜡块的运动轨迹是过原点的一条直线
y = vy t
x = vx t
二、平面坐标系(二维坐标系)研究合运动和分运动
1.蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
O
x
y
P
θ
分析:蜡块的位移、速度
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
思考与讨论
2、如果物体在一个方向上的分运动是匀速直线运动,在与它垂直方向的分运动是匀加速运动,合运动的轨迹是什么样的?
P
x = vx t
物体的位置P 的坐标
y = vy t+ at2
1
2
y = x+ x2
vx
vy
2vx2
a
v
x
y
O
F合
vy
vx
1、两个互成角度的匀速直线运动的合运动
匀速直线运动
2、两个互成角度的匀速直线运动与匀变速直线运动的合运动
匀变速曲线运动
结论:
a1
v1
a1
v1
思考与讨论
?
3、两个互成角度的匀变速直线运动的合运动
①两个初速度为0 的匀加速直线运动
判断几个分运动的合运动,可先把各分运动的合速度以及合加速度求出来,然后根据合速度与合加速度是否在一条直线上加以判断。
②两个初速度不为0 的匀变速直线运动
初速度为0的匀加速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
例:降落伞下落一定时间后的运动是匀速的。没有风的时候,跳伞员着地的速度是4m/s。现在有风,风使他以3m/s的速度沿水平方向东移动,问跳伞员将以多大的速度着地?这个速度的方向怎样?
三、合运动性质和轨迹的判断方法
当加速度a不断变化时,物体做变加速速运动;
(1)、性质的判定
:取决于加速度a;
当加速度a=0时,物体做匀速直线运动;
当加速度a恒定不变时,物体做匀变速运动;
(2)、轨迹的判断:
看合加速度的方向与合初速度的方向是否在一条
直线上:
若在一条直线上,则合运动轨迹是直线;
若不在一条直线上,则合运动轨迹是曲线;
(1)两个互成角度分运动都是匀速直线运动,合运动也是匀速直线运动。
结论: 分运动是直线的运动,其合运动的轨迹可以是直线也可以是曲线。
(2)两个互成角度分运动,一个是匀速直线运动另一个是匀变速直线运动的合运动是曲线运动。
(3)两个互成角度分运动,都是匀变速直线运动的合运动可能是曲线运动,也可能是直线运动。
例如:
四、运动的合成和分解典例
(1)运动的合成典例—小船渡河问题
例、水的流速为5m/s,船在静水中的航速为10m/s,河宽50m,求:
(1)怎样渡河渡河时间最短;
(2)怎样渡河,渡河位移最短;
假如船不动 水流动
V水
水速:水流动的速度。
船速:船在静水中的速度。
船速方向:船头指向的方向。
假如水不流动 船动
V船
船的实际运动方向:水速和船速的合运动方向。
船的实际运动速度大小:水速和船速的矢量和。
V水
V船
小船过河问题
d
x1
x2
x
V
V船
V水
水的流速为5m/s
船在静水中的航速为10m/s
河岸宽50m
求:(1)怎样渡河渡河时间最短
V水
小船过河问题
x1
x2
x
V水
V
V船
θ
水的流速为5m/s,船在静水中的航速为10m/s
河岸宽50m
V水
求:小船过河所用时间
2、运动的分解典例---绳子末端的速度分解
如图所示,用拖车通过绳子把小船拉向湖的岸边,若拖车的速度v恒定不变,试分析在靠岸边过程中,船的速度怎样变化?
v
O
A
将绳子末端的速度一个分解到沿绳方向上,一个分解到垂直于绳方向上;
例、如图2所示,一辆匀速行驶的汽车将一重物提起,在
此过程中,重物A的运动情况是( )
加速上升????
加速上升
C. 减速上升
D. 匀速上升
2、运动的合成与分解
v0
回顾
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
小球的位移为: x = v0 t
O
x
回顾
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
O
y
小球的位移为: y = a t 2
1
2
思考
如果物体运动的轨迹不是直线而是曲线,怎样研究、描述这样的曲线运动呢?
建立平面直角坐标系
蜡块的运动
思考:蜡块的实际运动的轨迹是直线吗?实际运动是匀速运动吗?
蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
观察红蜡烛的运动情况
一、合运动和分运动:
2.合运动与分运动的关系:
1、合运动——物体实际发生的
运动叫合运动.
分运动 ——物体实际运动可以看作物体同时参与了几个运动,这几个运动就是物体实际运动的分运动.
等时性——合运动和分运动经历的时间相等。
独立性——各分运动独立进行,互不影响。
等效性——各分运动的规律叠加起来和合运动的规律等效。
同体性——各分运动和合运动的是同一个研究对象。
A
B
D
C
3、运动的合成和分解
已知分运动求合运动, 叫做运动的合成。
已知合运动求分运动, 叫做运动的分解。
(1)定义:
平行四边形定则。
(2)运动的合成和分解所遵循原则:
合运动
A
B
C
D
X
v2
v
v1
C
X1
X2
合速度 分速 度
合加速度 分加 速度
分运动
合位移 分位移
分解
合成
(3)合成与分解实质:运动的合成与分解实质就是对描述运动的物理量的合成与分解,即位移s、速度v、加速度a的合成和分解.
a
a1
a2
v1
v2
v
运动的合成与分解
A
B
X
X1
X2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
一般情况下:
小船过河
假如船不动 水流动
V水
例子:
小船过河
假如水不流动 船动
V船
小船过河问题
V水
V船
小船过河问题
V水
V船
分析:蜡块的轨迹
O
x
y
P
蜡块的位置P 点的坐标
y = x
vx
vy
蜡块的运动轨迹是过原点的一条直线
y = vy t
x = vx t
二、平面坐标系(二维坐标系)研究合运动和分运动
1.蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
O
x
y
P
θ
分析:蜡块的位移、速度
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
思考与讨论
2、如果物体在一个方向上的分运动是匀速直线运动,在与它垂直方向的分运动是匀加速运动,合运动的轨迹是什么样的?
P
x = vx t
物体的位置P 的坐标
y = vy t+ at2
1
2
y = x+ x2
vx
vy
2vx2
a
v
x
y
O
F合
vy
vx
1、两个互成角度的匀速直线运动的合运动
匀速直线运动
2、两个互成角度的匀速直线运动与匀变速直线运动的合运动
匀变速曲线运动
结论:
a1
v1
a1
v1
思考与讨论
?
3、两个互成角度的匀变速直线运动的合运动
①两个初速度为0 的匀加速直线运动
判断几个分运动的合运动,可先把各分运动的合速度以及合加速度求出来,然后根据合速度与合加速度是否在一条直线上加以判断。
②两个初速度不为0 的匀变速直线运动
初速度为0的匀加速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
例:降落伞下落一定时间后的运动是匀速的。没有风的时候,跳伞员着地的速度是4m/s。现在有风,风使他以3m/s的速度沿水平方向东移动,问跳伞员将以多大的速度着地?这个速度的方向怎样?
三、合运动性质和轨迹的判断方法
当加速度a不断变化时,物体做变加速速运动;
(1)、性质的判定
:取决于加速度a;
当加速度a=0时,物体做匀速直线运动;
当加速度a恒定不变时,物体做匀变速运动;
(2)、轨迹的判断:
看合加速度的方向与合初速度的方向是否在一条
直线上:
若在一条直线上,则合运动轨迹是直线;
若不在一条直线上,则合运动轨迹是曲线;
(1)两个互成角度分运动都是匀速直线运动,合运动也是匀速直线运动。
结论: 分运动是直线的运动,其合运动的轨迹可以是直线也可以是曲线。
(2)两个互成角度分运动,一个是匀速直线运动另一个是匀变速直线运动的合运动是曲线运动。
(3)两个互成角度分运动,都是匀变速直线运动的合运动可能是曲线运动,也可能是直线运动。
例如:
四、运动的合成和分解典例
(1)运动的合成典例—小船渡河问题
例、水的流速为5m/s,船在静水中的航速为10m/s,河宽50m,求:
(1)怎样渡河渡河时间最短;
(2)怎样渡河,渡河位移最短;
假如船不动 水流动
V水
水速:水流动的速度。
船速:船在静水中的速度。
船速方向:船头指向的方向。
假如水不流动 船动
V船
船的实际运动方向:水速和船速的合运动方向。
船的实际运动速度大小:水速和船速的矢量和。
V水
V船
小船过河问题
d
x1
x2
x
V
V船
V水
水的流速为5m/s
船在静水中的航速为10m/s
河岸宽50m
求:(1)怎样渡河渡河时间最短
V水
小船过河问题
x1
x2
x
V水
V
V船
θ
水的流速为5m/s,船在静水中的航速为10m/s
河岸宽50m
V水
求:小船过河所用时间
2、运动的分解典例---绳子末端的速度分解
如图所示,用拖车通过绳子把小船拉向湖的岸边,若拖车的速度v恒定不变,试分析在靠岸边过程中,船的速度怎样变化?
v
O
A
将绳子末端的速度一个分解到沿绳方向上,一个分解到垂直于绳方向上;
例、如图2所示,一辆匀速行驶的汽车将一重物提起,在
此过程中,重物A的运动情况是( )
加速上升????
加速上升
C. 减速上升
D. 匀速上升
