沪科版九年级数学上册21.4二次函数的应用练习题(附答案解析)
文档属性
| 名称 | 沪科版九年级数学上册21.4二次函数的应用练习题(附答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 156.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览




文档简介
初中数学沪科版九年级上册第二十一章21.4二次函数的应用练习题
一、选择题
如图是王阿姨晚饭后步行的路程单位:与时间单位:的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是
A.
,王阿姨步行的路程为800m
B.
线段CD的函数解析式为
C.
,王阿姨步行速度由慢到快
D.
曲线段AB的函数解析式为
二次函数的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使的面积等于的点P共有
A.
1个
B.
2个
C.
3个
D.
4个
某畅销书的售价为每本30元,每星期可卖出200本,书城准备开展“读数节活动”,决定降价促销,经调研,如果调整书籍的售价,每降价2元,每星期可多卖出40本,设每件商品降价x元后,每星期售出此畅销书的总销售额为y元,则y与x之间的函数关系式为
A.
B.
C.
D.
某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为
A.
B.
C.
D.
进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为
A.
B.
C.
D.
为解决药价虚高给老百姓带来的求医难问题,国家决定对药品价格分两次降价,若设平均每次降价的百分率为x,该药品的原价是18元盒,降价后的价格为y元盒,则y与x之间的函数关系式是?
?
A.
B.
C.
D.
在一个边长为2的正方形中挖去一个边长为的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是
A.
B.
C.
D.
矩形的周长为12cm,设其一边长为xcm,面积为,则y与x的函数关系式及其自变量x的取值范围均正确的是
A.
B.
C.
D.
长方形的周长为24cm,其中一边为其中,面积为,则这样的长方形中y与x的关系可以写为??
A.
B.
C.
D.
广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度米关于水珠和喷头的水平距离米的函数解析式是,那么水珠的高度达到最大时,水珠与喷头的水平距离是
A.
1米
B.
2米
C.
5米
D.
6米
二、填空题
某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金元关于x的函数关系式为________.
据权威部门发布的消息,2019年第一季度安徽省城镇居民人均可支配收入约为万元,若第三季度安徽省城镇居民人均可支配收人为y万元,平均每个季度城镇居民人均可支配收入增长的百分率为x,则y与x之间的函数表达式是____.
如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为,设AD的长为,菜园ABCD的面积为,则y关于自变量x的函数关系式是___________________________.
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件,商品进价为每件40元,若设涨价元,总利润为y元,则y与x的函数关系式为______.
某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量万件与x之间的关系应表示为______.
三、解答题
已知抛物线的对称轴为直线,其图象与x轴相交于A,B两点,与y轴相交于点.
求b,c的值;
直线1与x轴相交于点P.
如图1,若轴,且与线段AC及抛物线分别相交于点E,F,点C关于直线的对称点为点D,求四边形CEDF面积的最大值;
如图2,若直线1与线段BC相交于点Q,当∽时,求直线1的表达式.
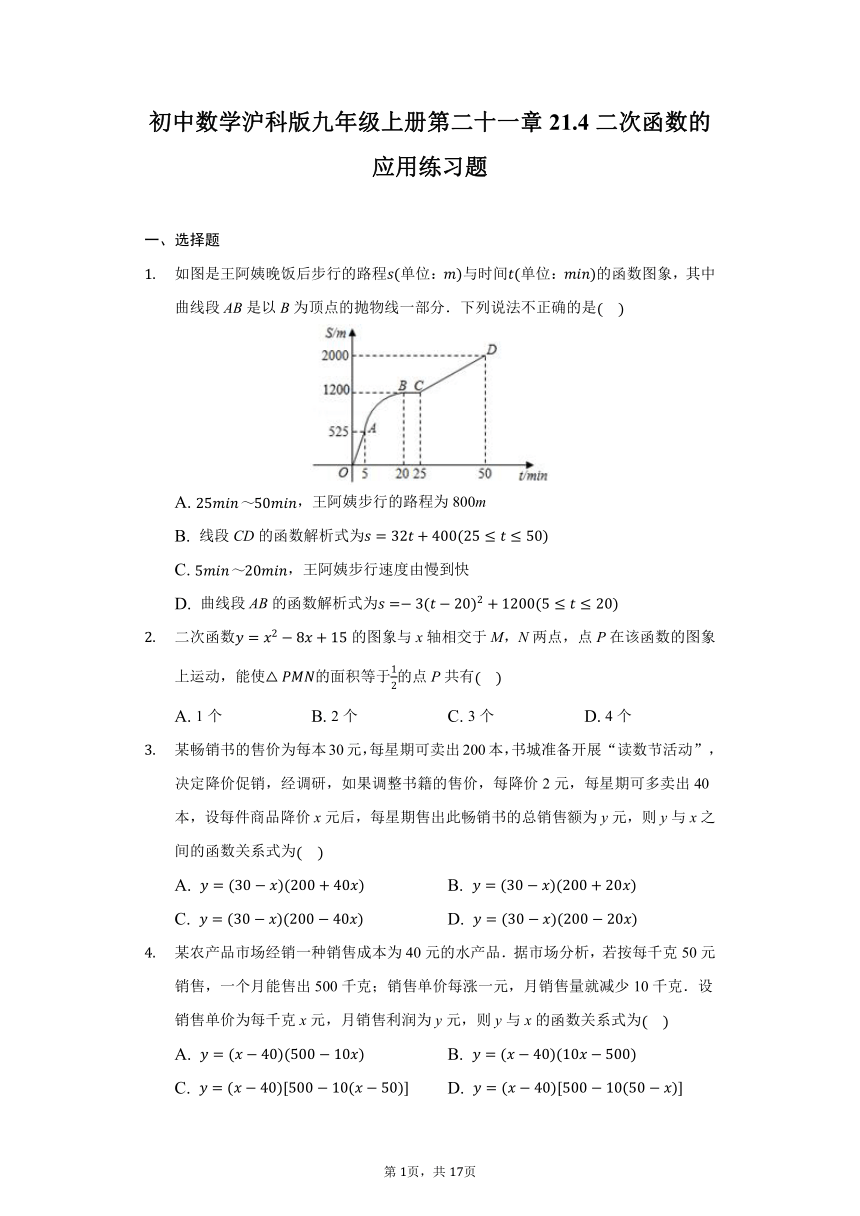
如图1,在平面直角坐标系中,已知抛物线与x轴交于,两点,与y轴交于点C.
求抛物线的函数表达式;
如图2,轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
若点K为抛物线的顶点,点是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
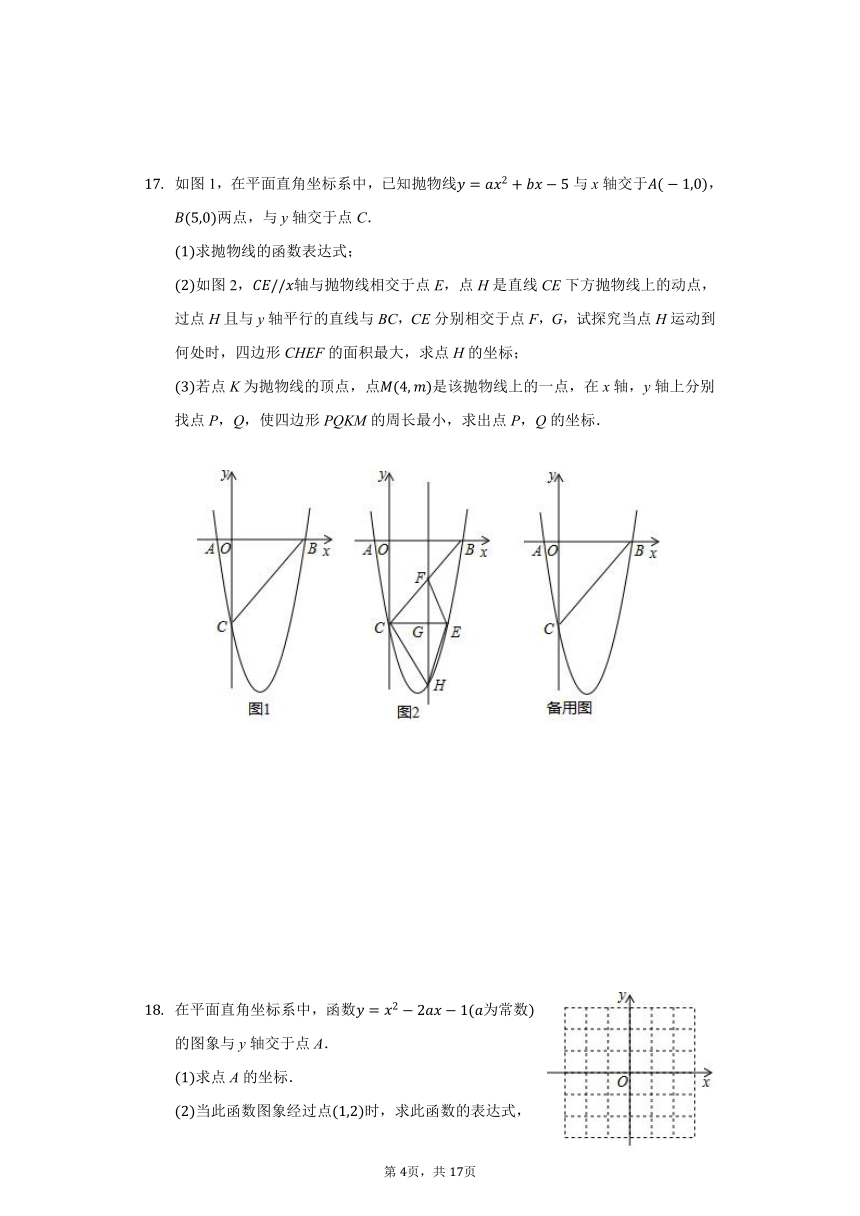
在平面直角坐标系中,函数为常数的图象与y轴交于点A.
求点A的坐标.
当此函数图象经过点时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.
当时,若函数为常数的图象的最低点到直线的距离为2,求a的值.
设,三个顶点的坐标分别为、、当函数为常数的图象与的直角边有交点时,交点记为点过点P作y轴的垂线,与此函数图象的另一个交点为与P不重合,过点A作y轴的垂线,与此函数图象的另一个交点为若,直接写出a的值.
答案和解析
1.【答案】C
【解析】
【分析】
本题考查了二次函数的应用,一次函数的应用,正确的识别图象、数形结合是解题的关键根据函数图象中的信息,利用数形结合求相关线段的解析式解答即可.
【解答】
解:,王阿姨步行的路程为,故A正确;
B.设线段CD的函数解析式为,
把,代入得,,
解得:,
线段CD的函数解析式为,故B正确;
C.在A点的速度为,在B点的速度为,速度从快变慢,故C错误;
D.当,20时,由图象可得,1200m,将,20分别代入得,,故D正确.
故选C.
2.【答案】D
【解析】
【分析】
本题结合图象的性质考查二次函数的综合应用,难度中等.要注意函数求出的各个解是否符合实际.由题可求出MN的长,即的底边已知,要求面积为,那么根据面积即可求出高,只要把相应的y值代入即可解答.
【解答】
解:的图象与x轴交点和,
,
设p点,
,
面积,
可得,或者,
当时,;
当时,,
所以共有四个点.
故选:D.
3.【答案】B
【解析】
【分析】
本题考查由实际问题列二次函数关系式,解答本题的关键是明确题意,列出相应的函数关系式.根据降价x元,则售价为元,销售量为本,由题意可得等量关系:总销售额为销量售价,根据等量关系列出函数解析式即可.
【解答】
解:设每本降价x元,则售价为元,销售量为本,
根据题意得,,
故选B.
4.【答案】C
【解析】
【分析】
此题主要考查了根据实际问题抽象出二次函数关系式,正确表示出销量是解题关键.直接利用每千克利润销量总利润,进而得出关系式.
【解答】
解:设销售单价为每千克x元,月销售利润为y元,
则y与x的函数关系式为:.
故选:C.
5.【答案】D
【解析】解:由题意得第二次降价后的价格是.
则函数解析式是.
故选D.
原价为a,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的,为.
本题需注意第二次降价是在第一次降价后的价格的基础上降价的.
6.【答案】C
【解析】
【分析】
此题主要考查了根据实际问题抽象出二次函数关系式,本题需注意第二次降价是在第一次降价后的价格的基础上降价的.原价为18,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的为:,则函数关系式即可求得.
【解答】
解:原价为18,
第一次降价后的价格是;
第二次降价是在第一次降价后的价格的基础上降价的为:.
则函数解析式是:.
故选C.
7.【答案】B
【解析】解:设剩下部分的面积为y,则:
,
故选:B.
根据剩下部分的面积大正方形的面积小正方形的面积得出y与x的函数关系式即可.
此题主要考查了根据实际问题列二次函数关系式,利用剩下部分的面积大正方形的面积小正方形的面积得出是解题关键.
8.【答案】B
【解析】
【分析】
此题主要考查了根据实际问题列二次函数关系式的知识,解题的关键是用x表示出矩形的另一边,此题难度一般.
已知一边长为xcm,则另一边长为,根据矩形的面积公式即可解答.
【解答】
解:已知一边长为xcm,则另一边长为.
则化简可得,,
故选:B.
9.【答案】C
【解析】
【分析】
本题考查列二次函数关系式,得到长方形的另一边长是解决本题的关键点.
先得到长方形的另一边长,那么面积一边长另一边长.
【解答】
解:长方形的周长为24cm,其中一边为其中,
长方形的另一边长为,
.
故选C.
10.【答案】B
【解析】
【分析】
本题考查了二次函数的应用,解决本题的关键是掌握二次函数的顶点式.根据二次函数的顶点式即可求解.
【解答】
解:方法一:
根据题意,得
,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
方法二:
因为对称轴,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
故选:B.
11.【答案】a
【解析】
【分析】本题考查根据实际问题列二次函数关系式,关键是由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为,而三月份在2月份的基础上又增长了x,那么三月份的研发资金也可以用x表示出来,由此即可确定函数关系式.
【解答】
解:一月份新产品的研发资金为a元,二月份起,每月新产品的研发资金与上月相比增长率都是x,
二月份新产品的研发资金为元,
三月份新产品的研发资金为元,
即.
12.【答案】
【解析】
【分析】
此题主要考查了根据实际问题列二次函数关系式,属于中考常考题型.第一季度安徽省城镇居民人均可支配收入约为万元,第二季度安徽省城镇居民人均可支配收入是元,第三季度安徽省城镇居民人均可支配收人为元,则函数解析式即可求得.
【解答】
解:平均每个季度城镇居民人均可支配收入增长的百分率为x,根据题意可得:
y与x之间的函数关系为:.
故答案为.
13.【答案】
【解析】
【分析】
本题考查了根据实际问题列二次函数关系式、矩形的面积公式的运用,利用篱笆的总长用含x的代数式表示出平行于墙的边长是解题的关键.先用含x的代数式表示出平行于墙的边长,再由矩形的面积公式就可以得出结论;
【解答】
解:根据题意,AD边的长为x米,
则AB边的长为米,
,
即y与x之间的函数关系式为;
,
,
故答案为.
14.【答案】
【解析】解:设涨价元,总利润为y元,
则y与x的函数关系式为:.
故答案为:.
直接利用销量每件利润总利润,进而得出函数关系式.
此题主要考查了根据实际问题列二次函数关系式,正确表示出销量和每件利润是解题关键.
15.【答案】
【解析】解:y与x之间的关系应表示为:.
故答案为:.
根据平均增长问题,可得答案.
本题考查了根据实际问题列二次函数关系式,利用增长问题获得函数解析式是解题关键.
16.【答案】解:由题意得:,
,,
如图1,点C关于直线的对称点为点D,
,
,
解得:,,
,
抛物线的解析式为,
令,解得,,
,,
设直线AC的解析式为,
,解得:,
直线AC的解析式为,
设,,
,
四边形CEDF的面积,
当时,四边形CEDF的面积有最大值,最大值为.
当∽时,
,,
,
,,
,
,
,
如图2,过点P作交AC于点M,
,
设,则,,
,
,
,
,
,
,
设直线l的解析式为,
,
.
直线l的解析式为.
【解析】根据抛物线的对称轴及抛物线与y轴的交点坐标可求出b、c的值;
由题意先求出D点坐标为,求出直线AC的解析式,设,,则,四边形CEDF的面积可表示为,利用二次函数的性质可求出面积的最大值;
当∽时,可得,,则,,过点P作交AC于点M,可求出PM、PA、OP的长,用待定系数法可求出函数解析式.
本题考查了二次函数的综合题:熟练掌握二次函数的性质和轴对称的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,会利用相似三角形的性质解题;要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度是解题的关键.
17.【答案】解:点,在抛物线上,
,
解得,
抛物线的表达式为,
设,
轴,
点E的纵坐标为,
在抛物线上,
,
舍或,
,
,
,,
直线BC的解析式为,
,
,
轴,轴,
,
,
;
如图2,为抛物线的顶点,
,
关于y轴的对称点,
在抛物线上,
,
点M关于x轴的对称点,
直线的解析式为,
,
【解析】根据待定系数法直接确定出抛物线解析式;
先求出直线BC的解析式,进而求出四边形CHEF的面积的函数关系式,即可求出;
利用对称性找出点P,Q的位置,进而求出P,Q的坐标.
此题是二次函数综合题,主要考查了待定系数法,四边形的面积的计算方法,对称性,解的关键是利用对称性找出点P,Q的位置,是一道中等难度的题目.
18.【答案】解:当时,,
点A的坐标为:;
将点代入,
得:,
解得:,
函数的表达式为:,
,
抛物线的开口向上,对称轴为,如图1所示:
当时,y随x的增大而增大;
抛物线的对称轴为:,顶点坐标为:,
当时,对称轴在y轴右侧,如图2所示:
,
最低点就是,
图象的最低点到直线的距离为2,
,
解得:;
当,对称轴在y轴左侧,顶点就是最低点,
如图3所示:
,
整理得:,
解得:,不合题意舍去;
综上所述,a的值为或;
,三个顶点的坐标分别为、、,
直角边为EF与FG,
抛物线的对称轴为:,,
,
当点P在EF边上时,如图4所示:
则,
,
点P在对称轴的左侧,
,
,
,
解得:;
当点P在FG边上时,如图5所示:
则,
,
解得:,,
,
,
,
解得:,不合题意舍去;
综上所述,a的值为或.
【解析】当时,代入,即可得出结果;
将点代入,得,则函数的表达式为,由,得出抛物线的开口向上,对称轴为,则当时,y随x的增大而增大;
抛物线的对称轴为,顶点坐标为,当时,对称轴在y轴右侧,最低点就是,则,即可得出结果;当,对称轴在y轴左侧,顶点就是最低点,则,即可得出结果;
易证直角边为EF与FG,由抛物线的对称轴为,,则,当点P在EF边上时,,则,即可得出结果;当点P在FG边上时,求出,则,即可得出结果.
本题是二次函数综合题,主要考查了二次函数图象与性质、待定系数法求解析式、直角三角形的性质、解一元二次方程、分类讨论等知识;熟练掌握二次函数图象与性质是解题的关键.
第2页,共2页
第1页,共1页
一、选择题
如图是王阿姨晚饭后步行的路程单位:与时间单位:的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是
A.
,王阿姨步行的路程为800m
B.
线段CD的函数解析式为
C.
,王阿姨步行速度由慢到快
D.
曲线段AB的函数解析式为
二次函数的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使的面积等于的点P共有
A.
1个
B.
2个
C.
3个
D.
4个
某畅销书的售价为每本30元,每星期可卖出200本,书城准备开展“读数节活动”,决定降价促销,经调研,如果调整书籍的售价,每降价2元,每星期可多卖出40本,设每件商品降价x元后,每星期售出此畅销书的总销售额为y元,则y与x之间的函数关系式为
A.
B.
C.
D.
某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为
A.
B.
C.
D.
进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为
A.
B.
C.
D.
为解决药价虚高给老百姓带来的求医难问题,国家决定对药品价格分两次降价,若设平均每次降价的百分率为x,该药品的原价是18元盒,降价后的价格为y元盒,则y与x之间的函数关系式是?
?
A.
B.
C.
D.
在一个边长为2的正方形中挖去一个边长为的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是
A.
B.
C.
D.
矩形的周长为12cm,设其一边长为xcm,面积为,则y与x的函数关系式及其自变量x的取值范围均正确的是
A.
B.
C.
D.
长方形的周长为24cm,其中一边为其中,面积为,则这样的长方形中y与x的关系可以写为??
A.
B.
C.
D.
广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度米关于水珠和喷头的水平距离米的函数解析式是,那么水珠的高度达到最大时,水珠与喷头的水平距离是
A.
1米
B.
2米
C.
5米
D.
6米
二、填空题
某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金元关于x的函数关系式为________.
据权威部门发布的消息,2019年第一季度安徽省城镇居民人均可支配收入约为万元,若第三季度安徽省城镇居民人均可支配收人为y万元,平均每个季度城镇居民人均可支配收入增长的百分率为x,则y与x之间的函数表达式是____.
如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为,设AD的长为,菜园ABCD的面积为,则y关于自变量x的函数关系式是___________________________.
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件,商品进价为每件40元,若设涨价元,总利润为y元,则y与x的函数关系式为______.
某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量万件与x之间的关系应表示为______.
三、解答题
已知抛物线的对称轴为直线,其图象与x轴相交于A,B两点,与y轴相交于点.
求b,c的值;
直线1与x轴相交于点P.
如图1,若轴,且与线段AC及抛物线分别相交于点E,F,点C关于直线的对称点为点D,求四边形CEDF面积的最大值;
如图2,若直线1与线段BC相交于点Q,当∽时,求直线1的表达式.
如图1,在平面直角坐标系中,已知抛物线与x轴交于,两点,与y轴交于点C.
求抛物线的函数表达式;
如图2,轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
若点K为抛物线的顶点,点是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
在平面直角坐标系中,函数为常数的图象与y轴交于点A.
求点A的坐标.
当此函数图象经过点时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.
当时,若函数为常数的图象的最低点到直线的距离为2,求a的值.
设,三个顶点的坐标分别为、、当函数为常数的图象与的直角边有交点时,交点记为点过点P作y轴的垂线,与此函数图象的另一个交点为与P不重合,过点A作y轴的垂线,与此函数图象的另一个交点为若,直接写出a的值.
答案和解析
1.【答案】C
【解析】
【分析】
本题考查了二次函数的应用,一次函数的应用,正确的识别图象、数形结合是解题的关键根据函数图象中的信息,利用数形结合求相关线段的解析式解答即可.
【解答】
解:,王阿姨步行的路程为,故A正确;
B.设线段CD的函数解析式为,
把,代入得,,
解得:,
线段CD的函数解析式为,故B正确;
C.在A点的速度为,在B点的速度为,速度从快变慢,故C错误;
D.当,20时,由图象可得,1200m,将,20分别代入得,,故D正确.
故选C.
2.【答案】D
【解析】
【分析】
本题结合图象的性质考查二次函数的综合应用,难度中等.要注意函数求出的各个解是否符合实际.由题可求出MN的长,即的底边已知,要求面积为,那么根据面积即可求出高,只要把相应的y值代入即可解答.
【解答】
解:的图象与x轴交点和,
,
设p点,
,
面积,
可得,或者,
当时,;
当时,,
所以共有四个点.
故选:D.
3.【答案】B
【解析】
【分析】
本题考查由实际问题列二次函数关系式,解答本题的关键是明确题意,列出相应的函数关系式.根据降价x元,则售价为元,销售量为本,由题意可得等量关系:总销售额为销量售价,根据等量关系列出函数解析式即可.
【解答】
解:设每本降价x元,则售价为元,销售量为本,
根据题意得,,
故选B.
4.【答案】C
【解析】
【分析】
此题主要考查了根据实际问题抽象出二次函数关系式,正确表示出销量是解题关键.直接利用每千克利润销量总利润,进而得出关系式.
【解答】
解:设销售单价为每千克x元,月销售利润为y元,
则y与x的函数关系式为:.
故选:C.
5.【答案】D
【解析】解:由题意得第二次降价后的价格是.
则函数解析式是.
故选D.
原价为a,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的,为.
本题需注意第二次降价是在第一次降价后的价格的基础上降价的.
6.【答案】C
【解析】
【分析】
此题主要考查了根据实际问题抽象出二次函数关系式,本题需注意第二次降价是在第一次降价后的价格的基础上降价的.原价为18,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的为:,则函数关系式即可求得.
【解答】
解:原价为18,
第一次降价后的价格是;
第二次降价是在第一次降价后的价格的基础上降价的为:.
则函数解析式是:.
故选C.
7.【答案】B
【解析】解:设剩下部分的面积为y,则:
,
故选:B.
根据剩下部分的面积大正方形的面积小正方形的面积得出y与x的函数关系式即可.
此题主要考查了根据实际问题列二次函数关系式,利用剩下部分的面积大正方形的面积小正方形的面积得出是解题关键.
8.【答案】B
【解析】
【分析】
此题主要考查了根据实际问题列二次函数关系式的知识,解题的关键是用x表示出矩形的另一边,此题难度一般.
已知一边长为xcm,则另一边长为,根据矩形的面积公式即可解答.
【解答】
解:已知一边长为xcm,则另一边长为.
则化简可得,,
故选:B.
9.【答案】C
【解析】
【分析】
本题考查列二次函数关系式,得到长方形的另一边长是解决本题的关键点.
先得到长方形的另一边长,那么面积一边长另一边长.
【解答】
解:长方形的周长为24cm,其中一边为其中,
长方形的另一边长为,
.
故选C.
10.【答案】B
【解析】
【分析】
本题考查了二次函数的应用,解决本题的关键是掌握二次函数的顶点式.根据二次函数的顶点式即可求解.
【解答】
解:方法一:
根据题意,得
,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
方法二:
因为对称轴,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
故选:B.
11.【答案】a
【解析】
【分析】本题考查根据实际问题列二次函数关系式,关键是由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为,而三月份在2月份的基础上又增长了x,那么三月份的研发资金也可以用x表示出来,由此即可确定函数关系式.
【解答】
解:一月份新产品的研发资金为a元,二月份起,每月新产品的研发资金与上月相比增长率都是x,
二月份新产品的研发资金为元,
三月份新产品的研发资金为元,
即.
12.【答案】
【解析】
【分析】
此题主要考查了根据实际问题列二次函数关系式,属于中考常考题型.第一季度安徽省城镇居民人均可支配收入约为万元,第二季度安徽省城镇居民人均可支配收入是元,第三季度安徽省城镇居民人均可支配收人为元,则函数解析式即可求得.
【解答】
解:平均每个季度城镇居民人均可支配收入增长的百分率为x,根据题意可得:
y与x之间的函数关系为:.
故答案为.
13.【答案】
【解析】
【分析】
本题考查了根据实际问题列二次函数关系式、矩形的面积公式的运用,利用篱笆的总长用含x的代数式表示出平行于墙的边长是解题的关键.先用含x的代数式表示出平行于墙的边长,再由矩形的面积公式就可以得出结论;
【解答】
解:根据题意,AD边的长为x米,
则AB边的长为米,
,
即y与x之间的函数关系式为;
,
,
故答案为.
14.【答案】
【解析】解:设涨价元,总利润为y元,
则y与x的函数关系式为:.
故答案为:.
直接利用销量每件利润总利润,进而得出函数关系式.
此题主要考查了根据实际问题列二次函数关系式,正确表示出销量和每件利润是解题关键.
15.【答案】
【解析】解:y与x之间的关系应表示为:.
故答案为:.
根据平均增长问题,可得答案.
本题考查了根据实际问题列二次函数关系式,利用增长问题获得函数解析式是解题关键.
16.【答案】解:由题意得:,
,,
如图1,点C关于直线的对称点为点D,
,
,
解得:,,
,
抛物线的解析式为,
令,解得,,
,,
设直线AC的解析式为,
,解得:,
直线AC的解析式为,
设,,
,
四边形CEDF的面积,
当时,四边形CEDF的面积有最大值,最大值为.
当∽时,
,,
,
,,
,
,
,
如图2,过点P作交AC于点M,
,
设,则,,
,
,
,
,
,
,
设直线l的解析式为,
,
.
直线l的解析式为.
【解析】根据抛物线的对称轴及抛物线与y轴的交点坐标可求出b、c的值;
由题意先求出D点坐标为,求出直线AC的解析式,设,,则,四边形CEDF的面积可表示为,利用二次函数的性质可求出面积的最大值;
当∽时,可得,,则,,过点P作交AC于点M,可求出PM、PA、OP的长,用待定系数法可求出函数解析式.
本题考查了二次函数的综合题:熟练掌握二次函数的性质和轴对称的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,会利用相似三角形的性质解题;要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度是解题的关键.
17.【答案】解:点,在抛物线上,
,
解得,
抛物线的表达式为,
设,
轴,
点E的纵坐标为,
在抛物线上,
,
舍或,
,
,
,,
直线BC的解析式为,
,
,
轴,轴,
,
,
;
如图2,为抛物线的顶点,
,
关于y轴的对称点,
在抛物线上,
,
点M关于x轴的对称点,
直线的解析式为,
,
【解析】根据待定系数法直接确定出抛物线解析式;
先求出直线BC的解析式,进而求出四边形CHEF的面积的函数关系式,即可求出;
利用对称性找出点P,Q的位置,进而求出P,Q的坐标.
此题是二次函数综合题,主要考查了待定系数法,四边形的面积的计算方法,对称性,解的关键是利用对称性找出点P,Q的位置,是一道中等难度的题目.
18.【答案】解:当时,,
点A的坐标为:;
将点代入,
得:,
解得:,
函数的表达式为:,
,
抛物线的开口向上,对称轴为,如图1所示:
当时,y随x的增大而增大;
抛物线的对称轴为:,顶点坐标为:,
当时,对称轴在y轴右侧,如图2所示:
,
最低点就是,
图象的最低点到直线的距离为2,
,
解得:;
当,对称轴在y轴左侧,顶点就是最低点,
如图3所示:
,
整理得:,
解得:,不合题意舍去;
综上所述,a的值为或;
,三个顶点的坐标分别为、、,
直角边为EF与FG,
抛物线的对称轴为:,,
,
当点P在EF边上时,如图4所示:
则,
,
点P在对称轴的左侧,
,
,
,
解得:;
当点P在FG边上时,如图5所示:
则,
,
解得:,,
,
,
,
解得:,不合题意舍去;
综上所述,a的值为或.
【解析】当时,代入,即可得出结果;
将点代入,得,则函数的表达式为,由,得出抛物线的开口向上,对称轴为,则当时,y随x的增大而增大;
抛物线的对称轴为,顶点坐标为,当时,对称轴在y轴右侧,最低点就是,则,即可得出结果;当,对称轴在y轴左侧,顶点就是最低点,则,即可得出结果;
易证直角边为EF与FG,由抛物线的对称轴为,,则,当点P在EF边上时,,则,即可得出结果;当点P在FG边上时,求出,则,即可得出结果.
本题是二次函数综合题,主要考查了二次函数图象与性质、待定系数法求解析式、直角三角形的性质、解一元二次方程、分类讨论等知识;熟练掌握二次函数图象与性质是解题的关键.
第2页,共2页
第1页,共1页
