1.2.4 绝对值课件(共18张PPT)
图片预览






文档简介
(共18张PPT)
1.2.4
绝对值
第二课时
有理数大小的比较
人教版
七年级
教学目标:
1、知识与技能会比较两个(或几个)有理数的大小。
2、过程与方法通过具体实例,抽象出比较两个有理数大小的方法。利用数轴,会比较几个有理数的大小,进一步培养学生数形结合的数学思想方法,提高学生学习兴趣。
重点、难点:
1、重点:
掌握有理数大小的比较法则。
2、难点:
比较两个负数的大小
下图表示某一天我国5个城市的最低气温.
武汉5
℃
北京-10℃ 上海0℃
广州10℃
哈尔滨-20℃
讲授新课
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
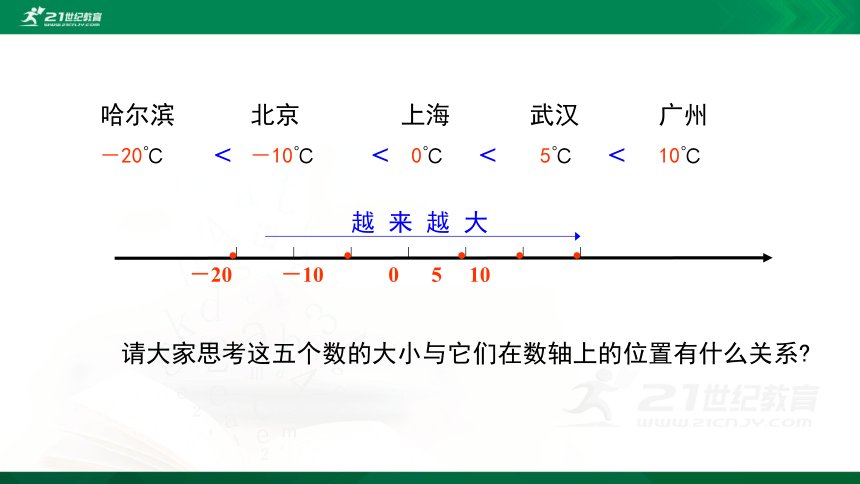
请大家思考这五个数的大小与它们在数轴上的位置有什么关系?
越
来
越
大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20
-10
0
5
10
●
●
●
●
●
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
想一想
有没有最大的有理数?有没有最小的有理数?为什么?
-4
-2
-1
1
2
3
5
●
●
●
●
例1
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5
<-3
<0
<4
典例精析
-5
-3
0
4
运用法则比较有理数的大小
二
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
例如,1
>
0,0
>
-1,1
>
-1,-1
>
-2.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是(
)
A.a>b>c
B.b>c>a
C.c>a>b
D.b>a>c
针对训练
D
例2.
比较下列各数的大小.
解:先化简,-(-1)=1,
-(+2)=-2,
因为正数大于负数,所以1>-2,即
(1)-(-1)和-(+2);
异号两数比较要考虑它们的正负.
-(-1)>-(+2)
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
?
?
解:先化简:
?
?
下列判断,正确的是(
)
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
能力提升
D
×
如a=1,b=-2
×
如a=-3,b=2
×
如a=-3,b=-2
√
当堂练习
2.比较下面各对数的大小,并说明理由:
>
<
>
=
1.在有理数0,│-(-3
)│,-│+1000│,-(-5)中最大的数是(
)
A.0
B.-(-5)
C.-│+1000│
D.│-(-3
)│
B
3.将下列这些数用“<”连接.
0,-3,|5|,-(-4),-|-5|.
解:-|-5|<
-3
<0<
-(-4)<|5|.
4.如果a是有理数,试比较|a|与-2a的大小.
分析:由于不能确定a的正负,所以需分类讨论
解:?当a>0时,|a|>0,-2a<0,所以|a|>-2a;
?当a=0时,|a|=0,-2a=0,所以|a|=-2a;
?当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
课堂小结
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左
边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.2.4
绝对值
第二课时
有理数大小的比较
人教版
七年级
教学目标:
1、知识与技能会比较两个(或几个)有理数的大小。
2、过程与方法通过具体实例,抽象出比较两个有理数大小的方法。利用数轴,会比较几个有理数的大小,进一步培养学生数形结合的数学思想方法,提高学生学习兴趣。
重点、难点:
1、重点:
掌握有理数大小的比较法则。
2、难点:
比较两个负数的大小
下图表示某一天我国5个城市的最低气温.
武汉5
℃
北京-10℃ 上海0℃
广州10℃
哈尔滨-20℃
讲授新课
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
请大家思考这五个数的大小与它们在数轴上的位置有什么关系?
越
来
越
大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20
-10
0
5
10
●
●
●
●
●
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
想一想
有没有最大的有理数?有没有最小的有理数?为什么?
-4
-2
-1
1
2
3
5
●
●
●
●
例1
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5
<-3
<0
<4
典例精析
-5
-3
0
4
运用法则比较有理数的大小
二
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
例如,1
>
0,0
>
-1,1
>
-1,-1
>
-2.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是(
)
A.a>b>c
B.b>c>a
C.c>a>b
D.b>a>c
针对训练
D
例2.
比较下列各数的大小.
解:先化简,-(-1)=1,
-(+2)=-2,
因为正数大于负数,所以1>-2,即
(1)-(-1)和-(+2);
异号两数比较要考虑它们的正负.
-(-1)>-(+2)
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
?
?
解:先化简:
?
?
下列判断,正确的是(
)
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
能力提升
D
×
如a=1,b=-2
×
如a=-3,b=2
×
如a=-3,b=-2
√
当堂练习
2.比较下面各对数的大小,并说明理由:
>
<
>
=
1.在有理数0,│-(-3
)│,-│+1000│,-(-5)中最大的数是(
)
A.0
B.-(-5)
C.-│+1000│
D.│-(-3
)│
B
3.将下列这些数用“<”连接.
0,-3,|5|,-(-4),-|-5|.
解:-|-5|<
-3
<0<
-(-4)<|5|.
4.如果a是有理数,试比较|a|与-2a的大小.
分析:由于不能确定a的正负,所以需分类讨论
解:?当a>0时,|a|>0,-2a<0,所以|a|>-2a;
?当a=0时,|a|=0,-2a=0,所以|a|=-2a;
?当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
课堂小结
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左
边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
