青岛版七年级数学上册单元冲刺卷 第7章 一元一次方程(含答案)
文档属性
| 名称 | 青岛版七年级数学上册单元冲刺卷 第7章 一元一次方程(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 00:00:00 | ||
图片预览


文档简介
第7章 一元一次方程
一、选择题(共11小题;共55分)
1. 已知 x=3 是方程 2x-m=-1 的解,则 m 的值是 ??
A. -7 B. -5 C. 5 D. 7
2. 解方程 x2-1=x-13 时,去分母正确的是 ??
A. 3x-3=2x-2 B. 3x-6=2x-2
C. 3x-6=2x-1 D. 3x-3=2x-1
3. 将方程 2x-1=3x-1 的两边同除以 x-1,则有 2=3,其错误的原因是 ??
A. 方程本身是错的 B. 方程无解
C. 两边都除以 0 D. 2x-1小于3x-1
4. 下列说法错误的是 ??
A. 若 a=b,则 a-3=b-3 B. 若 -3x=-3y,则 x=y
C. 若 a=b,则 ac2+1=bc2+1 D. 若 x2=5x,则 x=5
5. 某个体户在一次买卖中,同时卖出两件上衣,每件上衣以 135 元出售,如果按成本计算,其中一件盈利 25%,另一件亏本 25%,那么在这次买卖中他 ??
A. 不赚不赔 B. 赚了 9 元 C. 赔了 18 元 D. 赚了 18 元
6. 若关于 x 的分式方程 m-1x-1=2 的解为正数,则 m 的取值范围是 ??
A. m>-1 B. m≠1
C. m>1 D. m>-1 且 m≠1
7. x=-2 是下列方程中哪一个方程的解 ??
A. -2x+5=3x+10 B. x2-4=4x
C. xx-2=-4x D. 5x-3=6x-2
8. 下列方程变形一定成立的是 ??
A. 如果 S=12ab ,那么 b=S2a B. 如果 12x=6 ,那么 x=3
C. 如果 x-3=2x-3 ,那么 x=0 D. 如果 mx=my ,那么 x=y
9. 某种商品的标价为 120 元,若以九折降价出售,相对于进货价仍获利 20%,该商品的进货价为 ??
A. 80 元 B. 85 元 C. 90 元 D. 95 元
10. 设"●、■、▲"分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架也平衡,那么"?"处应放"■"的个数为 ??
A. 5 B. 4 C. 3 D. 2
11. 如果 x=y,那么下列各式中正确的是 ??
A. ax-1=ay+1 B. xa=ya C. a-x=a-y D. x-a=y+a
二、填空题(共6小题;共30分)
12. 满足 ∣x-1∣=5 的 x 的值为 ? .
13. 若方程 a-3xa-2-7=0 是一个一元一次方程,则 a 等于 ?.
14. 已知 6-3m+n-52=3m-6-m-3n2,则 m-n= ?.
15. 如果 x=-1 是方程 3kx-2k=8 的解,则 k= ?.
16. 一商场对某款羊毛衫进行换季打折销售,若这款羊毛衫每件按原价的八折(即按照原价的 80%)销售,售价为 120 元,则这款羊毛衫的原销售价为 ? 元.
17. 小华同学在解方程 5x-1= ? x+3 时,把“ ?”处的数字看成了它的相反数,解得 x=2,则该方程的正确解应为 x= ?.
三、解答题(共5小题;共65分)
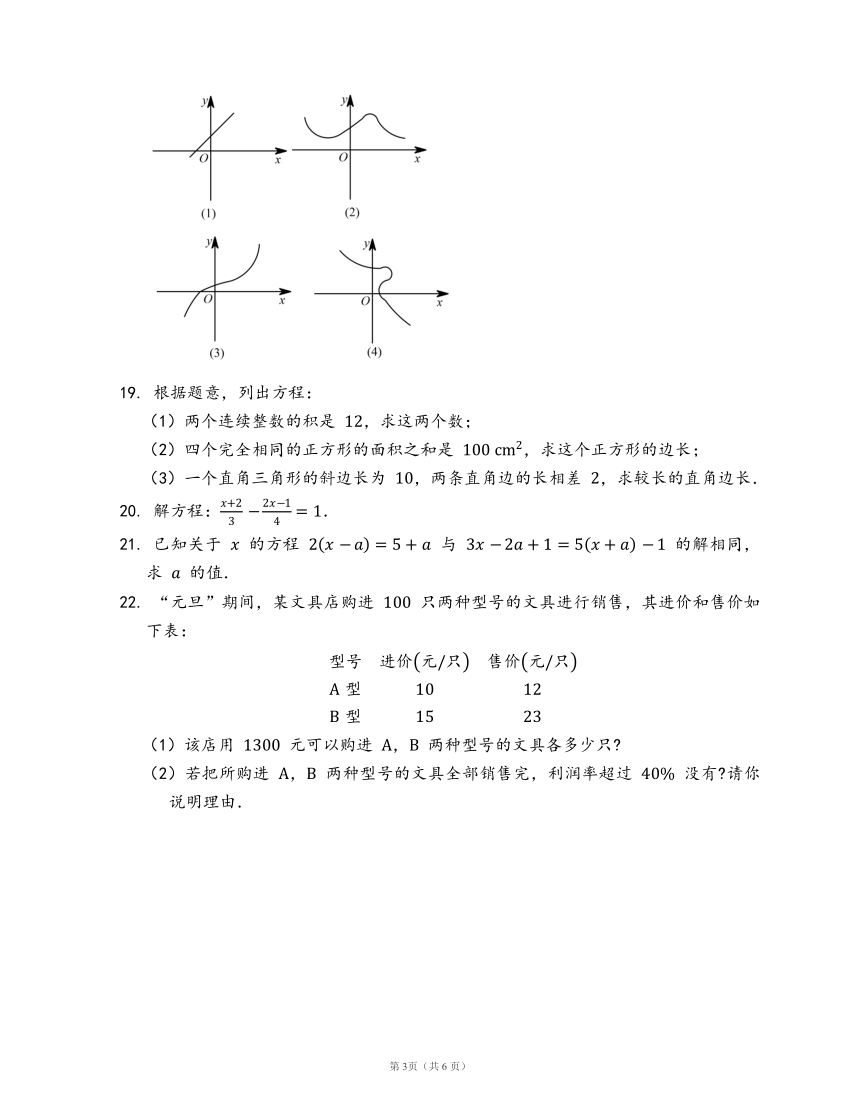
18. 下列各曲线中哪些表示 y 是 x 的函数?
19. 根据题意,列出方程:
(1)两个连续整数的积是 12,求这两个数;
(2)四个完全相同的正方形的面积之和是 100?cm2,求这个正方形的边长;
(3)一个直角三角形的斜边长为 10,两条直角边的长相差 2,求较长的直角边长.
20. 解方程:x+23-2x-14=1.
21. 已知关于 x 的方程 2x-a=5+a 与 3x-2a+1=5x+a-1 的解相同,求 a 的值.
22. “元旦”期间,某文具店购进 100 只两种型号的文具进行销售,其进价和售价如下表:
型号进价元/只售价元/只A型1012B型1523
(1)该店用 1300 元可以购进 A,B 两种型号的文具各多少只?
(2)若把所购进 A,B 两种型号的文具全部销售完,利润率超过 40% 没有?请你说明理由.
答案
第一部分
1. D 【解析】把 x=3 代入方程 2x-m=-1 得:6-m=-1,
解得:m=7.
2. B
3. C
4. D
5. C
【解析】135×2-1351+0.25+1351-0.25=-18,故赔了 18 元.
6. D 【解析】去分母得,m-1=2x-2,解得,x=m+12.
∵ 方程的解是正数,
∴m+12>0,解这个不等式得,m>-1.
∵m=1 时不符合题意,
∴m≠1.则 m 的取值范围是 m>-1 且 m≠1.
7. C
8. C
9. C
10. A
11. C
第二部分
12. 6 或 -4
13. -3
14. -2
【解析】∵ 6-3m+n-52=3m-6-m-3n2,
∴ 6-3m≤0,m-3≥0,
∴ 6-3m=3m-6,m≥3,
∴ 将已知等式化简,得 n-52=-m-3n2,
∴ n-52+m-3n2=0,
∴ n-5=0,m-3=0,
∴ n=5,m=3,则 m-n=3-5=-2.
15. -85
16. 150
17. 12
【解析】设横线处的数字为 a,
根据题意,把 x=2 代入方程得:10-1=-a×2+3,
解得:a=-3,
∴ 横线处的数字是 -3,
即:5x-1=-3x+3,
解得:x=12.
故该方程的正确解应为 x=12.
第三部分
18. 图(1)(2)(3)中 y 是 x 的函数,图(4)中 y 不是 x 的函数.
19. (1) 设这两个数分别为 x,x+1.根据题意,得 xx+1=12 .
??????(2) 设这个正方形的边长为 x?cm.
根据题意,得 4x2=100 .
??????(3) 设较长的直角边长是 x.
根据题意,得 x2+x-22=102 .
20.
x+23-2x-14=1.
则
4x+812-6x-312=1.
所以有
4x+8-6x-3=12.-2x+11=12.-2x=1.x=-12.
21. 方程 2x-a=5+a 的解为 x=3a+52,
方程 3x-2a+1=5x+a-1 的解为 x=2-7a2,
根据题意,得 3a+52=2-7a2,
解得 a=-310.
22. (1) 设可以购进 A 种型号的文具 x 只,则可以购进 B 种型号的文具 100-x 只,根据题意得:
10x+15100-x=1300.
解得:
x=40.
所以 100-x=60.
答:该店用 1300 元可以购进 A 种型号的文具 40 只,B 种型号的文具 60 只.
??????(2) 12-10×40+23-15×60=560(元),
因为 560÷1300×100%≈43.08%>40%,
所以若把所购进 A,B 两种型号的文具全部销售完,利润率超过 40%.
一、选择题(共11小题;共55分)
1. 已知 x=3 是方程 2x-m=-1 的解,则 m 的值是 ??
A. -7 B. -5 C. 5 D. 7
2. 解方程 x2-1=x-13 时,去分母正确的是 ??
A. 3x-3=2x-2 B. 3x-6=2x-2
C. 3x-6=2x-1 D. 3x-3=2x-1
3. 将方程 2x-1=3x-1 的两边同除以 x-1,则有 2=3,其错误的原因是 ??
A. 方程本身是错的 B. 方程无解
C. 两边都除以 0 D. 2x-1小于3x-1
4. 下列说法错误的是 ??
A. 若 a=b,则 a-3=b-3 B. 若 -3x=-3y,则 x=y
C. 若 a=b,则 ac2+1=bc2+1 D. 若 x2=5x,则 x=5
5. 某个体户在一次买卖中,同时卖出两件上衣,每件上衣以 135 元出售,如果按成本计算,其中一件盈利 25%,另一件亏本 25%,那么在这次买卖中他 ??
A. 不赚不赔 B. 赚了 9 元 C. 赔了 18 元 D. 赚了 18 元
6. 若关于 x 的分式方程 m-1x-1=2 的解为正数,则 m 的取值范围是 ??
A. m>-1 B. m≠1
C. m>1 D. m>-1 且 m≠1
7. x=-2 是下列方程中哪一个方程的解 ??
A. -2x+5=3x+10 B. x2-4=4x
C. xx-2=-4x D. 5x-3=6x-2
8. 下列方程变形一定成立的是 ??
A. 如果 S=12ab ,那么 b=S2a B. 如果 12x=6 ,那么 x=3
C. 如果 x-3=2x-3 ,那么 x=0 D. 如果 mx=my ,那么 x=y
9. 某种商品的标价为 120 元,若以九折降价出售,相对于进货价仍获利 20%,该商品的进货价为 ??
A. 80 元 B. 85 元 C. 90 元 D. 95 元
10. 设"●、■、▲"分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架也平衡,那么"?"处应放"■"的个数为 ??
A. 5 B. 4 C. 3 D. 2
11. 如果 x=y,那么下列各式中正确的是 ??
A. ax-1=ay+1 B. xa=ya C. a-x=a-y D. x-a=y+a
二、填空题(共6小题;共30分)
12. 满足 ∣x-1∣=5 的 x 的值为 ? .
13. 若方程 a-3xa-2-7=0 是一个一元一次方程,则 a 等于 ?.
14. 已知 6-3m+n-52=3m-6-m-3n2,则 m-n= ?.
15. 如果 x=-1 是方程 3kx-2k=8 的解,则 k= ?.
16. 一商场对某款羊毛衫进行换季打折销售,若这款羊毛衫每件按原价的八折(即按照原价的 80%)销售,售价为 120 元,则这款羊毛衫的原销售价为 ? 元.
17. 小华同学在解方程 5x-1= ? x+3 时,把“ ?”处的数字看成了它的相反数,解得 x=2,则该方程的正确解应为 x= ?.
三、解答题(共5小题;共65分)
18. 下列各曲线中哪些表示 y 是 x 的函数?
19. 根据题意,列出方程:
(1)两个连续整数的积是 12,求这两个数;
(2)四个完全相同的正方形的面积之和是 100?cm2,求这个正方形的边长;
(3)一个直角三角形的斜边长为 10,两条直角边的长相差 2,求较长的直角边长.
20. 解方程:x+23-2x-14=1.
21. 已知关于 x 的方程 2x-a=5+a 与 3x-2a+1=5x+a-1 的解相同,求 a 的值.
22. “元旦”期间,某文具店购进 100 只两种型号的文具进行销售,其进价和售价如下表:
型号进价元/只售价元/只A型1012B型1523
(1)该店用 1300 元可以购进 A,B 两种型号的文具各多少只?
(2)若把所购进 A,B 两种型号的文具全部销售完,利润率超过 40% 没有?请你说明理由.
答案
第一部分
1. D 【解析】把 x=3 代入方程 2x-m=-1 得:6-m=-1,
解得:m=7.
2. B
3. C
4. D
5. C
【解析】135×2-1351+0.25+1351-0.25=-18,故赔了 18 元.
6. D 【解析】去分母得,m-1=2x-2,解得,x=m+12.
∵ 方程的解是正数,
∴m+12>0,解这个不等式得,m>-1.
∵m=1 时不符合题意,
∴m≠1.则 m 的取值范围是 m>-1 且 m≠1.
7. C
8. C
9. C
10. A
11. C
第二部分
12. 6 或 -4
13. -3
14. -2
【解析】∵ 6-3m+n-52=3m-6-m-3n2,
∴ 6-3m≤0,m-3≥0,
∴ 6-3m=3m-6,m≥3,
∴ 将已知等式化简,得 n-52=-m-3n2,
∴ n-52+m-3n2=0,
∴ n-5=0,m-3=0,
∴ n=5,m=3,则 m-n=3-5=-2.
15. -85
16. 150
17. 12
【解析】设横线处的数字为 a,
根据题意,把 x=2 代入方程得:10-1=-a×2+3,
解得:a=-3,
∴ 横线处的数字是 -3,
即:5x-1=-3x+3,
解得:x=12.
故该方程的正确解应为 x=12.
第三部分
18. 图(1)(2)(3)中 y 是 x 的函数,图(4)中 y 不是 x 的函数.
19. (1) 设这两个数分别为 x,x+1.根据题意,得 xx+1=12 .
??????(2) 设这个正方形的边长为 x?cm.
根据题意,得 4x2=100 .
??????(3) 设较长的直角边长是 x.
根据题意,得 x2+x-22=102 .
20.
x+23-2x-14=1.
则
4x+812-6x-312=1.
所以有
4x+8-6x-3=12.-2x+11=12.-2x=1.x=-12.
21. 方程 2x-a=5+a 的解为 x=3a+52,
方程 3x-2a+1=5x+a-1 的解为 x=2-7a2,
根据题意,得 3a+52=2-7a2,
解得 a=-310.
22. (1) 设可以购进 A 种型号的文具 x 只,则可以购进 B 种型号的文具 100-x 只,根据题意得:
10x+15100-x=1300.
解得:
x=40.
所以 100-x=60.
答:该店用 1300 元可以购进 A 种型号的文具 40 只,B 种型号的文具 60 只.
??????(2) 12-10×40+23-15×60=560(元),
因为 560÷1300×100%≈43.08%>40%,
所以若把所购进 A,B 两种型号的文具全部销售完,利润率超过 40%.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
