青岛版七年级数学上册单元冲刺卷 第1章 基本的几何图形(含答案)
文档属性
| 名称 | 青岛版七年级数学上册单元冲刺卷 第1章 基本的几何图形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 406.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 10:22:22 | ||
图片预览



文档简介
第1章 基本的几何图形
一、选择题(共15小题;共60分)
1. 如图,下列各式中错误的是 ??
A. AB=AD+DB B. CB=AB-AC
C. CD=CB-DB D. AC=CB-DB
2. 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 ??
A. 两点确定一条直线
B. 两点之间线段最短
C. 垂线段最短
D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
3. 高为 2 且底面为正方形的长方体的体积为 32,则长方体的底面边长为 ??
A. 1 B. 2 C. 4 D. 8
4. 已知三边作三角形,用到的基本作图是 ??
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
5. 下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是 ??
A. B.
C. D.
6. 如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是 ??
A. 中 B. 钓 C. 鱼 D. 岛
7. 下列图形中,属于棱柱的是 ??
A. B.
C. D.
8. 已知 A 、 B 、 C,D 依次是直线 AD 上的 4 个不同点,则下列说法正确的是 ??
A. 线段 AD 与线段 BC 是两条相同线段
B. 直线 AD 与直线 BC 是两条不同直线
C. 射线 AD 与射线 BD 是两条相同射线
D. 射线 BC 与射线 BD 是两条不同射线
9. 如果 C 是直线 AB 上一点,线段 AB=9?cm,BC=1?cm,那么 A,C 两点的距离是 ??
A. 8?cm B. 10?cm C. 8?cm 或 10?cm D. 以上都不对
10. 将一边长为 2 的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是 ??
A. 1 B. 32 C. 12 D. 23
11. 某工程队在修建高速公路时,有时需将弯曲的道路改直,下列公理可以说明这样做能缩短路程的是 ??
A. 直线的公理 B. 直线的公理或线段最短公理
C. 线段最短公理 D. 平行公理
12. 如图所示,4 个三角形均为等边三角形,将图形折叠,得到的立体图形是 ??
A. 三棱锥 B. 圆柱 C. 棱锥 D. 六面体
13. 平面上有四点,经过其中的两点画直线最多可画出 ??
A. 三条 B. 四条 C. 五条 D. 六条
14. 如图,AB=12,C 为 AB 的中点,点 D 在线段 AC 上,且 AD:CB=1:3,则 DB 的长度为 ??
A. 4 B. 6 C. 8 D. 10
15. M,N 两点的距离是 20,有一点 P,如果 PM+PN=30,那么下列结论正确的是 ??
A. P 点必在线段 MN 上
B. P 点必在直线 MN 上
C. P 点必在直线 MN 外
D. P 点可能在直线 MN 外,也可能在直线 MN 上
二、填空题(共8小题;共40分)
16. 一个四棱柱有 ? 个顶点,有 ? 条棱,有 ? 个面,它的侧面是 ? 形.
17. 已知圆椎的母线长为 5?cm ,底面半径为 3?cm ,则它的侧面积是 ? cm2 .(结果可保留 π )
18. 已知:如图,B,C 两点把线段 AD 分成 2:4:3 三部分,M 是 AD 的中点,CD=6?cm,则线段 MC 的长为 ?.
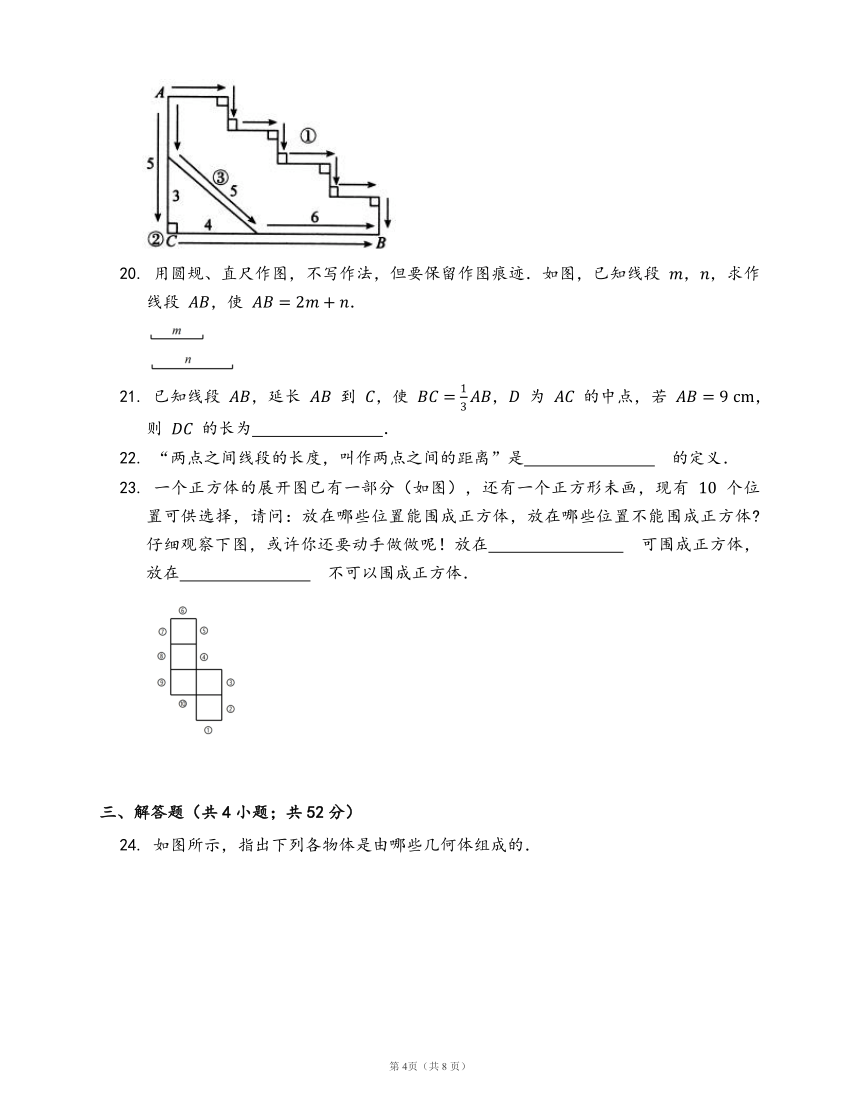
19. 如图所示,从 A 地到 B 地有三条路①②③可走,则第 ? 条路最短,另外两条路的长短关系是 ?.
20. 用圆规、直尺作图,不写作法,但要保留作图痕迹.如图,已知线段 m,n,求作线段 AB,使 AB=2m+n.
21. 已知线段 AB,延长 AB 到 C,使 BC=13AB,D 为 AC 的中点,若 AB=9?cm,则 DC 的长为 ?.
22. “两点之间线段的长度,叫作两点之间的距离”是 ? 的定义.
23. 一个正方体的展开图已有一部分(如图),还有一个正方形未画,现有 10 个位置可供选择,请问:放在哪些位置能围成正方体,放在哪些位置不能围成正方体?仔细观察下图,或许你还要动手做做呢!放在 ? 可围成正方体,放在 ? 不可以围成正方体.
三、解答题(共4小题;共52分)
24. 如图所示,指出下列各物体是由哪些几何体组成的.
25. 如图,有一个正方体的盒子 ABCD-A1B1C1D1,在盒子的顶点 A 处有一只蚂蚁,而在对角的顶点 C1 处有一块糖,蚂蚁应沿着什么路径爬行,才能最快地吃到糖,请画出蚂蚁爬行的路线并简要说明理由.
26. 如图所示,为了给楼梯铺上红地毯,需要计算楼梯的长度.请你设计一种方案,使测量的边数最少,并用字母表示测量的数值,写出需购买的红地毯的长度.
27. 已知:如图,线段 a,b.求作:线段 AC,使 AC=a+b.
答案
第一部分
1. D
2. A
3. C
4. C
5. C
6. C
7. C
8. C
9. C
10. C
【解析】
如图所示,最小的一个面是等腰直角三角形,面积是 12 .
11. C
12. A
13. D
14. D 【解析】∵C 为 AB 的中点,
∴AC=BC=12AB=12×12=6 .
∵AD:CB=1:3,
∴AD=2 .
∴DB=AB-AD=12-2=10.
15. D
第二部分
16. 8,12,6,长方
17. 15π
18. 3?cm
【解析】∵ B,C 两点把线段 AD 分成 2:4:3 三部分,
∴ 设 AB=2x,BC=4x,CD=3x ,
∵ CD=6?cm ,即 3x=6?cm ,解得 x=2?cm ,
∴ AD=2x+4x+3x=9x=9×2=18?cm,
∵ M 是 AD 的中点,
∴ MD=12AD=12×18=9?cm,
∴ MC=MD-CD=9-6=3?cm.
19. ③,相等
20. 如图,线段 AB 即为所求.
21. 6?cm
22. 两点之间的距离
23. ①⑦⑧⑨,②③④⑤⑥⑩
第三部分
24. (1)圆锥、圆柱、正方体;
(2)三棱柱、长方体、圆柱;
(3)球、五棱柱.
25. 经过六种途径可以最快到达,分别取 A1B1,A1D1,BB1,CD,DD1,BC 的中点 P1,P2,P3,P4,P5,P6,六条途径分别为 A-P1-C1,A-P2-C1,A-P3-C1,A-P4-C1,A-P5-C1,A-P6-C1,如图所示,将蚂蚁所在的起始点与终点的平面展开,连接两个目标点,即得到最近线路.
26. ∵A1A+A2B1+A3B2+A4B3+A5B4+A6B5+A7B6+A8B7=BC,
A1B1+A2B2+A3B3+A4B4+A5B5+A6B6+A7B7+A8B=AC,
∴ 只需测量 AC,BC 的长.
设 AC=a,BC=b,
∴ 需购买的红地毯的长度 a+b.
27. 在射线 AM 上顺次截取 AB=a,BC=b.
则线段 AC 就是所求作的线段.
一、选择题(共15小题;共60分)
1. 如图,下列各式中错误的是 ??
A. AB=AD+DB B. CB=AB-AC
C. CD=CB-DB D. AC=CB-DB
2. 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 ??
A. 两点确定一条直线
B. 两点之间线段最短
C. 垂线段最短
D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
3. 高为 2 且底面为正方形的长方体的体积为 32,则长方体的底面边长为 ??
A. 1 B. 2 C. 4 D. 8
4. 已知三边作三角形,用到的基本作图是 ??
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
5. 下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是 ??
A. B.
C. D.
6. 如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是 ??
A. 中 B. 钓 C. 鱼 D. 岛
7. 下列图形中,属于棱柱的是 ??
A. B.
C. D.
8. 已知 A 、 B 、 C,D 依次是直线 AD 上的 4 个不同点,则下列说法正确的是 ??
A. 线段 AD 与线段 BC 是两条相同线段
B. 直线 AD 与直线 BC 是两条不同直线
C. 射线 AD 与射线 BD 是两条相同射线
D. 射线 BC 与射线 BD 是两条不同射线
9. 如果 C 是直线 AB 上一点,线段 AB=9?cm,BC=1?cm,那么 A,C 两点的距离是 ??
A. 8?cm B. 10?cm C. 8?cm 或 10?cm D. 以上都不对
10. 将一边长为 2 的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是 ??
A. 1 B. 32 C. 12 D. 23
11. 某工程队在修建高速公路时,有时需将弯曲的道路改直,下列公理可以说明这样做能缩短路程的是 ??
A. 直线的公理 B. 直线的公理或线段最短公理
C. 线段最短公理 D. 平行公理
12. 如图所示,4 个三角形均为等边三角形,将图形折叠,得到的立体图形是 ??
A. 三棱锥 B. 圆柱 C. 棱锥 D. 六面体
13. 平面上有四点,经过其中的两点画直线最多可画出 ??
A. 三条 B. 四条 C. 五条 D. 六条
14. 如图,AB=12,C 为 AB 的中点,点 D 在线段 AC 上,且 AD:CB=1:3,则 DB 的长度为 ??
A. 4 B. 6 C. 8 D. 10
15. M,N 两点的距离是 20,有一点 P,如果 PM+PN=30,那么下列结论正确的是 ??
A. P 点必在线段 MN 上
B. P 点必在直线 MN 上
C. P 点必在直线 MN 外
D. P 点可能在直线 MN 外,也可能在直线 MN 上
二、填空题(共8小题;共40分)
16. 一个四棱柱有 ? 个顶点,有 ? 条棱,有 ? 个面,它的侧面是 ? 形.
17. 已知圆椎的母线长为 5?cm ,底面半径为 3?cm ,则它的侧面积是 ? cm2 .(结果可保留 π )
18. 已知:如图,B,C 两点把线段 AD 分成 2:4:3 三部分,M 是 AD 的中点,CD=6?cm,则线段 MC 的长为 ?.
19. 如图所示,从 A 地到 B 地有三条路①②③可走,则第 ? 条路最短,另外两条路的长短关系是 ?.
20. 用圆规、直尺作图,不写作法,但要保留作图痕迹.如图,已知线段 m,n,求作线段 AB,使 AB=2m+n.
21. 已知线段 AB,延长 AB 到 C,使 BC=13AB,D 为 AC 的中点,若 AB=9?cm,则 DC 的长为 ?.
22. “两点之间线段的长度,叫作两点之间的距离”是 ? 的定义.
23. 一个正方体的展开图已有一部分(如图),还有一个正方形未画,现有 10 个位置可供选择,请问:放在哪些位置能围成正方体,放在哪些位置不能围成正方体?仔细观察下图,或许你还要动手做做呢!放在 ? 可围成正方体,放在 ? 不可以围成正方体.
三、解答题(共4小题;共52分)
24. 如图所示,指出下列各物体是由哪些几何体组成的.
25. 如图,有一个正方体的盒子 ABCD-A1B1C1D1,在盒子的顶点 A 处有一只蚂蚁,而在对角的顶点 C1 处有一块糖,蚂蚁应沿着什么路径爬行,才能最快地吃到糖,请画出蚂蚁爬行的路线并简要说明理由.
26. 如图所示,为了给楼梯铺上红地毯,需要计算楼梯的长度.请你设计一种方案,使测量的边数最少,并用字母表示测量的数值,写出需购买的红地毯的长度.
27. 已知:如图,线段 a,b.求作:线段 AC,使 AC=a+b.
答案
第一部分
1. D
2. A
3. C
4. C
5. C
6. C
7. C
8. C
9. C
10. C
【解析】
如图所示,最小的一个面是等腰直角三角形,面积是 12 .
11. C
12. A
13. D
14. D 【解析】∵C 为 AB 的中点,
∴AC=BC=12AB=12×12=6 .
∵AD:CB=1:3,
∴AD=2 .
∴DB=AB-AD=12-2=10.
15. D
第二部分
16. 8,12,6,长方
17. 15π
18. 3?cm
【解析】∵ B,C 两点把线段 AD 分成 2:4:3 三部分,
∴ 设 AB=2x,BC=4x,CD=3x ,
∵ CD=6?cm ,即 3x=6?cm ,解得 x=2?cm ,
∴ AD=2x+4x+3x=9x=9×2=18?cm,
∵ M 是 AD 的中点,
∴ MD=12AD=12×18=9?cm,
∴ MC=MD-CD=9-6=3?cm.
19. ③,相等
20. 如图,线段 AB 即为所求.
21. 6?cm
22. 两点之间的距离
23. ①⑦⑧⑨,②③④⑤⑥⑩
第三部分
24. (1)圆锥、圆柱、正方体;
(2)三棱柱、长方体、圆柱;
(3)球、五棱柱.
25. 经过六种途径可以最快到达,分别取 A1B1,A1D1,BB1,CD,DD1,BC 的中点 P1,P2,P3,P4,P5,P6,六条途径分别为 A-P1-C1,A-P2-C1,A-P3-C1,A-P4-C1,A-P5-C1,A-P6-C1,如图所示,将蚂蚁所在的起始点与终点的平面展开,连接两个目标点,即得到最近线路.
26. ∵A1A+A2B1+A3B2+A4B3+A5B4+A6B5+A7B6+A8B7=BC,
A1B1+A2B2+A3B3+A4B4+A5B5+A6B6+A7B7+A8B=AC,
∴ 只需测量 AC,BC 的长.
设 AC=a,BC=b,
∴ 需购买的红地毯的长度 a+b.
27. 在射线 AM 上顺次截取 AB=a,BC=b.
则线段 AC 就是所求作的线段.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
