北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课件(共23张)
文档属性
| 名称 | 北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课件(共23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 23:43:40 | ||
图片预览






文档简介
北师大版数学七年级上册
第5章 一元一次方程
5.3 应用一元一次方程
———水箱变高了
【学习目标】
1.通过分析几何问题中的数量关系,建立方程解决问题.
2.进一步体会运用方程解决问题的关键是找出等量关系.
【学习重点】
分析图形问题中的数量关系,熟练地列方程解应用题.
【学习难点】
从实际问题中抽象出数学模型的教学过程.
学习目标
钢铁工人正在锻造车间工作
导入新知
因此,高变成了 厘米
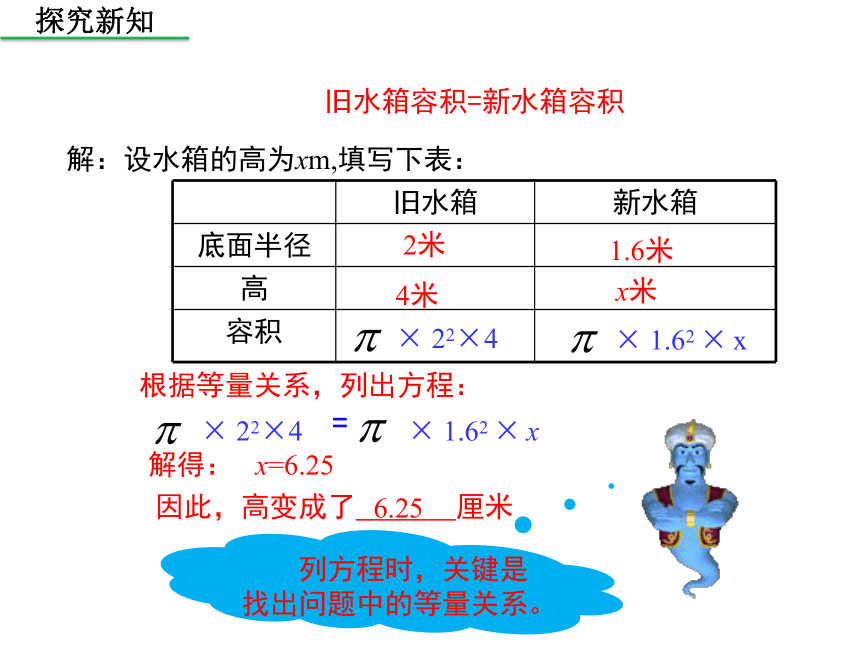
解:设水箱的高为xm,填写下表:
旧水箱
新水箱
底面半径
高
容积
2米
1.6米
4米
x米
× 22×4
旧水箱容积=新水箱容积
× 1.62 × x
根据等量关系,列出方程:
解得: x=6.25
6.25
列方程时,关键是找出问题中的等量关系。
× 22×4
× 1.62 × x
=
探究新知
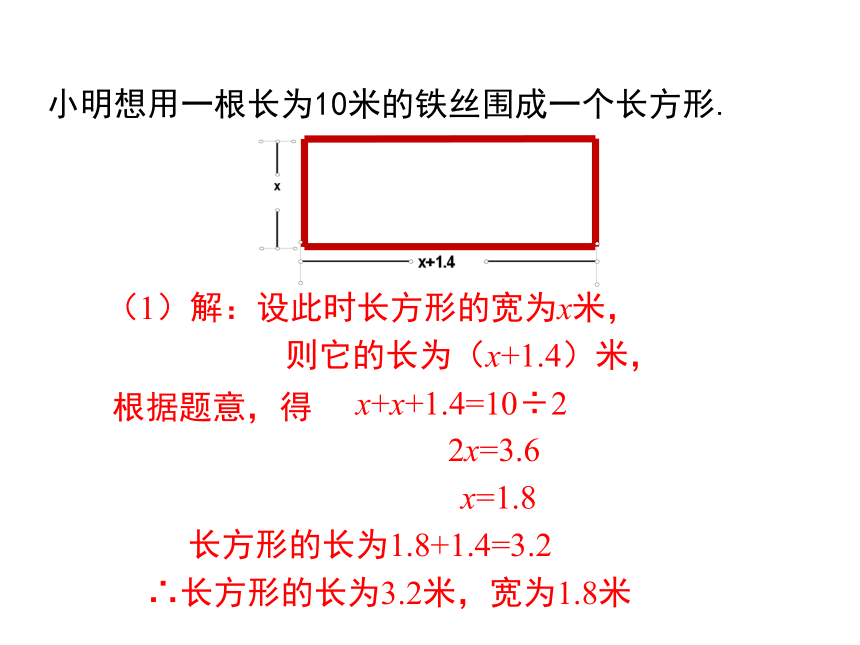
小明想用一根长为10米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
小明
小明想用一根长为10米的铁丝围成一个长方形.
(1)解:设此时长方形的宽为x米,
x+x+1.4=10÷2
2x=3.6
x=1.8
长方形的长为1.8+1.4=3.2
∴长方形的长为3.2米,宽为1.8米
则它的长为(x+1.4)米,
根据题意,得
解:设此时长方形的宽为x米,
x+x+0.8=10÷2
2x=4.2
x=2.1
长方形的长2.1+0.8=2.9
则它的长为(x+0.8)米,
根据题意,得
∴长方形的长为2.9米,宽为2.1米,
S=2.9×2.1=6.09米2,
(1)中的长方形围成的面积:3.2×1.8=5.76米2
比(1)中面积增大6..09-5.76=0.33米2
x
x+0.8
小明想用一根长为10米的铁丝围成一个长方形.
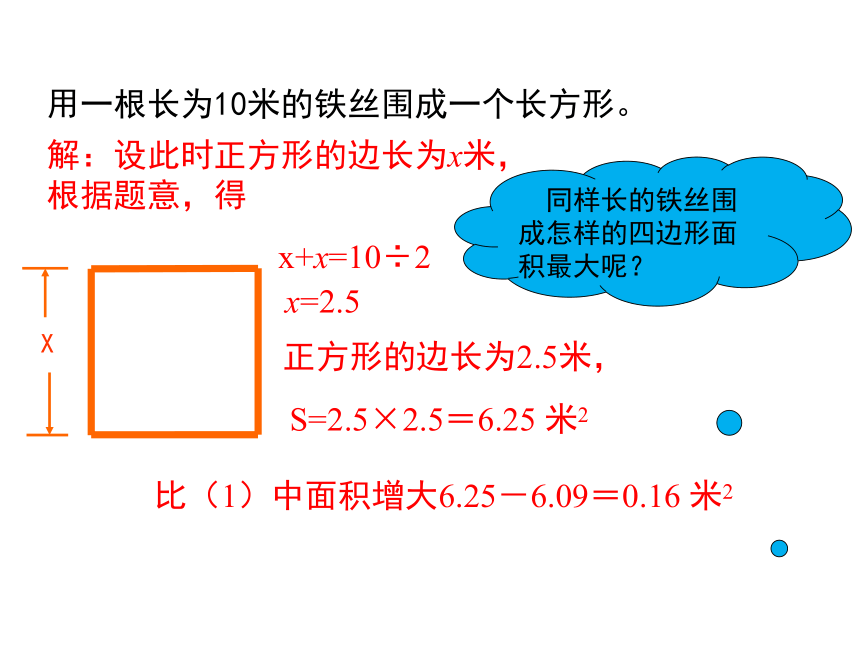
用一根长为10米的铁丝围成一个长方形。
解:设此时正方形的边长为x米,根据题意,得
x+x=10÷2
x=2.5
比(1)中面积增大6.25-6.09=0.16 米2
X
正方形的边长为2.5米,
S=2.5×2.5=6.25 米2
同样长的铁丝围成怎样的四边形面积最大呢?
面积:1.8 × 3.2=5.76
面积:
2.9 ×2.1=6.09
面积:
2.5 × 2.5 =6. 25
围成正方形时面积最大
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示。小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示。小颖所钉长方形的长、宽各为多少厘米?
6
6
10
10
10
10
分析:等量关系是 变形前后周长相等
解:设长方形的长是 x 厘米。
则
解得
因此,小影所钉长方形的长是16厘米,宽是10厘米。
6
6
10
10
10
10
1.把一个用铁丝围成的长方形改制成一个正方形,则这个正方形与原来的长方形比较( )
A.面积与周长都不变化
B.面积相等但周长发生变化
C.周长相等但面积发生变化
D.面积与周长都发生变化
解析:由将一个长方形改制成一个正方形,得出周长没变,但面积发生了变化.故选C.
C
课堂练习
2.内径长为300 mm,内高为32 mm的圆柱形玻璃杯内盛满水,将它里边的水倒入内径长为120 mm的圆柱形玻璃杯,刚好倒满,则内径长为120 mm的玻璃杯的内高为( )
A.150 mm B.200 mm
C.250 mm D.300 mm
B
解析:根据题意知,两个玻璃杯的体积相等.设内径长为120 mm的玻璃杯的内高为x mm.依题意,得π×( )2×32=π×( )2·x,解得x=200.所以内径长为120 mm的玻璃杯的内高为200 mm.故选B.
?
?
3.用一根长为24 cm的铁丝围成一个长与宽的比是2∶1的长方形,则长方形的面积是( )
A.32 cm2 B.36 cm2
C.144 cm2 D.以上都不对
解析:设长方形的宽为x cm,则长为2x cm.根据题意,得2(2x+x)=24,解得x=4,则2x=8,故长方形的面积是4×8=32(cm2).故选A.
A
4.某工厂要制造直径长为120 mm,高为20 mm的圆钢毛坯,现有的原料是直径长为60 mm的圆钢若干米,则应取原料的长为( )
A.50 mm B.60 mm
C.70 mm D.80 mm
D
解析:根据制造前、后的体积相等,所取原料的长相当于立起来时的高.设所取原料的长为x mm.依题意,得π×( )2×20=
π×( )2x,解得x=80.所以所取原料的长为80 mm.故选D.
?
?
5.有一个底面半径长为10 cm,高为30 cm的圆柱形大杯中存满了水,把它里边的水倒入一个底面直径长为10 cm的圆柱形小杯中,刚好倒满12杯,则小杯的高为 ____cm.
10
解析:倒入前、后水的体积相等.设圆柱形小杯的高为x cm.依题意可得π×102×30=π×( )2x×12,解得x=10.
?
6.如图,将一个底面直径长是20厘米,高为9厘米的“矮胖”形圆柱,锻压成底面直径长是10厘米的“瘦高”形圆柱,此时高变成了多少?
解:设此时高变成了x厘米.
根据题意,得π×( )2×9=π×( )2x.
解得x=36.
答:此时高变成了36厘米.
?
?
1、通过体会几何问题中的数量关系的问题情境,体会不变的量-----圆柱的体积、长方形的周长等。
2、通过对实物的具体操作,找出问题中的数量关系并用字母表示它们;
3、通过交流、讨论,根据不变量确定等量关系,列出方程并正确求解。
归纳新知
再 见
第5章 一元一次方程
5.3 应用一元一次方程
———水箱变高了
【学习目标】
1.通过分析几何问题中的数量关系,建立方程解决问题.
2.进一步体会运用方程解决问题的关键是找出等量关系.
【学习重点】
分析图形问题中的数量关系,熟练地列方程解应用题.
【学习难点】
从实际问题中抽象出数学模型的教学过程.
学习目标
钢铁工人正在锻造车间工作
导入新知
因此,高变成了 厘米
解:设水箱的高为xm,填写下表:
旧水箱
新水箱
底面半径
高
容积
2米
1.6米
4米
x米
× 22×4
旧水箱容积=新水箱容积
× 1.62 × x
根据等量关系,列出方程:
解得: x=6.25
6.25
列方程时,关键是找出问题中的等量关系。
× 22×4
× 1.62 × x
=
探究新知
小明想用一根长为10米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
小明
小明想用一根长为10米的铁丝围成一个长方形.
(1)解:设此时长方形的宽为x米,
x+x+1.4=10÷2
2x=3.6
x=1.8
长方形的长为1.8+1.4=3.2
∴长方形的长为3.2米,宽为1.8米
则它的长为(x+1.4)米,
根据题意,得
解:设此时长方形的宽为x米,
x+x+0.8=10÷2
2x=4.2
x=2.1
长方形的长2.1+0.8=2.9
则它的长为(x+0.8)米,
根据题意,得
∴长方形的长为2.9米,宽为2.1米,
S=2.9×2.1=6.09米2,
(1)中的长方形围成的面积:3.2×1.8=5.76米2
比(1)中面积增大6..09-5.76=0.33米2
x
x+0.8
小明想用一根长为10米的铁丝围成一个长方形.
用一根长为10米的铁丝围成一个长方形。
解:设此时正方形的边长为x米,根据题意,得
x+x=10÷2
x=2.5
比(1)中面积增大6.25-6.09=0.16 米2
X
正方形的边长为2.5米,
S=2.5×2.5=6.25 米2
同样长的铁丝围成怎样的四边形面积最大呢?
面积:1.8 × 3.2=5.76
面积:
2.9 ×2.1=6.09
面积:
2.5 × 2.5 =6. 25
围成正方形时面积最大
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示。小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示。小颖所钉长方形的长、宽各为多少厘米?
6
6
10
10
10
10
分析:等量关系是 变形前后周长相等
解:设长方形的长是 x 厘米。
则
解得
因此,小影所钉长方形的长是16厘米,宽是10厘米。
6
6
10
10
10
10
1.把一个用铁丝围成的长方形改制成一个正方形,则这个正方形与原来的长方形比较( )
A.面积与周长都不变化
B.面积相等但周长发生变化
C.周长相等但面积发生变化
D.面积与周长都发生变化
解析:由将一个长方形改制成一个正方形,得出周长没变,但面积发生了变化.故选C.
C
课堂练习
2.内径长为300 mm,内高为32 mm的圆柱形玻璃杯内盛满水,将它里边的水倒入内径长为120 mm的圆柱形玻璃杯,刚好倒满,则内径长为120 mm的玻璃杯的内高为( )
A.150 mm B.200 mm
C.250 mm D.300 mm
B
解析:根据题意知,两个玻璃杯的体积相等.设内径长为120 mm的玻璃杯的内高为x mm.依题意,得π×( )2×32=π×( )2·x,解得x=200.所以内径长为120 mm的玻璃杯的内高为200 mm.故选B.
?
?
3.用一根长为24 cm的铁丝围成一个长与宽的比是2∶1的长方形,则长方形的面积是( )
A.32 cm2 B.36 cm2
C.144 cm2 D.以上都不对
解析:设长方形的宽为x cm,则长为2x cm.根据题意,得2(2x+x)=24,解得x=4,则2x=8,故长方形的面积是4×8=32(cm2).故选A.
A
4.某工厂要制造直径长为120 mm,高为20 mm的圆钢毛坯,现有的原料是直径长为60 mm的圆钢若干米,则应取原料的长为( )
A.50 mm B.60 mm
C.70 mm D.80 mm
D
解析:根据制造前、后的体积相等,所取原料的长相当于立起来时的高.设所取原料的长为x mm.依题意,得π×( )2×20=
π×( )2x,解得x=80.所以所取原料的长为80 mm.故选D.
?
?
5.有一个底面半径长为10 cm,高为30 cm的圆柱形大杯中存满了水,把它里边的水倒入一个底面直径长为10 cm的圆柱形小杯中,刚好倒满12杯,则小杯的高为 ____cm.
10
解析:倒入前、后水的体积相等.设圆柱形小杯的高为x cm.依题意可得π×102×30=π×( )2x×12,解得x=10.
?
6.如图,将一个底面直径长是20厘米,高为9厘米的“矮胖”形圆柱,锻压成底面直径长是10厘米的“瘦高”形圆柱,此时高变成了多少?
解:设此时高变成了x厘米.
根据题意,得π×( )2×9=π×( )2x.
解得x=36.
答:此时高变成了36厘米.
?
?
1、通过体会几何问题中的数量关系的问题情境,体会不变的量-----圆柱的体积、长方形的周长等。
2、通过对实物的具体操作,找出问题中的数量关系并用字母表示它们;
3、通过交流、讨论,根据不变量确定等量关系,列出方程并正确求解。
归纳新知
再 见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
