11.3 角的平分线的性质(一)
文档属性
| 名称 | 11.3 角的平分线的性质(一) |  | |
| 格式 | zip | ||
| 文件大小 | 92.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-23 09:09:56 | ||
图片预览

文档简介
(共14张PPT)
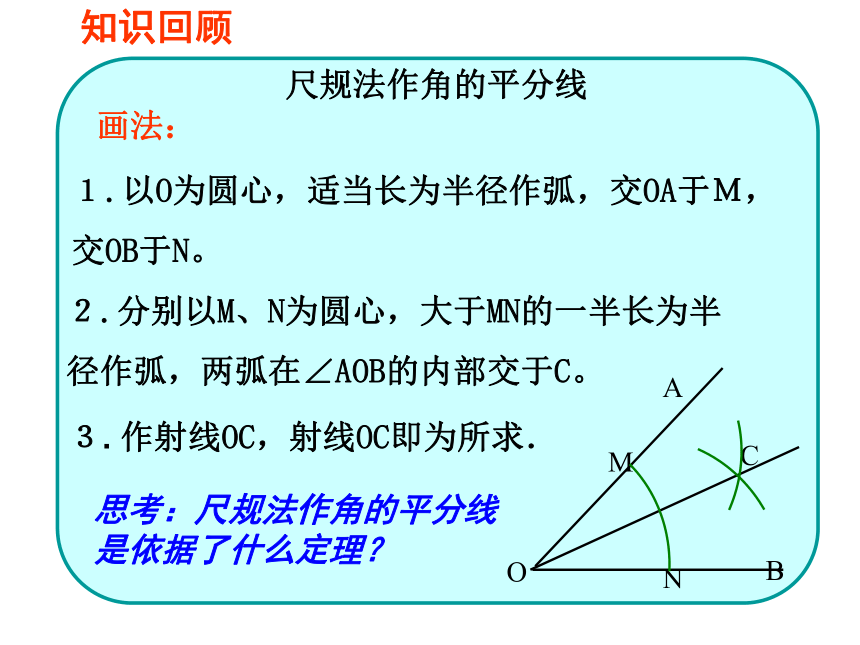
尺规法作角的平分线
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
2.分别以M、N为圆心,大于MN的一半长为半径作弧,两弧在∠AOB的内部交于C。
3. 作射线OC,射线OC即为所求.
O
A
B
N
M
C
知识回顾
思考:尺规法作角的平分线是依据了什么定理?
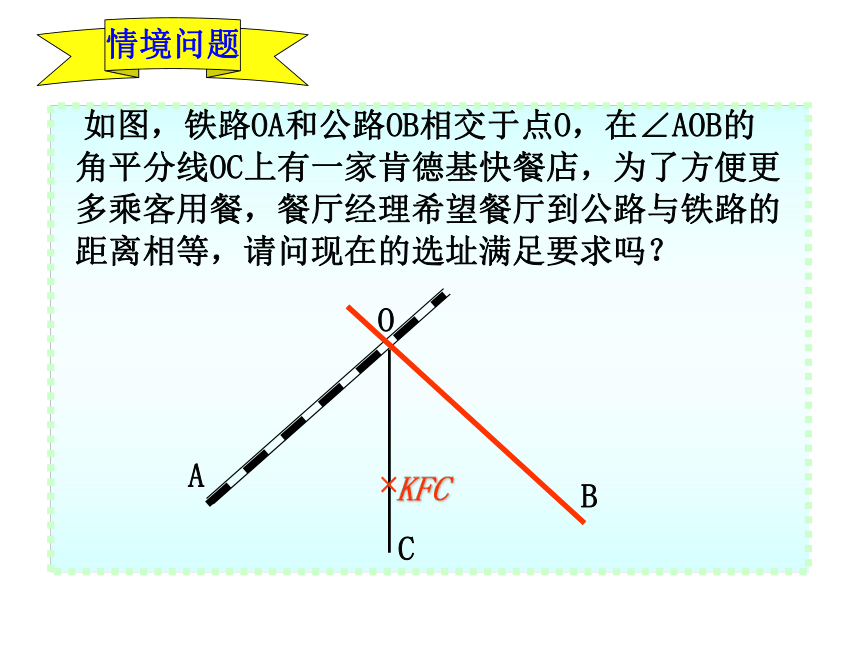
情境问题
如图,铁路OA和公路OB相交于点O,在∠AOB的角平分线OC上有一家肯德基快餐店,为了方便更多乘客用餐,餐厅经理希望餐厅到公路与铁路的距离相等,请问现在的选址满足要求吗?
KFC
O
B
A
×
C
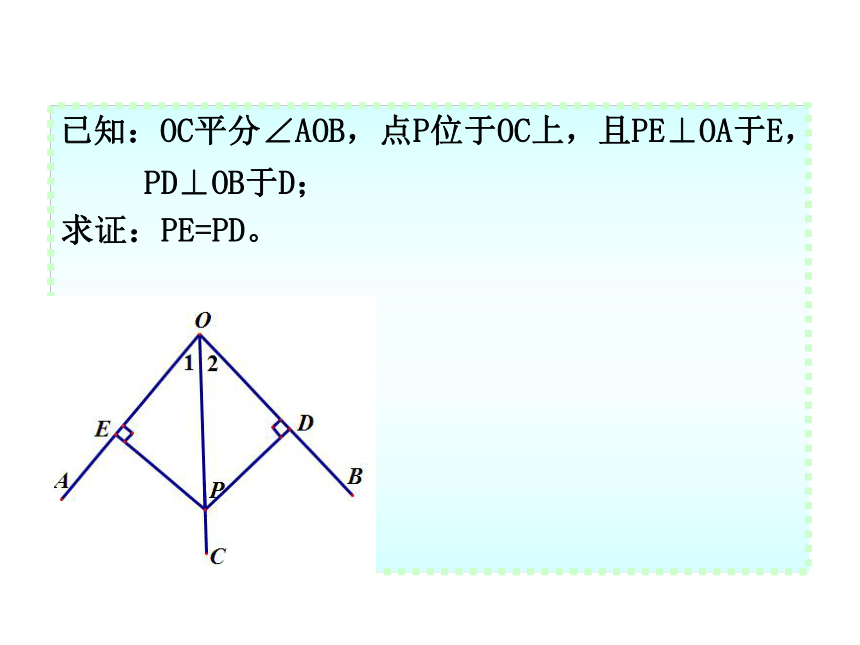
已知:OC平分∠AOB,点P位于OC上,且PE⊥OA于E,
PD⊥OB于D;
求证:PE=PD。
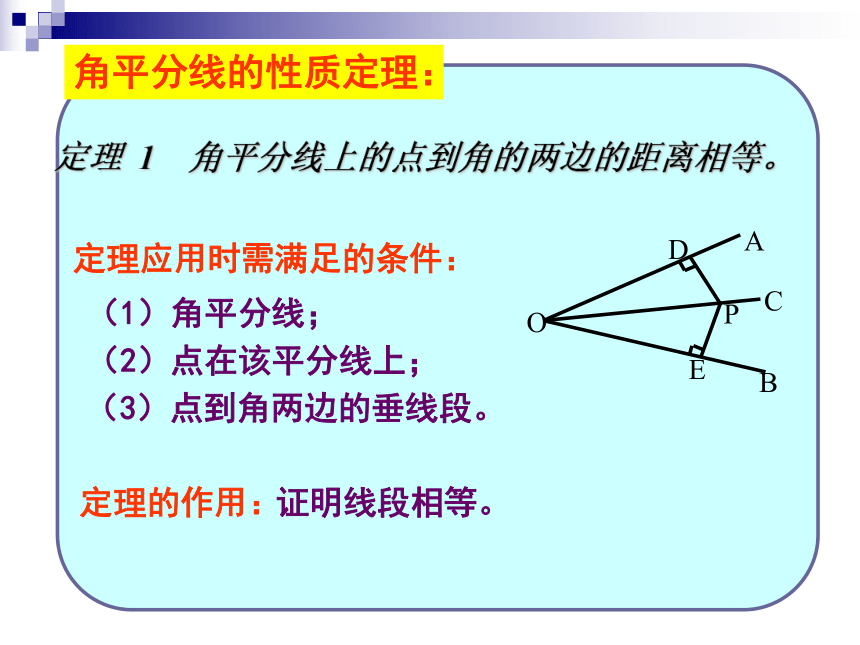
角平分线的性质定理:
定理 1 角平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用时需满足的条件:
(1)角平分线;
(2)点在该平分线上;
(3)点到角两边的垂线段。
定理的作用:
证明线段相等。
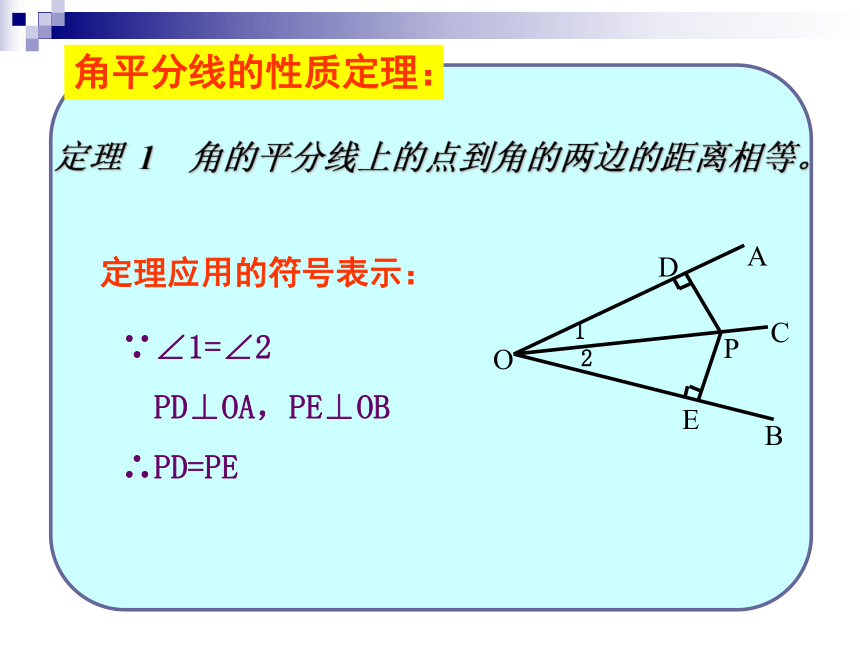
角平分线的性质定理:
定理 1 角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用的符号表示:
∵∠1=∠2
PD⊥OA,PE⊥OB
∴PD=PE
1
2
甲同学说:如果点P在∠AOB的角平分线上,那
么一定有PE=PD。
乙同学说:如果PD⊥OB,PE⊥OA,就一定有
PD=PE。
在∠AOB的内部有一点P,PE交OA边于E,PD交OB边于D;
角平分线的性质定理:
定理 1 角的平分线上的点到角的两边的距离相等。
定理应用的符号表示:
∵点P在∠AOB的角平分线上(∠1=∠2)
PD⊥OA,PE⊥OB
∴PD=PE
B
A
D
O
P
E
C
1
2
例1.在Rt△ABC中,BD是角平分线,DE⊥AB,垂
足为E,已知DC=5cm,求DE的长度。
A
B
C
D
E
知识应用
变式1.已知△ABC中,∠C=900,AD平分∠CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
例2.已知:△ABC的角平分线BM、CN相交于点P; 求证:点P到三边AB、BC、CA的距离相等。
A
B
C
M
N
P
变式2. 如图,△ABC的∠B的外角平分线BD与∠C的外角平分线CE相交于点P;
求证:点P到三边AB,BC,CA所在直线的距离相等。
A
B
C
D
E
P
B
角平分线的性质:
角的平分线上的点到角的两边的距离相等。
注意:
1、应用定理时必须具备的条件;
2、出现角平分线时常添加的辅助线。
尺规法作角的平分线
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
2.分别以M、N为圆心,大于MN的一半长为半径作弧,两弧在∠AOB的内部交于C。
3. 作射线OC,射线OC即为所求.
O
A
B
N
M
C
知识回顾
思考:尺规法作角的平分线是依据了什么定理?
情境问题
如图,铁路OA和公路OB相交于点O,在∠AOB的角平分线OC上有一家肯德基快餐店,为了方便更多乘客用餐,餐厅经理希望餐厅到公路与铁路的距离相等,请问现在的选址满足要求吗?
KFC
O
B
A
×
C
已知:OC平分∠AOB,点P位于OC上,且PE⊥OA于E,
PD⊥OB于D;
求证:PE=PD。
角平分线的性质定理:
定理 1 角平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用时需满足的条件:
(1)角平分线;
(2)点在该平分线上;
(3)点到角两边的垂线段。
定理的作用:
证明线段相等。
角平分线的性质定理:
定理 1 角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用的符号表示:
∵∠1=∠2
PD⊥OA,PE⊥OB
∴PD=PE
1
2
甲同学说:如果点P在∠AOB的角平分线上,那
么一定有PE=PD。
乙同学说:如果PD⊥OB,PE⊥OA,就一定有
PD=PE。
在∠AOB的内部有一点P,PE交OA边于E,PD交OB边于D;
角平分线的性质定理:
定理 1 角的平分线上的点到角的两边的距离相等。
定理应用的符号表示:
∵点P在∠AOB的角平分线上(∠1=∠2)
PD⊥OA,PE⊥OB
∴PD=PE
B
A
D
O
P
E
C
1
2
例1.在Rt△ABC中,BD是角平分线,DE⊥AB,垂
足为E,已知DC=5cm,求DE的长度。
A
B
C
D
E
知识应用
变式1.已知△ABC中,∠C=900,AD平分∠CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
例2.已知:△ABC的角平分线BM、CN相交于点P; 求证:点P到三边AB、BC、CA的距离相等。
A
B
C
M
N
P
变式2. 如图,△ABC的∠B的外角平分线BD与∠C的外角平分线CE相交于点P;
求证:点P到三边AB,BC,CA所在直线的距离相等。
A
B
C
D
E
P
B
角平分线的性质:
角的平分线上的点到角的两边的距离相等。
注意:
1、应用定理时必须具备的条件;
2、出现角平分线时常添加的辅助线。
