必修2第七章第二节功学案
图片预览


文档简介
班级 姓名 学号
高一物理第七章《功》导学案
学习目标 1、 理解功的概念,知道做功的两个因素
2 、明确功是标量,知道W=FLcosθ的适用范围,会用功的公式进行计算
3、 理解正功、负功的概念
重点难点 功的概念(实际情况中如何理解力和力的方向上的位移)
●【课前预习】
1.功的概念:一个物体受到___作用,如果在力的方向上发生一段 ,这个力就对物体做了功。
2.做功的两个不可缺少的因素:___和力的方向上发生的___。
3.功的大小:力对物体做功的大小等于力的大小、位移的大小、力与位移夹角的__ 这三者的乘积,其表达式为 。
4.功的单位:在国际单位制中,功的单位是___,简称___,符号是___。
1J等于___的力使物体在力的方向上发生___的位移时所做的功。
5.功的量性:功是___量。(矢量、标量)
6.正功和负功:根据W=FLcosα可知
(1)当α=___时,W=0,即当力和位移___时,力对物体不做功,这种情况,物体在力的方向上没有发生位移。
(2)当___≤α<___时,W>0。即当力和位移的夹角为___(锐﹑钝)角时,力F为___(动﹑阻)力对物体做___功;
(3)当___<α≤___时,W<0。即当力和位移的夹角为___(锐,钝)角时,力F为___(动,阻)力对物体做___功;又常说成物体___这个力做功(取绝对值)。
●探究过程:
一、功的概念
回顾初中学过的与功的概念密切相关的如下两个问题:什么叫做功?谁对谁做功?
结论:(1)如果一个物体受到力的作用,并且在力的方向上发生了位移,物理学中就说这个力对物体做了功。
(2)物理学中,力和物体在力的方向上发生的位移,是做功的两个不可缺少的因素。
二、功的公式
如图1:力F使滑块发生位移S这个过程中,F对滑块做了多少功如何计算?
如图2所示,这种情况下滑块沿F方向的位移是多少?
功的公式: W=FLcos α
1、力对物体所做的功,等于力的大小、位移的大小、力和位移的夹角的余弦三者的乘积。
2、在国际单位制中,功的单位是焦耳(J) 1J=1N·m
三、正功、负功
1、对功的计算公式W=FLcos α的可能值讨论:(从cos α的可能值入手讨论)指出功W可能为正值、负值或零
(1)当0°≤α<90°时,cos α为正值,W为正值,称为力对物体做正功,称为力对物体做功。
(2)当α=90°时, cos α=0,W=0,力对物体做零功,即力对物体不做功。
(3)当90°<α≤180°时,cos α为负值,W为负值,称为力对物体做负功,或说物体克服这个力做功。
2、讨论功的物理意义,然后再说明正功、负功的物理意义。
①功是描述什么的物理量?(功是力在空间位移上逐渐累积的作用过程。)
②这个累积作用过程到底累积什么?
结论:a、功是描述力在空间位移上累积作用的物理量。功是能量转化的量度,功是标量。
b 、正功和负功的意义:
正功的意义是:力对物体做功向物体提供能量,即受力物体获得了能量。
负功的意义是:物体克服外力做功,向外输出能量(以消耗自身的能量为代价),即负功表示物体失去了能量。
●实例探究:
1、恒力的功,直接利用W=FLcosα来计算
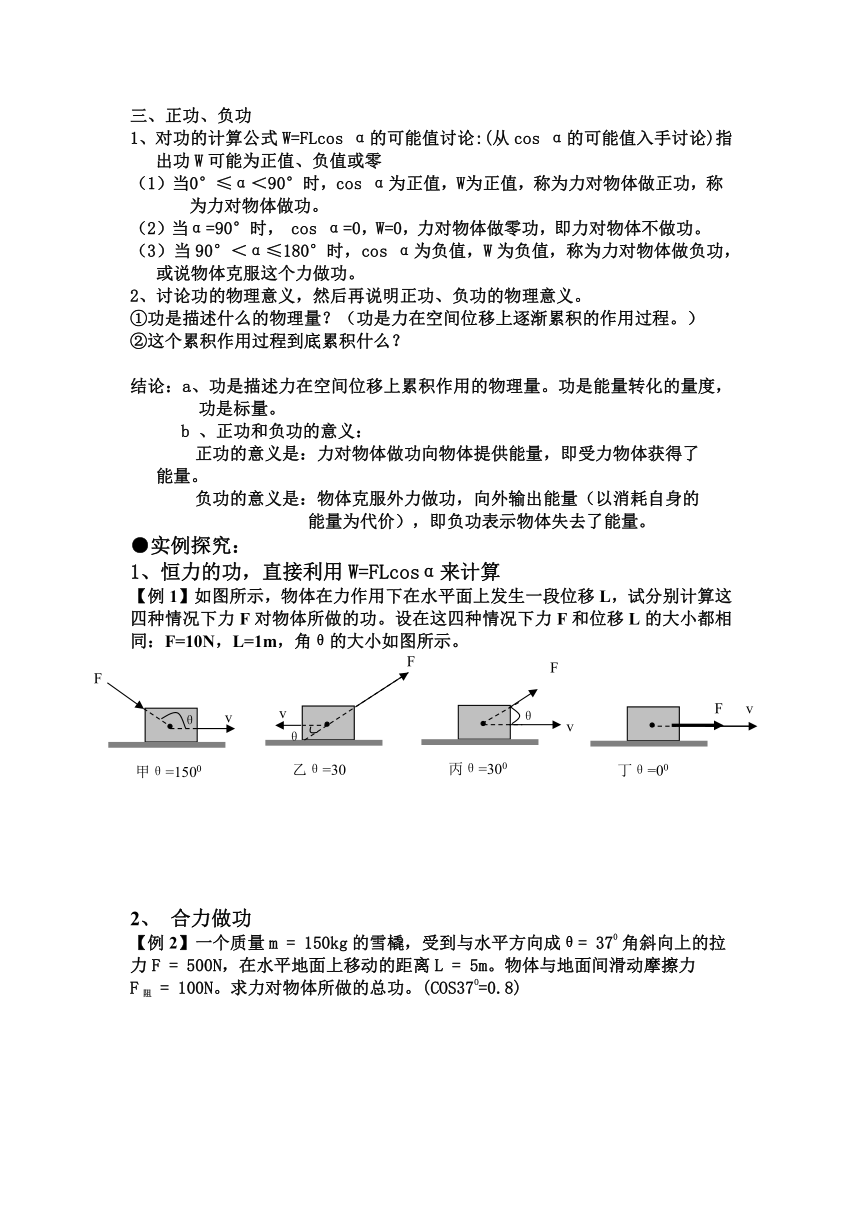
【例1】如图所示,物体在力作用下在水平面上发生一段位移L,试分别计算这四种情况下力F对物体所做的功。设在这四种情况下力F和位移L的大小都相同:F=10N,L=1m,角θ的大小如图所示。
2、 合力做功
【例2】一个质量m = 150kg的雪橇,受到与水平方向成θ= 370 角斜向上的拉
力F = 500N,在水平地面上移动的距离L = 5m。物体与地面间滑动摩擦力
F阻 = 100N。求力对物体所做的总功。(COS37O=0.8)
3、分析摩擦力做功
不论是静摩擦力,还是滑动摩擦力既可以对物体做正功,也可以对物体做负功,还可能不对物体做功。
【例3】关于力对物体做功,如下说法正确的是
A.滑动摩擦力对物体一定做负功 B.静摩擦力对物体可能做正功
C.作用力的功与反作用力的功其代数和一定为零
D.合外力对物体不做功,物体一定处于平衡状态
4、求变力的功
【例4】以一定的初速度竖直向上抛出一小球,小球上升的最大高度为h,空气阻力的大小恒为F.则从抛出到落回到抛出点的过程中,求空气阻力对小球做的功?
5、利用力-位移图象求功.
在F—x图象中图线与两坐标轴所围的“面积” 的代数和表示F做的功。“面积”有正负,在x轴上方的“面积”为正,在x轴下方的“面积” 为负
【例5】如图:求此变力在物体发生20m位移的过程中做的功
【课堂练习】(A层)
1.下列说法中正确的是( )
A.功是矢量,正、负表示方向
B.功是标量,正号表示外力对物体做功,负号表示物体克服外力做功
C.力对物体做正功还是做负功,取决于力和位移的方向关系
D.力做功总是在某过程中完成的,所以功是一个过程量
2、物体在两个相互垂直的力作用下运动,力F1对物体做功6J,物体克服力F2做功8J,则F1、F2的合力对物体做功为( )
A.14J B.10J C.2J D.-2J
3、质量为m的物体,在水平力F作用下,在粗糙的水平面上运动,哪些说法正确
A.如果物体做加速直线运动,F一定对物体做正功
B.如果物体做减速直线运动,F一定对物体做负功
C.如果物体做减速直线运动,F也可能对物体做正功
D.如果物体做匀速直线运动,F一定对物体做正功
4、如图1-1-8所示 ,物体在水平桌面上,当对它施加图A的拉力F,使它由静止发生位移s,与对它施加图B的推力F,使它由静止发生位移s,F与水平方向夹角均为α,则关于做功的下述说法中正确的是( )
A.图B中F做功多
B.A、B中F做功相同
C.图B中克服摩擦力做功多
D.A、B中克服摩擦力做功相同
5.如图2-2-9所示,A、B两物体叠放在一起,用一不可伸长的水平细绳子把A系于左边的墙上,B在拉力F作用下向右匀速运动,在这过程中,A、B间的摩擦力的做功情况是( )
A、对A、B都做负功 B、对A不做功,对B做负功
C、对A做正功,对B做负功 D、对A、B都不做功
6. 如图2-2-11所示,用50 N的力拉一个质量为10kg的物体在水平地面上前进,若物体前进了10m,求(1)拉力F做的功(2)重力G做的功(3)如果物体与水平面间动摩擦因数μ=0.1,物体克服阻力做功(sin370=0.6,cos370=0.8,g=10m/s2)
【课外拓展】(B层)
1、静止在光滑水平面上质量为1kg的物体,受到图2-2-13所示水平变力的作用,则在这2s内力F共对物体做了多少功
2.质量为m的木箱放在倾角为α的斜面上,水平力F作用在木箱上,使它沿斜面匀速向上移动了s,如图1-1-9所示,试分析作用在木箱上有几个力,各力对木箱做功为多少 合力所做的功为多少
3.如图2-2-12所示,物体A的质量为2kg,置于光滑的水平面上,水平拉力2N,不计绳子与滑轮的摩擦和滑轮的质量,物体A获得的加速度a=________m/s2,在物体A移动0.4m的过程中,拉力F做功________J.
4.如图所示,某力F大小等于10 N保持不变,作用在半径R=1 m的转盘的边缘上,方向任何时刻均沿过作用点的切线方向,则在转盘转动一周的过程中,力F所做的功为( )
A.0 J B.10 J
C.20πJ D.无法确定
图
高一物理第七章《功》导学案答案
【例1】W1=FLcos(180o-θ)=10×1×=5J
W2=FLcos(180o-θ)=10×1×(-)=-5J
W3= FLcosθ=10×1×=5J
W4=FL=10×1=10J
【例2】拉力做的功:W1=FLcos37o
阻力做的功:W2= -F阻L
合力做的总功:W= W1+ W2= FLcos37o-F阻L=1500J
【例3】B
【例4】解析:小球从抛出到落回到抛出点的过程中,虽然物体的位移为零,但空气阻力做的功并不为零.因为小球上升和下落过程中空气阻力虽然大小不变,但其方向发生了变化,不是恒力,不能直接用W=FLcosα计算.如果把运动的全过程分成两段,上升过程中空气阻力大小、方向均不变,可求出阻力做的功W1=Fhcos180°=-Fh;下降过程做功W2=Fhcos180°=-Fh,所以全过程中空气阻力做功W=W1+W2=-2Fh.
【例5】解析:此变力在物体发生20m位移的过程中做的功在数值上等于图中阴影线标出的梯形面积。W=(5+20)×20=250J
【课堂练习】(A层)
1、【解析】选B、C、D.功是标量,只有大小,没有方向,故A错,功有正负,正功表示外力对物体做功,负功表示物体克服外力做功,功的正负取决于力和位移的夹角,即力和位移的方向关系,故B、C正确,功总与一段位移相对应,因此是过程量,故D正确.
2、D
3、ACD
4、【解析】选B、C.力F做功WF=F·scosα,两图中F做功相同,A错、B对;由于摩擦力fA=μ(mg-Fsinα),fB=μ(mg+Fsinα),所以克服摩擦力做功WA=fAs=μ(mg-Fsinα)·s,WB=fBs=μ(mg+Fsinα)s,C对、D错.
5、B
6、(1)拉力做的功:WF=FLcos37o=50×10×0.8=400J
(2)重力做的功:WG=0J
(3)对物体受力分析如图:
Ff=μ(mg-Fcos37o)
摩擦力做的功:WFf=-Ffl=-μ(mg-Fcos37o)l=-6J
【课外拓展】
1、答案:0
2、【解析】对木箱受力分析如图所示.受重力mg,支持力N,水平推力F,摩擦力f,共四个力作用.
WN=Nscos90°=0
WF=Fscos α
WG=-mgssinα
Wf=-fs=(mgsinα-Fcosα)s
W总=WN+WF+WG+Wf=0
答案:四个力 WN=0 WF=Fscosα
WG=-mgssinα Wf=(mgsinα-Fcosα)s
W总=0
3.解析:由牛顿第二定律得:2F=ma
a==2m/s2
拉力F做的功:WF=F2L=2×2×0.4=1.6J
4、解析:采用无限分割再求其和的思维方法求特殊情况下变力的功(本题中易犯毛病是认为位移为零,力F做功为零),功是一个过程量,研究功不能只简单地看初、末状态,而应该研究整个过程.
由于力F的方向总与该时刻的速度方向一致,因此做功不为零,为求力F所做的功,可把作用点所在的圆周分成无限多很短的小段如Δs1、Δs2、Δs3……来研究,对每一足够小的小段来说,力F的方向与该小段的位移方向一致,可用公式W=Fs求功,则在力F作用下圆盘转动一周的过程中,力F所做的功为:
W=F·Δs1+F·Δs2+F·Δs3+…=F(Δs1+Δs2+Δs3+…)=F·2πr=10×2π×1J=20πJ.
选项C正确.
答案:C
甲θ=1500
F
v
θ
乙θ=30
F
v
θ
丙θ=300
v
θ
丁θ=00
F v
F
2-2-12
F
A
高一物理第七章《功》导学案
学习目标 1、 理解功的概念,知道做功的两个因素
2 、明确功是标量,知道W=FLcosθ的适用范围,会用功的公式进行计算
3、 理解正功、负功的概念
重点难点 功的概念(实际情况中如何理解力和力的方向上的位移)
●【课前预习】
1.功的概念:一个物体受到___作用,如果在力的方向上发生一段 ,这个力就对物体做了功。
2.做功的两个不可缺少的因素:___和力的方向上发生的___。
3.功的大小:力对物体做功的大小等于力的大小、位移的大小、力与位移夹角的__ 这三者的乘积,其表达式为 。
4.功的单位:在国际单位制中,功的单位是___,简称___,符号是___。
1J等于___的力使物体在力的方向上发生___的位移时所做的功。
5.功的量性:功是___量。(矢量、标量)
6.正功和负功:根据W=FLcosα可知
(1)当α=___时,W=0,即当力和位移___时,力对物体不做功,这种情况,物体在力的方向上没有发生位移。
(2)当___≤α<___时,W>0。即当力和位移的夹角为___(锐﹑钝)角时,力F为___(动﹑阻)力对物体做___功;
(3)当___<α≤___时,W<0。即当力和位移的夹角为___(锐,钝)角时,力F为___(动,阻)力对物体做___功;又常说成物体___这个力做功(取绝对值)。
●探究过程:
一、功的概念
回顾初中学过的与功的概念密切相关的如下两个问题:什么叫做功?谁对谁做功?
结论:(1)如果一个物体受到力的作用,并且在力的方向上发生了位移,物理学中就说这个力对物体做了功。
(2)物理学中,力和物体在力的方向上发生的位移,是做功的两个不可缺少的因素。
二、功的公式
如图1:力F使滑块发生位移S这个过程中,F对滑块做了多少功如何计算?
如图2所示,这种情况下滑块沿F方向的位移是多少?
功的公式: W=FLcos α
1、力对物体所做的功,等于力的大小、位移的大小、力和位移的夹角的余弦三者的乘积。
2、在国际单位制中,功的单位是焦耳(J) 1J=1N·m
三、正功、负功
1、对功的计算公式W=FLcos α的可能值讨论:(从cos α的可能值入手讨论)指出功W可能为正值、负值或零
(1)当0°≤α<90°时,cos α为正值,W为正值,称为力对物体做正功,称为力对物体做功。
(2)当α=90°时, cos α=0,W=0,力对物体做零功,即力对物体不做功。
(3)当90°<α≤180°时,cos α为负值,W为负值,称为力对物体做负功,或说物体克服这个力做功。
2、讨论功的物理意义,然后再说明正功、负功的物理意义。
①功是描述什么的物理量?(功是力在空间位移上逐渐累积的作用过程。)
②这个累积作用过程到底累积什么?
结论:a、功是描述力在空间位移上累积作用的物理量。功是能量转化的量度,功是标量。
b 、正功和负功的意义:
正功的意义是:力对物体做功向物体提供能量,即受力物体获得了能量。
负功的意义是:物体克服外力做功,向外输出能量(以消耗自身的能量为代价),即负功表示物体失去了能量。
●实例探究:
1、恒力的功,直接利用W=FLcosα来计算
【例1】如图所示,物体在力作用下在水平面上发生一段位移L,试分别计算这四种情况下力F对物体所做的功。设在这四种情况下力F和位移L的大小都相同:F=10N,L=1m,角θ的大小如图所示。
2、 合力做功
【例2】一个质量m = 150kg的雪橇,受到与水平方向成θ= 370 角斜向上的拉
力F = 500N,在水平地面上移动的距离L = 5m。物体与地面间滑动摩擦力
F阻 = 100N。求力对物体所做的总功。(COS37O=0.8)
3、分析摩擦力做功
不论是静摩擦力,还是滑动摩擦力既可以对物体做正功,也可以对物体做负功,还可能不对物体做功。
【例3】关于力对物体做功,如下说法正确的是
A.滑动摩擦力对物体一定做负功 B.静摩擦力对物体可能做正功
C.作用力的功与反作用力的功其代数和一定为零
D.合外力对物体不做功,物体一定处于平衡状态
4、求变力的功
【例4】以一定的初速度竖直向上抛出一小球,小球上升的最大高度为h,空气阻力的大小恒为F.则从抛出到落回到抛出点的过程中,求空气阻力对小球做的功?
5、利用力-位移图象求功.
在F—x图象中图线与两坐标轴所围的“面积” 的代数和表示F做的功。“面积”有正负,在x轴上方的“面积”为正,在x轴下方的“面积” 为负
【例5】如图:求此变力在物体发生20m位移的过程中做的功
【课堂练习】(A层)
1.下列说法中正确的是( )
A.功是矢量,正、负表示方向
B.功是标量,正号表示外力对物体做功,负号表示物体克服外力做功
C.力对物体做正功还是做负功,取决于力和位移的方向关系
D.力做功总是在某过程中完成的,所以功是一个过程量
2、物体在两个相互垂直的力作用下运动,力F1对物体做功6J,物体克服力F2做功8J,则F1、F2的合力对物体做功为( )
A.14J B.10J C.2J D.-2J
3、质量为m的物体,在水平力F作用下,在粗糙的水平面上运动,哪些说法正确
A.如果物体做加速直线运动,F一定对物体做正功
B.如果物体做减速直线运动,F一定对物体做负功
C.如果物体做减速直线运动,F也可能对物体做正功
D.如果物体做匀速直线运动,F一定对物体做正功
4、如图1-1-8所示 ,物体在水平桌面上,当对它施加图A的拉力F,使它由静止发生位移s,与对它施加图B的推力F,使它由静止发生位移s,F与水平方向夹角均为α,则关于做功的下述说法中正确的是( )
A.图B中F做功多
B.A、B中F做功相同
C.图B中克服摩擦力做功多
D.A、B中克服摩擦力做功相同
5.如图2-2-9所示,A、B两物体叠放在一起,用一不可伸长的水平细绳子把A系于左边的墙上,B在拉力F作用下向右匀速运动,在这过程中,A、B间的摩擦力的做功情况是( )
A、对A、B都做负功 B、对A不做功,对B做负功
C、对A做正功,对B做负功 D、对A、B都不做功
6. 如图2-2-11所示,用50 N的力拉一个质量为10kg的物体在水平地面上前进,若物体前进了10m,求(1)拉力F做的功(2)重力G做的功(3)如果物体与水平面间动摩擦因数μ=0.1,物体克服阻力做功(sin370=0.6,cos370=0.8,g=10m/s2)
【课外拓展】(B层)
1、静止在光滑水平面上质量为1kg的物体,受到图2-2-13所示水平变力的作用,则在这2s内力F共对物体做了多少功
2.质量为m的木箱放在倾角为α的斜面上,水平力F作用在木箱上,使它沿斜面匀速向上移动了s,如图1-1-9所示,试分析作用在木箱上有几个力,各力对木箱做功为多少 合力所做的功为多少
3.如图2-2-12所示,物体A的质量为2kg,置于光滑的水平面上,水平拉力2N,不计绳子与滑轮的摩擦和滑轮的质量,物体A获得的加速度a=________m/s2,在物体A移动0.4m的过程中,拉力F做功________J.
4.如图所示,某力F大小等于10 N保持不变,作用在半径R=1 m的转盘的边缘上,方向任何时刻均沿过作用点的切线方向,则在转盘转动一周的过程中,力F所做的功为( )
A.0 J B.10 J
C.20πJ D.无法确定
图
高一物理第七章《功》导学案答案
【例1】W1=FLcos(180o-θ)=10×1×=5J
W2=FLcos(180o-θ)=10×1×(-)=-5J
W3= FLcosθ=10×1×=5J
W4=FL=10×1=10J
【例2】拉力做的功:W1=FLcos37o
阻力做的功:W2= -F阻L
合力做的总功:W= W1+ W2= FLcos37o-F阻L=1500J
【例3】B
【例4】解析:小球从抛出到落回到抛出点的过程中,虽然物体的位移为零,但空气阻力做的功并不为零.因为小球上升和下落过程中空气阻力虽然大小不变,但其方向发生了变化,不是恒力,不能直接用W=FLcosα计算.如果把运动的全过程分成两段,上升过程中空气阻力大小、方向均不变,可求出阻力做的功W1=Fhcos180°=-Fh;下降过程做功W2=Fhcos180°=-Fh,所以全过程中空气阻力做功W=W1+W2=-2Fh.
【例5】解析:此变力在物体发生20m位移的过程中做的功在数值上等于图中阴影线标出的梯形面积。W=(5+20)×20=250J
【课堂练习】(A层)
1、【解析】选B、C、D.功是标量,只有大小,没有方向,故A错,功有正负,正功表示外力对物体做功,负功表示物体克服外力做功,功的正负取决于力和位移的夹角,即力和位移的方向关系,故B、C正确,功总与一段位移相对应,因此是过程量,故D正确.
2、D
3、ACD
4、【解析】选B、C.力F做功WF=F·scosα,两图中F做功相同,A错、B对;由于摩擦力fA=μ(mg-Fsinα),fB=μ(mg+Fsinα),所以克服摩擦力做功WA=fAs=μ(mg-Fsinα)·s,WB=fBs=μ(mg+Fsinα)s,C对、D错.
5、B
6、(1)拉力做的功:WF=FLcos37o=50×10×0.8=400J
(2)重力做的功:WG=0J
(3)对物体受力分析如图:
Ff=μ(mg-Fcos37o)
摩擦力做的功:WFf=-Ffl=-μ(mg-Fcos37o)l=-6J
【课外拓展】
1、答案:0
2、【解析】对木箱受力分析如图所示.受重力mg,支持力N,水平推力F,摩擦力f,共四个力作用.
WN=Nscos90°=0
WF=Fscos α
WG=-mgssinα
Wf=-fs=(mgsinα-Fcosα)s
W总=WN+WF+WG+Wf=0
答案:四个力 WN=0 WF=Fscosα
WG=-mgssinα Wf=(mgsinα-Fcosα)s
W总=0
3.解析:由牛顿第二定律得:2F=ma
a==2m/s2
拉力F做的功:WF=F2L=2×2×0.4=1.6J
4、解析:采用无限分割再求其和的思维方法求特殊情况下变力的功(本题中易犯毛病是认为位移为零,力F做功为零),功是一个过程量,研究功不能只简单地看初、末状态,而应该研究整个过程.
由于力F的方向总与该时刻的速度方向一致,因此做功不为零,为求力F所做的功,可把作用点所在的圆周分成无限多很短的小段如Δs1、Δs2、Δs3……来研究,对每一足够小的小段来说,力F的方向与该小段的位移方向一致,可用公式W=Fs求功,则在力F作用下圆盘转动一周的过程中,力F所做的功为:
W=F·Δs1+F·Δs2+F·Δs3+…=F(Δs1+Δs2+Δs3+…)=F·2πr=10×2π×1J=20πJ.
选项C正确.
答案:C
甲θ=1500
F
v
θ
乙θ=30
F
v
θ
丙θ=300
v
θ
丁θ=00
F v
F
2-2-12
F
A
