人教版八年级上册数学:12.2三角形全等的判定 讲义(学案)
文档属性
| 名称 | 人教版八年级上册数学:12.2三角形全等的判定 讲义(学案) |  | |
| 格式 | doc | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-08 15:02:09 | ||
图片预览


文档简介
第五讲 三角形全等的判定 (SSS)
第一部分 知识清单
全等三角形的判定方法(一) 掌握
第二部分 例题研究
知识引入:
探究一:讨论三角形全等的条件(动手画一画并回答下列问题)
(1)只给一个条件:一组对应边相等(或一组对应角相等),画出的两个三角形一定全等吗?
(2)给出两个条件画三角形,有____种情形。按下面给出的两个条件,画出的两个三角形一定全等吗?
(3)给出三个条件画三角形,有____种情形。按下面给出三个条件,画出的两个三角形一定全等吗?
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
a.作图方法:画全等三角形(尺规作图 用直尺(没有刻度)与圆规进行作图)
b.把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的.
c.归纳:三边对应相等的两个三角形 ,简写为“ ”或“ ”.
d、用数学语言表述:
(4)归纳;由上面的画图和实验可以得出全等三角形判定(一):
三边分别对应相等的两个三角形 (可以简写成“ ”或“ ”)
知识点一:全等三角形的判定方法(一) 边边边(SSS)
三边分别对应相等的两个三角形全等,可以简写成“边边边或“SSS”)
用数学语言表述:
例1 如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
证明:∵D是BC
∴ =
∴在△ 和△ 中有:
AB=
BD=
AD=
∴△ABD △ACD( )
例2 如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ ADE。
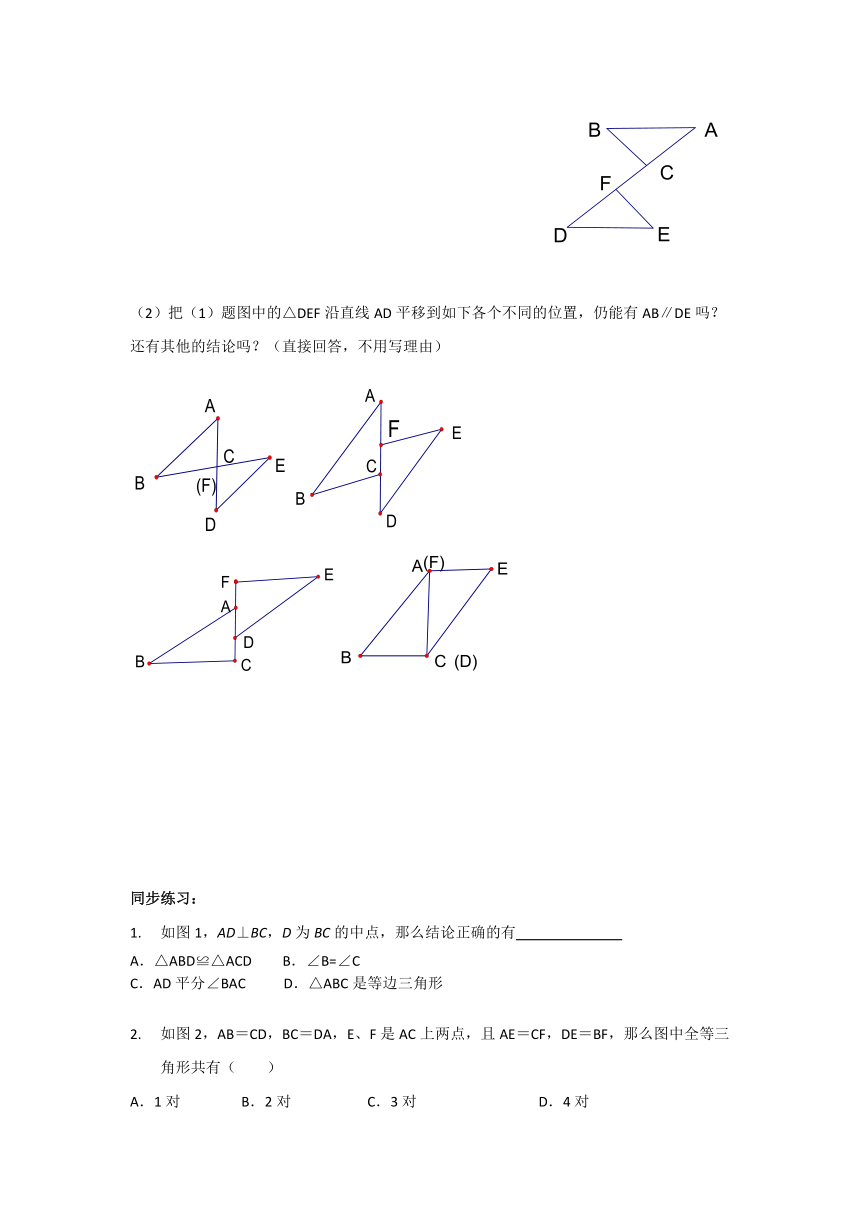
例3 (1) 如图,点ACFD在同一条直线上,AF=DC,AB=DE,BC=EF。求证:AB∥DE
(2)把(1)题图中的△DEF沿直线AD平移到如下各个不同的位置,仍能有AB∥DE吗?还有其他的结论吗?(直接回答,不用写理由)
同步练习:
如图1,AD⊥BC,D为BC的中点,那么结论正确的有
A.△ABD≌△ACD B.∠B=∠C
C.AD平分∠BAC D.△ABC是等边三角形
如图2,AB=CD,BC=DA,E、F是AC上两点,且AE=CF,DE=BF,那么图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
如图3,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是________.
图1 图2 图3
如下图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。
解:∵BE=CF (_____________)
∴BE+EC=CF+EC
即BC=EF
在ΔABC和ΔDEF中
AB=________ (________________)
__________=DF(_______________)
BC=__________
∴ΔABC≌ΔDEF (_____________)
已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC。
如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
课后作业:
1. 已知:如图,AB=CD,AD=CB,求证:△ABC≌△CDA.
2. 已知:如图,AB=DC,AC=DB.求证:(1)∠ACB=∠DBC;(2).
3. 已知:如图,AB=AC,D是BC中点,
(1) 求证:△ABD≌△ACD;(2) 求证:AD⊥BC;
(3) 若∠BAD=25°,则∠BAC是多少度?
4. 已知:如图,四边形ABCD中,AB=AD,BC=DC.求证:∠B=∠D.
第一部分 知识清单
全等三角形的判定方法(一) 掌握
第二部分 例题研究
知识引入:
探究一:讨论三角形全等的条件(动手画一画并回答下列问题)
(1)只给一个条件:一组对应边相等(或一组对应角相等),画出的两个三角形一定全等吗?
(2)给出两个条件画三角形,有____种情形。按下面给出的两个条件,画出的两个三角形一定全等吗?
(3)给出三个条件画三角形,有____种情形。按下面给出三个条件,画出的两个三角形一定全等吗?
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
a.作图方法:画全等三角形(尺规作图 用直尺(没有刻度)与圆规进行作图)
b.把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的.
c.归纳:三边对应相等的两个三角形 ,简写为“ ”或“ ”.
d、用数学语言表述:
(4)归纳;由上面的画图和实验可以得出全等三角形判定(一):
三边分别对应相等的两个三角形 (可以简写成“ ”或“ ”)
知识点一:全等三角形的判定方法(一) 边边边(SSS)
三边分别对应相等的两个三角形全等,可以简写成“边边边或“SSS”)
用数学语言表述:
例1 如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
证明:∵D是BC
∴ =
∴在△ 和△ 中有:
AB=
BD=
AD=
∴△ABD △ACD( )
例2 如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ ADE。
例3 (1) 如图,点ACFD在同一条直线上,AF=DC,AB=DE,BC=EF。求证:AB∥DE
(2)把(1)题图中的△DEF沿直线AD平移到如下各个不同的位置,仍能有AB∥DE吗?还有其他的结论吗?(直接回答,不用写理由)
同步练习:
如图1,AD⊥BC,D为BC的中点,那么结论正确的有
A.△ABD≌△ACD B.∠B=∠C
C.AD平分∠BAC D.△ABC是等边三角形
如图2,AB=CD,BC=DA,E、F是AC上两点,且AE=CF,DE=BF,那么图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
如图3,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是________.
图1 图2 图3
如下图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。
解:∵BE=CF (_____________)
∴BE+EC=CF+EC
即BC=EF
在ΔABC和ΔDEF中
AB=________ (________________)
__________=DF(_______________)
BC=__________
∴ΔABC≌ΔDEF (_____________)
已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC。
如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
课后作业:
1. 已知:如图,AB=CD,AD=CB,求证:△ABC≌△CDA.
2. 已知:如图,AB=DC,AC=DB.求证:(1)∠ACB=∠DBC;(2).
3. 已知:如图,AB=AC,D是BC中点,
(1) 求证:△ABD≌△ACD;(2) 求证:AD⊥BC;
(3) 若∠BAD=25°,则∠BAC是多少度?
4. 已知:如图,四边形ABCD中,AB=AD,BC=DC.求证:∠B=∠D.
