人教版八年级上册数学12.2三角形全等的判定教案
文档属性
| 名称 | 人教版八年级上册数学12.2三角形全等的判定教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 33.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 00:00:00 | ||
图片预览

文档简介
三角形全等的判定(第一课时)教学设计
学习内容分析
学习目标描述
使学生掌握边边边判定两个三角形全等的方法,会运用这种方法解决问题。
通过有关的证明及应用,教给学生一些基本的数学思想方法,使学生逐步学会分别从题设或结论出发,寻找论证思路,学会用综合法证明问题,从而提高学生分析问题、解决问题的能力。
通过学生探究特殊角度、特殊边长的三角形全等的条件,再由教师利用课件演示数学事实,让学生充分参与到数学学习的过程中来,获得解决问题的经验;通过习题变式,从中体会事物之间的相互联系与区别,从而进一步培养学生的辩证唯物主义观点。
探究本课的两个判定方法,使学生经历“实践——观察——猜想——验证——归纳——概括”的认知过程,培养学生良好的个性思维品质。
学习内容分析
提示:可从学习内容概述、知识点划分及其相互间的关系等角度分析
本课内容选自人教版《义务教育课程标准实验教科书·数学》八年级上册“12.2三角形全等的判定”(第一课时)
全等三角形是研究图形的重要工具,只有掌握全等三角形的有关内容,并且能灵活的加以运用,才能学好等腰三角形、四边形和圆等内容,同时为今后研究轴对称、旋转等全等变换打下良好的基础。此外,也由于它在日常生活中有着广泛的应用,研究全等三角形,具有重要的意义。
发展学生的合情推理和初步的演绎推理能力是《数学课程标准》的重要要求之一。本章是在七年级下册第七章出现证明和证明格式的基础上,进一步介绍了推理论证的方法。通过定理内容的规范化书写,并在例习题中注重分析思路,让学生学会思考、学会清楚地表达思考的过程,可以进一步培养学生的推理能力。同时,“11.2三角形全等的判定”中几种判定方法,是作为基本事实提出来的,通过画图和实验,让学生确信其正确性,符合学生的认知水平。这样的分析问题、解决问题的方法,对全章乃至以后的学习都是至关重要的。
本节课是全等三角形判定的第一课时,主要探究利用“边边边”方法判定三角形全等,以及简单应用。探索三角形全等的条件,不仅是“全等三角形”知识体系的重要组成部分,而且在探索过程中所体现的思想方法,为学生主动获取知识、感悟三角形全等的数学本质、积累数学活动经验、体验运用类比的方法研究问题等,提供了很好的素材.。通过本节课的学习,可以加深学生对已学几何图形的认识,并为今后的学习奠定基础。
教学目标
1、学生通过动手操作、自主探索、交流,获得新知,增强了动手能力,同时也渗透了分类思想.
在课堂教学中运用实践操作法,让学生进行小组合作学习,在“做”的过程中潜移默化地渗透分类讨论的数学思想方法。
2、明确判定三角形全等需要三个条件。
3、学生通过动手操作、自主探索、交流,获得新知,增强了动手能力,明确判定三角形全等需要三个条件.培养学生合作交流的意识。
4、体验数学在生活中应用的广泛性;检测学生对知识的掌握情况及应用能力,初步体验成功的喜悦;规范证明题的书写过程。
5、通过学习已知角的画法,拓展“边边边”公理
的应用。
教学重点
掌握两个三角形
“边边边”全等判定的条件。
教学难点
探索三角形全等的条件。利用边边边判定两个三角形全等方法的应用及规范化书写。“分类讨论”的数学方法的初步渗透和逻辑思维能力的培养也是本节的难点。
学生学情分析
八年级的学生大约在13岁左右,有一定的学习经验和生活经验,能够根据具体的情境体会三角形全等的判定方法,这些是学习本节课的知识基础。基于学生的学习基础,在研究几何图形的方法和合情推理方面还存在欠缺。本节课是学生在已经掌握了全等三角形的性质后,探索三角形全等的条件。他们经历一些探究的过程:动手实践、观察猜想、归纳总结、巩固应用等。因此,本节课的学习,可以引导学生通过探究研究方法。另外,由于本节课所探究的一种方法,其图形容易辨别,那么,学生如何分析图形之间的内在联系,如何清晰地表达数学思考的过程,也是教师应要特别关注的问题。
教学环节
(一)情境引入
1.多媒体展示,带领学生复习全等三角形的定义及其性质。
学生回答问题:能够完全重合的两个三角形是全等三角形。全等三角形三条边对应相等,三个角分别对应相等.
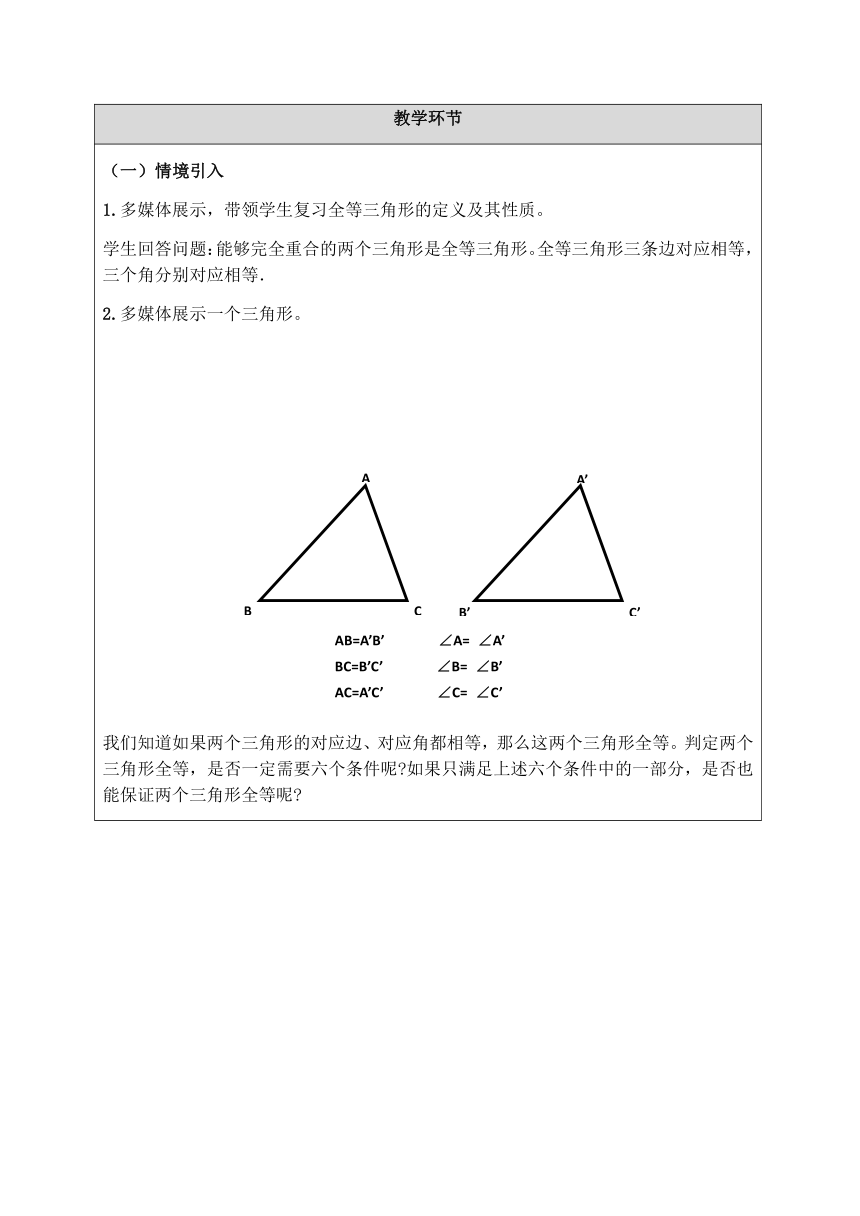
2.多媒体展示一个三角形。
(
A
C
B
A’
C’
B’
AB=A’B’
∠
A=
∠
A’
BC=B’C’
∠
B=
∠
B’
AC=A’C’
∠
C=
∠
C’
)
我们知道如果两个三角形的对应边、对应角都相等,那么这两个三角形全等。判定两个三角形全等,是否一定需要六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?
(二)探究新知
1.多媒体展示:
(1)只给一个条件(一组对应边相等或一组对应角相等),画出的两个三角形一定全等吗?
(2)给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?分别按下列条件做一做.
①三角形一内角为30°,一条边为3cm.
②三角形两内角分别为30°和50°.
③三角形两条边分别为4cm、6cm.
2.学生说出给定三个条件画三角形的各种可能情况.
出示探究2:满足三个条件中的三边对应相等的两个三角形一定全等吗?
3.已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形,并与同伴比较是否全等
4.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
5.如图,已知∠AOB,求作:
,
使
=∠AOB.
(三)课堂训练
1.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
2.如图,
AB=ED,BC=DF,AF=CE.
求证:AB∥DE.
(四)小结归纳
1.三角形全等的判定至少需要三个条件;
2.三角形全等判定的第一个公理是:“边边边”;
3.能用尺规作图法作一个角等于已知角;
4.证明三角形全等的书写格式可分为三部分:第一部分是全等条件的证明;第二部分是罗列两个三角形全等的条件;第三部分是作三角形全等的结论,这里要求注明判定方法。
(五)作业设计
1.教材习题12.2第1题;
2.补充作业:
(1)如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定(
)
A.△ABD≌△ACD
B.△BDE≌△CDE
C.△ABE≌△ACE
D.以上都不对
(2)已知:如图,AC=BD,AD=BC,求证:∠D=∠C.
(3)如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE≌△CBF②∠A=∠C
(六)板书设计
课题
12.2
三角形全等的判定——“边边边”
一、“边边边”公理:
例题分析
尺规作图
二、证明三角形全等的书写格式:
三、尺规作图,作一个角等于已知角的依据:
学习内容分析
学习目标描述
使学生掌握边边边判定两个三角形全等的方法,会运用这种方法解决问题。
通过有关的证明及应用,教给学生一些基本的数学思想方法,使学生逐步学会分别从题设或结论出发,寻找论证思路,学会用综合法证明问题,从而提高学生分析问题、解决问题的能力。
通过学生探究特殊角度、特殊边长的三角形全等的条件,再由教师利用课件演示数学事实,让学生充分参与到数学学习的过程中来,获得解决问题的经验;通过习题变式,从中体会事物之间的相互联系与区别,从而进一步培养学生的辩证唯物主义观点。
探究本课的两个判定方法,使学生经历“实践——观察——猜想——验证——归纳——概括”的认知过程,培养学生良好的个性思维品质。
学习内容分析
提示:可从学习内容概述、知识点划分及其相互间的关系等角度分析
本课内容选自人教版《义务教育课程标准实验教科书·数学》八年级上册“12.2三角形全等的判定”(第一课时)
全等三角形是研究图形的重要工具,只有掌握全等三角形的有关内容,并且能灵活的加以运用,才能学好等腰三角形、四边形和圆等内容,同时为今后研究轴对称、旋转等全等变换打下良好的基础。此外,也由于它在日常生活中有着广泛的应用,研究全等三角形,具有重要的意义。
发展学生的合情推理和初步的演绎推理能力是《数学课程标准》的重要要求之一。本章是在七年级下册第七章出现证明和证明格式的基础上,进一步介绍了推理论证的方法。通过定理内容的规范化书写,并在例习题中注重分析思路,让学生学会思考、学会清楚地表达思考的过程,可以进一步培养学生的推理能力。同时,“11.2三角形全等的判定”中几种判定方法,是作为基本事实提出来的,通过画图和实验,让学生确信其正确性,符合学生的认知水平。这样的分析问题、解决问题的方法,对全章乃至以后的学习都是至关重要的。
本节课是全等三角形判定的第一课时,主要探究利用“边边边”方法判定三角形全等,以及简单应用。探索三角形全等的条件,不仅是“全等三角形”知识体系的重要组成部分,而且在探索过程中所体现的思想方法,为学生主动获取知识、感悟三角形全等的数学本质、积累数学活动经验、体验运用类比的方法研究问题等,提供了很好的素材.。通过本节课的学习,可以加深学生对已学几何图形的认识,并为今后的学习奠定基础。
教学目标
1、学生通过动手操作、自主探索、交流,获得新知,增强了动手能力,同时也渗透了分类思想.
在课堂教学中运用实践操作法,让学生进行小组合作学习,在“做”的过程中潜移默化地渗透分类讨论的数学思想方法。
2、明确判定三角形全等需要三个条件。
3、学生通过动手操作、自主探索、交流,获得新知,增强了动手能力,明确判定三角形全等需要三个条件.培养学生合作交流的意识。
4、体验数学在生活中应用的广泛性;检测学生对知识的掌握情况及应用能力,初步体验成功的喜悦;规范证明题的书写过程。
5、通过学习已知角的画法,拓展“边边边”公理
的应用。
教学重点
掌握两个三角形
“边边边”全等判定的条件。
教学难点
探索三角形全等的条件。利用边边边判定两个三角形全等方法的应用及规范化书写。“分类讨论”的数学方法的初步渗透和逻辑思维能力的培养也是本节的难点。
学生学情分析
八年级的学生大约在13岁左右,有一定的学习经验和生活经验,能够根据具体的情境体会三角形全等的判定方法,这些是学习本节课的知识基础。基于学生的学习基础,在研究几何图形的方法和合情推理方面还存在欠缺。本节课是学生在已经掌握了全等三角形的性质后,探索三角形全等的条件。他们经历一些探究的过程:动手实践、观察猜想、归纳总结、巩固应用等。因此,本节课的学习,可以引导学生通过探究研究方法。另外,由于本节课所探究的一种方法,其图形容易辨别,那么,学生如何分析图形之间的内在联系,如何清晰地表达数学思考的过程,也是教师应要特别关注的问题。
教学环节
(一)情境引入
1.多媒体展示,带领学生复习全等三角形的定义及其性质。
学生回答问题:能够完全重合的两个三角形是全等三角形。全等三角形三条边对应相等,三个角分别对应相等.
2.多媒体展示一个三角形。
(
A
C
B
A’
C’
B’
AB=A’B’
∠
A=
∠
A’
BC=B’C’
∠
B=
∠
B’
AC=A’C’
∠
C=
∠
C’
)
我们知道如果两个三角形的对应边、对应角都相等,那么这两个三角形全等。判定两个三角形全等,是否一定需要六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?
(二)探究新知
1.多媒体展示:
(1)只给一个条件(一组对应边相等或一组对应角相等),画出的两个三角形一定全等吗?
(2)给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?分别按下列条件做一做.
①三角形一内角为30°,一条边为3cm.
②三角形两内角分别为30°和50°.
③三角形两条边分别为4cm、6cm.
2.学生说出给定三个条件画三角形的各种可能情况.
出示探究2:满足三个条件中的三边对应相等的两个三角形一定全等吗?
3.已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形,并与同伴比较是否全等
4.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
5.如图,已知∠AOB,求作:
,
使
=∠AOB.
(三)课堂训练
1.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
2.如图,
AB=ED,BC=DF,AF=CE.
求证:AB∥DE.
(四)小结归纳
1.三角形全等的判定至少需要三个条件;
2.三角形全等判定的第一个公理是:“边边边”;
3.能用尺规作图法作一个角等于已知角;
4.证明三角形全等的书写格式可分为三部分:第一部分是全等条件的证明;第二部分是罗列两个三角形全等的条件;第三部分是作三角形全等的结论,这里要求注明判定方法。
(五)作业设计
1.教材习题12.2第1题;
2.补充作业:
(1)如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定(
)
A.△ABD≌△ACD
B.△BDE≌△CDE
C.△ABE≌△ACE
D.以上都不对
(2)已知:如图,AC=BD,AD=BC,求证:∠D=∠C.
(3)如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE≌△CBF②∠A=∠C
(六)板书设计
课题
12.2
三角形全等的判定——“边边边”
一、“边边边”公理:
例题分析
尺规作图
二、证明三角形全等的书写格式:
三、尺规作图,作一个角等于已知角的依据:
