鲁教版七年级数学上册第一章 三角形综合测评(word 版 含答案)
文档属性
| 名称 | 鲁教版七年级数学上册第一章 三角形综合测评(word 版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 00:00:00 | ||
图片预览


文档简介
第一章 三角形综合测评
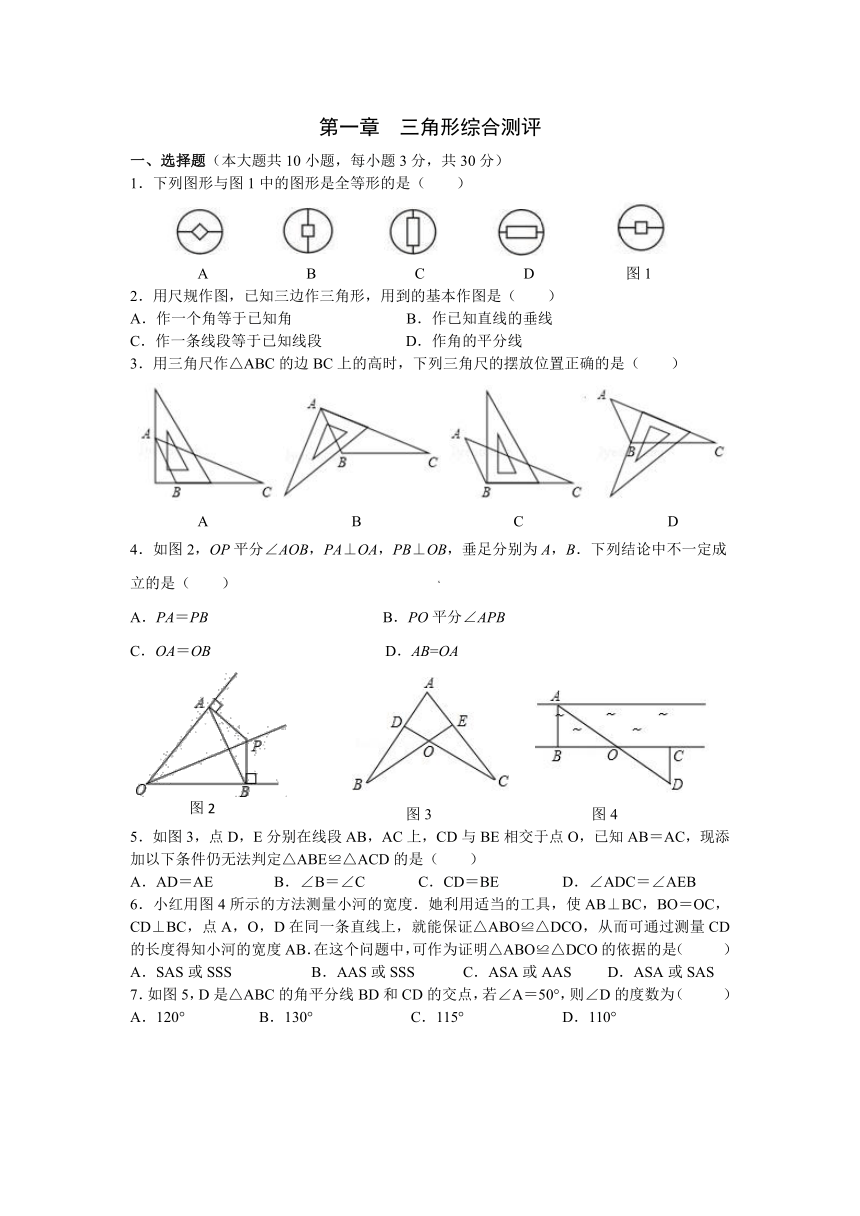
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列图形与图1中的图形是全等形的是( )
A B C D 图1
2.用尺规作图,已知三边作三角形,用到的基本作图是( )
A.作一个角等于已知角 B.作已知直线的垂线
C.作一条线段等于已知线段 D.作角的平分线
3.用三角尺作△ABC的边BC上的高时,下列三角尺的摆放位置正确的是( )
A B C D
4.如图2,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( ) x
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB=OA
图2
图3 图4
5.如图3,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
6.小红用图4所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,BO=OC,CD⊥BC,点A,O,D在同一条直线上,就能保证△ABO≌△DCO,从而可通过测量CD的长度得知小河的宽度AB.在这个问题中,可作为证明△ABO≌△DCO的依据的是( )
A.SAS或SSS B.AAS或SSS C.ASA或AAS D.ASA或SAS
7.如图5,D是△ABC的角平分线BD和CD的交点,若∠A=50°,则∠D的度数为( )
A.120° B.130° C.115° D.110°
图5 图6
8.图6中的a,b,c分别为三角形的三边长,则甲、乙、丙三个三角形和左侧△ABC一定全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
9.如图7,在正方形网格内(每个小正方形的边长为1),有一格点三角形ABC(三个顶点分别在正方形网格的格点上),现需要在网格内构造一个新的格点三角形与原三角形全等,且有一条边与原三角形的一条边重合,这样的三角形可以构造出( )
A.3个 B.4个 C.5个 D.6个
图7 图8
10.如图8,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BDC=180°;③AD=EC;④AC=2CD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题3分,共18分)
11.赵师傅在做完门框后,为防止变形,如图9中所示的那样在门上钉上两条斜拉的木条(即
图中的AB,CD两根木条),其中的数学原理是 .
图9 图10 图11
12.如图10,△ACF≌△DBE,若AD=11,BC=3,则线段AB的长为 .
13.已知∠α和线段a,用尺规作△ABC,使∠A=2∠α,AB=2a,∠B=3∠α,作法如下:①在AN上截取AB=2a,②作∠MAN=2∠α,③以B为圆心,BA为一边作∠ABE=3∠α,BE交AM于点C,△ABC就是所求作的三角形.以上正确的作图顺序是 .(填序号)
14.把长度为9的铁丝截成三段,围成三条边互不相等的三角形,且三边长均为整数,那么这三边长分别为 .
15.如图11,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4 cm2,则阴影部分的面积为 cm2.
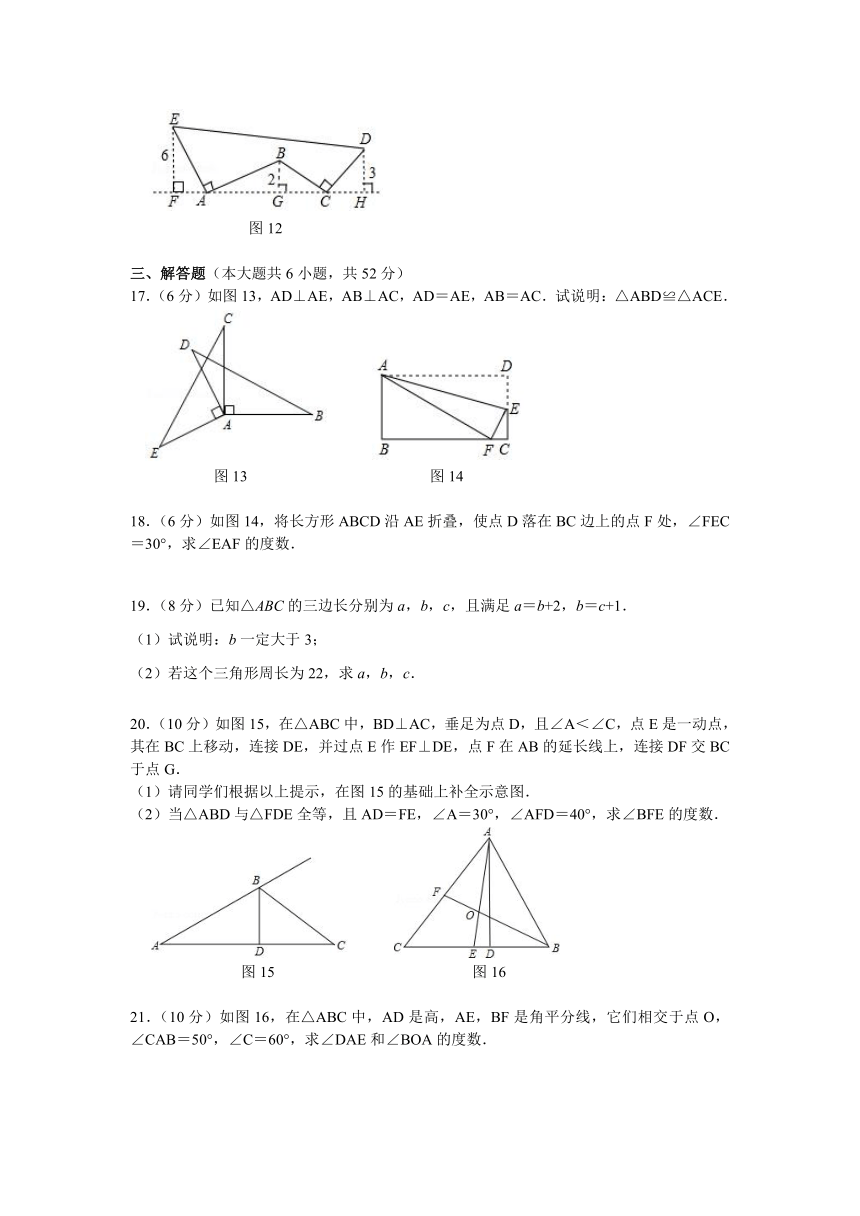
16.如图12,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么按照图中所标注的数据,图中实线所围成的图形面积为 .
图12
三、解答题(本大题共6小题,共52分)
17.(6分)如图13,AD⊥AE,AB⊥AC,AD=AE,AB=AC.试说明:△ABD≌△ACE.
图13 图14
18.(6分)如图14,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,∠FEC=30°,求∠EAF的度数.
19.(8分)已知△ABC的三边长分别为a,b,c,且满足a=b+2,b=c+1.
(1)试说明:b一定大于3;
(2)若这个三角形周长为22,求a,b,c.
20.(10分)如图15,在△ABC中,BD⊥AC,垂足为点D,且∠A<∠C,点E是一动点,其在BC上移动,连接DE,并过点E作EF⊥DE,点F在AB的延长线上,连接DF交BC于点G.
(1)请同学们根据以上提示,在图15的基础上补全示意图.
(2)当△ABD与△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠BFE的度数.
图15 图16
21.(10分)如图16,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.
22.(12分)【问题背景】
如图17,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,试探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先说明△ABE≌△ADG,再说明△AEF≌△AGF,可得出结论,他的结论应是 ,试说明理由;
【探索延伸】
如图18,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=false∠BAD,上述结论是否仍然成立,并说明理由.
附加题(20分,不计入总分)
23.如图19,河边有一条笔直的公路false,公路另一侧是平坦的草地,在数学活动课上,老师要求测量河对岸点B到公路的距离,请你设计一个测量方案.
(1)写出你所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤,并用字母表示测得的数据,求出点B到公路的距离;
(3)试说明你测量的正确性.
图19
第一章 三角形综合测评参考答案
一、1.B 2.C 3.A 4.D 5.C 6.C 7.C 8.B 9.C 10.C
二、11.三角形的稳定性 12.4 13.②①③ 14.2,3,4 15.1 16.40.5
三、17.解:因为AD⊥AE,AB⊥AC,所以∠CAB=∠DAE=90°,所以∠CAB+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.在△ABD和△ACE中,因为AB=AC,∠BAD=∠CAE,AD=AE,所以△ABD≌△ACE.
18.解:因为四边形ABCD是长方形,所以∠D=90°. 依题意,得△ADE≌△AFE,所以∠EFA=∠D=90°,∠AEF=∠AED. 因为∠AEF+∠AED+∠FEC=180°,所以∠AEF=false(180°-∠FEC)=false(180°-30°)=75°,所以∠EAF=90°-∠AEF=90°-75°=15°.
19.解:(1)因为a=b+2,b=c+1,所以b=a-2,b=c+1,所以a-2=c+1,a-c=3.根据三角形的任意两边之差小于第三边,可得a-c<b,所以b一定大于3.
(2)因为b=c+1,所以c=b-1,所以b+2+b+b-1=22,解得b=7,所以a=b+2=9,c=b-1=6.
20.解:(1)补全示意图如图1所示;
图1
(2)因为DE⊥EF,BD⊥AC,所以∠DEF=∠ADB=90°.因为△ABD与△FDE全等,且AD=FE,所以∠ABD=∠FDE.在Rt△ABD中,∠ABD=90°-∠A=60°,所以∠FDE=60°.在Rt△FED中,∠DFE=90°-∠FDE=90°-60°=30°.所以∠BFE=∠BFD+∠DFE=40°+30°=70°.
21.解:因为∠CAB=50°,∠C=60°,所以∠ABC=180°-50°-60°=70°.因为AD是高,所以∠ADC=90°,所以∠DAC=90°-∠C=30°.因为AE,BF是角平分线,所以∠CBF=∠ABF=35°,∠EAC=∠EAB=25°,所以∠DAE=∠DAC-∠EAC=5°.在△AOB中,∠BAO+∠ABO+∠AOB=180°,所以∠AOB=180°-∠BAO+∠ABO=180°-25°-35°=120°.
22.(1)解:EF=BE+DF.理由如下:在△ABE和△ADG中,因为AB=AD,∠B=∠ADG,BE=DG,所以△ABE≌△ADG,所以AE=AG,∠BAE=∠DAG. 因为∠EAF=false∠BAD,所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,所以∠EAF=∠GAF.在△AEF和△AGF中,因为AE=AG,∠EAF=∠GAF,AF=AF,所以△AEF≌
△AGF,所以EF=GF.因为GF=DG+DF=BE+DF,所以EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立.理由如下:如图2,延长FD到点G,使得DG=BE,连接AG.因为∠B+∠ADF=180°,∠ADG+∠ADF=180°,所以∠B=∠ADG.在△ABE和△ADG中,因为AB=AD,∠B=∠ADG,BE=DG,所以△ABE≌△ADG,所以AE=AG,∠BAE=∠DAG.因为∠EAF=false∠BAD,所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,所以∠EAF=∠GAF. 在△AEF和△AGF中,因为AE=AG,∠EAF=∠GAF,AF=AF,所以△AEF≌△AGF,所以EF=GF.因为GF=DG+DF=BE+DF,所以EF=BE+DF.
图2 图3
23.解:(1)测量工具:测角仪,卷尺;
(2)测量的示意图如图3所示,测量步骤:
①在公路false上选取两点A,C,用测角仪测得∠BAC=90°,∠ACB=α;
②在公路false的草地一侧过点C作射线CP,使∠ACP=∠ACB=α,CP交BA的延长线于点D;
③用卷尺测出AD的长,记为a m,则点B到公路false的距离即为a m.
(3)在△ABC和△ADC中,因为∠BAC=∠DAC,AC=AC,∠ACB=∠ACD,所以△ABC
≌△ADC,所以AB=AD=a m,即点B到公路false的距离为a m.
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列图形与图1中的图形是全等形的是( )
A B C D 图1
2.用尺规作图,已知三边作三角形,用到的基本作图是( )
A.作一个角等于已知角 B.作已知直线的垂线
C.作一条线段等于已知线段 D.作角的平分线
3.用三角尺作△ABC的边BC上的高时,下列三角尺的摆放位置正确的是( )
A B C D
4.如图2,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( ) x
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB=OA
图2
图3 图4
5.如图3,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
6.小红用图4所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,BO=OC,CD⊥BC,点A,O,D在同一条直线上,就能保证△ABO≌△DCO,从而可通过测量CD的长度得知小河的宽度AB.在这个问题中,可作为证明△ABO≌△DCO的依据的是( )
A.SAS或SSS B.AAS或SSS C.ASA或AAS D.ASA或SAS
7.如图5,D是△ABC的角平分线BD和CD的交点,若∠A=50°,则∠D的度数为( )
A.120° B.130° C.115° D.110°
图5 图6
8.图6中的a,b,c分别为三角形的三边长,则甲、乙、丙三个三角形和左侧△ABC一定全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
9.如图7,在正方形网格内(每个小正方形的边长为1),有一格点三角形ABC(三个顶点分别在正方形网格的格点上),现需要在网格内构造一个新的格点三角形与原三角形全等,且有一条边与原三角形的一条边重合,这样的三角形可以构造出( )
A.3个 B.4个 C.5个 D.6个
图7 图8
10.如图8,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BDC=180°;③AD=EC;④AC=2CD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题3分,共18分)
11.赵师傅在做完门框后,为防止变形,如图9中所示的那样在门上钉上两条斜拉的木条(即
图中的AB,CD两根木条),其中的数学原理是 .
图9 图10 图11
12.如图10,△ACF≌△DBE,若AD=11,BC=3,则线段AB的长为 .
13.已知∠α和线段a,用尺规作△ABC,使∠A=2∠α,AB=2a,∠B=3∠α,作法如下:①在AN上截取AB=2a,②作∠MAN=2∠α,③以B为圆心,BA为一边作∠ABE=3∠α,BE交AM于点C,△ABC就是所求作的三角形.以上正确的作图顺序是 .(填序号)
14.把长度为9的铁丝截成三段,围成三条边互不相等的三角形,且三边长均为整数,那么这三边长分别为 .
15.如图11,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4 cm2,则阴影部分的面积为 cm2.
16.如图12,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么按照图中所标注的数据,图中实线所围成的图形面积为 .
图12
三、解答题(本大题共6小题,共52分)
17.(6分)如图13,AD⊥AE,AB⊥AC,AD=AE,AB=AC.试说明:△ABD≌△ACE.
图13 图14
18.(6分)如图14,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,∠FEC=30°,求∠EAF的度数.
19.(8分)已知△ABC的三边长分别为a,b,c,且满足a=b+2,b=c+1.
(1)试说明:b一定大于3;
(2)若这个三角形周长为22,求a,b,c.
20.(10分)如图15,在△ABC中,BD⊥AC,垂足为点D,且∠A<∠C,点E是一动点,其在BC上移动,连接DE,并过点E作EF⊥DE,点F在AB的延长线上,连接DF交BC于点G.
(1)请同学们根据以上提示,在图15的基础上补全示意图.
(2)当△ABD与△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠BFE的度数.
图15 图16
21.(10分)如图16,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.
22.(12分)【问题背景】
如图17,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,试探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先说明△ABE≌△ADG,再说明△AEF≌△AGF,可得出结论,他的结论应是 ,试说明理由;
【探索延伸】
如图18,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=false∠BAD,上述结论是否仍然成立,并说明理由.
附加题(20分,不计入总分)
23.如图19,河边有一条笔直的公路false,公路另一侧是平坦的草地,在数学活动课上,老师要求测量河对岸点B到公路的距离,请你设计一个测量方案.
(1)写出你所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤,并用字母表示测得的数据,求出点B到公路的距离;
(3)试说明你测量的正确性.
图19
第一章 三角形综合测评参考答案
一、1.B 2.C 3.A 4.D 5.C 6.C 7.C 8.B 9.C 10.C
二、11.三角形的稳定性 12.4 13.②①③ 14.2,3,4 15.1 16.40.5
三、17.解:因为AD⊥AE,AB⊥AC,所以∠CAB=∠DAE=90°,所以∠CAB+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.在△ABD和△ACE中,因为AB=AC,∠BAD=∠CAE,AD=AE,所以△ABD≌△ACE.
18.解:因为四边形ABCD是长方形,所以∠D=90°. 依题意,得△ADE≌△AFE,所以∠EFA=∠D=90°,∠AEF=∠AED. 因为∠AEF+∠AED+∠FEC=180°,所以∠AEF=false(180°-∠FEC)=false(180°-30°)=75°,所以∠EAF=90°-∠AEF=90°-75°=15°.
19.解:(1)因为a=b+2,b=c+1,所以b=a-2,b=c+1,所以a-2=c+1,a-c=3.根据三角形的任意两边之差小于第三边,可得a-c<b,所以b一定大于3.
(2)因为b=c+1,所以c=b-1,所以b+2+b+b-1=22,解得b=7,所以a=b+2=9,c=b-1=6.
20.解:(1)补全示意图如图1所示;
图1
(2)因为DE⊥EF,BD⊥AC,所以∠DEF=∠ADB=90°.因为△ABD与△FDE全等,且AD=FE,所以∠ABD=∠FDE.在Rt△ABD中,∠ABD=90°-∠A=60°,所以∠FDE=60°.在Rt△FED中,∠DFE=90°-∠FDE=90°-60°=30°.所以∠BFE=∠BFD+∠DFE=40°+30°=70°.
21.解:因为∠CAB=50°,∠C=60°,所以∠ABC=180°-50°-60°=70°.因为AD是高,所以∠ADC=90°,所以∠DAC=90°-∠C=30°.因为AE,BF是角平分线,所以∠CBF=∠ABF=35°,∠EAC=∠EAB=25°,所以∠DAE=∠DAC-∠EAC=5°.在△AOB中,∠BAO+∠ABO+∠AOB=180°,所以∠AOB=180°-∠BAO+∠ABO=180°-25°-35°=120°.
22.(1)解:EF=BE+DF.理由如下:在△ABE和△ADG中,因为AB=AD,∠B=∠ADG,BE=DG,所以△ABE≌△ADG,所以AE=AG,∠BAE=∠DAG. 因为∠EAF=false∠BAD,所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,所以∠EAF=∠GAF.在△AEF和△AGF中,因为AE=AG,∠EAF=∠GAF,AF=AF,所以△AEF≌
△AGF,所以EF=GF.因为GF=DG+DF=BE+DF,所以EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立.理由如下:如图2,延长FD到点G,使得DG=BE,连接AG.因为∠B+∠ADF=180°,∠ADG+∠ADF=180°,所以∠B=∠ADG.在△ABE和△ADG中,因为AB=AD,∠B=∠ADG,BE=DG,所以△ABE≌△ADG,所以AE=AG,∠BAE=∠DAG.因为∠EAF=false∠BAD,所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,所以∠EAF=∠GAF. 在△AEF和△AGF中,因为AE=AG,∠EAF=∠GAF,AF=AF,所以△AEF≌△AGF,所以EF=GF.因为GF=DG+DF=BE+DF,所以EF=BE+DF.
图2 图3
23.解:(1)测量工具:测角仪,卷尺;
(2)测量的示意图如图3所示,测量步骤:
①在公路false上选取两点A,C,用测角仪测得∠BAC=90°,∠ACB=α;
②在公路false的草地一侧过点C作射线CP,使∠ACP=∠ACB=α,CP交BA的延长线于点D;
③用卷尺测出AD的长,记为a m,则点B到公路false的距离即为a m.
(3)在△ABC和△ADC中,因为∠BAC=∠DAC,AC=AC,∠ACB=∠ACD,所以△ABC
≌△ADC,所以AB=AD=a m,即点B到公路false的距离为a m.
