平行四边形的性质
图片预览



文档简介
(共15张PPT)
授课教师:郑海兵
沪科版八年级下
请留意生活中的图形
问题1:
什么是平行四边形?
问题2:
平行四边形都有那些性质?
问题3:
这些性质用符号语言如何表示 并如何应用这些性质解决实际问题?
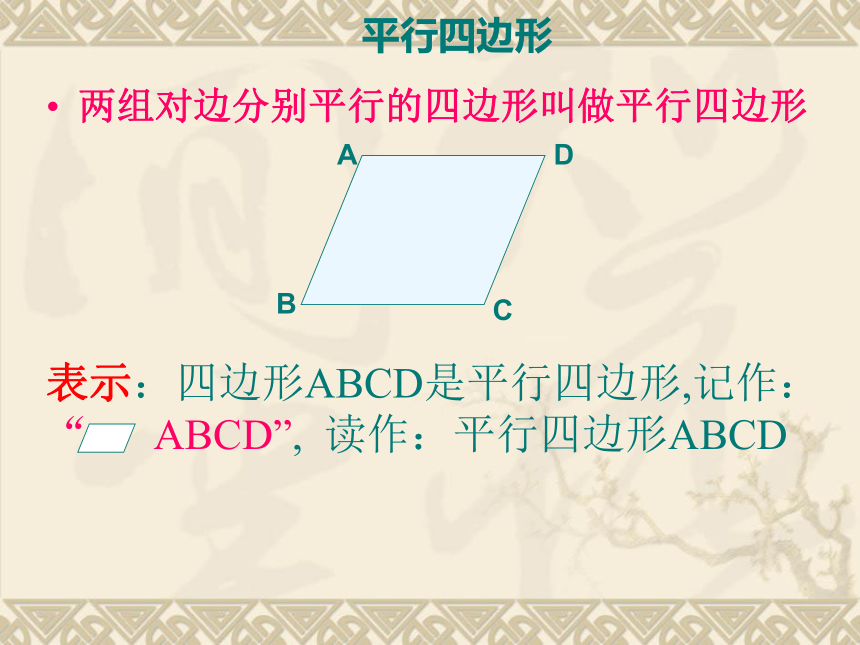
两组对边分别平行的四边形叫做平行四边形
表示:四边形ABCD是平行四边形,记作: “ ABCD”, 读作:平行四边形ABCD
A
B
C
D
平行四边形
C
O
B
D
A
o
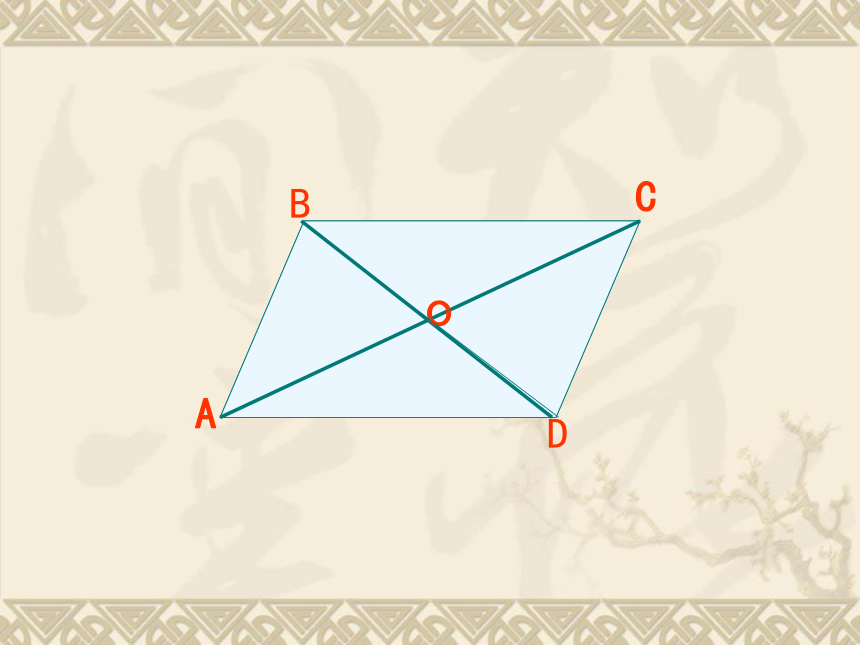
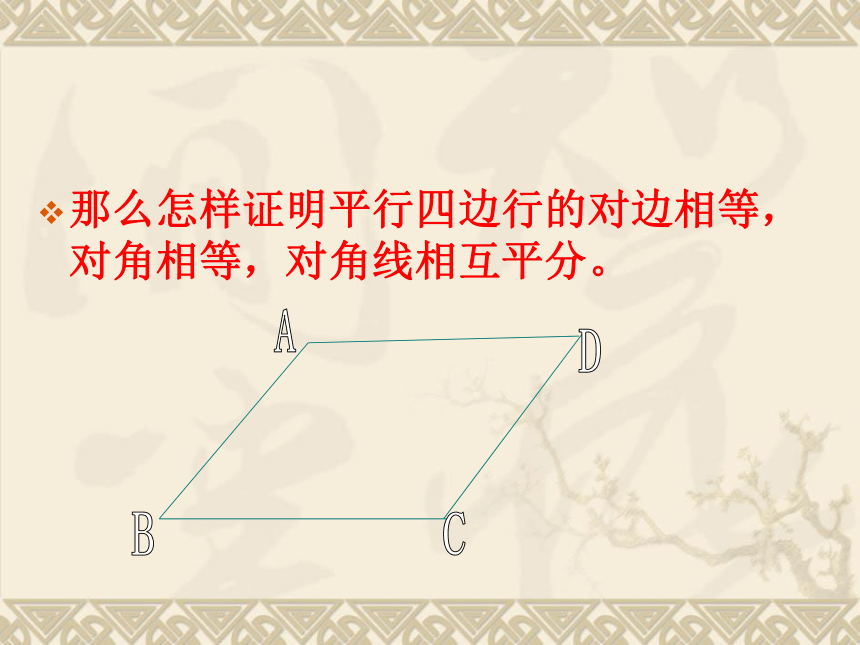
那么怎样证明平行四边行的对边相等,对角相等,对角线相互平分。
平行四边形的性质
A
D
C
B
平行
且相等
相等
互补
∠A=∠C,∠B=∠D
∠A+∠B=180°
互相平分
AO=CO BO=DO
O
B
A
C
D
AB∥CD,AD∥BC
=
=
已知 ABCD中,∠A=80°,你能求出其他各角的度数吗?说说你的理由。
说一说1
∠C=80°
∠D=100°
∠B=100°
在 ABCD 中, ∠A=48°,BC=3cm,则∠B= , ∠C= ,AD= 。
说一说2
问题1 :已知平行四边行ABCD相邻两个角的度数比为2 :3,求平行四边行的各内角的度数。
A
B
C
D
∵四边形ABCD是平行四边形
解:
∴ ∠A + ∠B = 180 。 ∠A = ∠c, ∠B = ∠D
又∵相邻的两个角比为2:3,则设 ∠A =2X,∠B =3X
于是2X+3X=180 。
。
∴ ∠ A = ∠c =2x=72。, ∠B =∠D= 3x=108 。
解得X=36。
问题2 :已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
连结AC,已知 ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
课堂小结
1 平行四边形的定义
2 平行四边形的三条性质
作业
课堂练习:课本 P76:1,2,3。
课后作业;P80习题20.2第一题,和上面练习。
授课教师:郑海兵
沪科版八年级下
请留意生活中的图形
问题1:
什么是平行四边形?
问题2:
平行四边形都有那些性质?
问题3:
这些性质用符号语言如何表示 并如何应用这些性质解决实际问题?
两组对边分别平行的四边形叫做平行四边形
表示:四边形ABCD是平行四边形,记作: “ ABCD”, 读作:平行四边形ABCD
A
B
C
D
平行四边形
C
O
B
D
A
o
那么怎样证明平行四边行的对边相等,对角相等,对角线相互平分。
平行四边形的性质
A
D
C
B
平行
且相等
相等
互补
∠A=∠C,∠B=∠D
∠A+∠B=180°
互相平分
AO=CO BO=DO
O
B
A
C
D
AB∥CD,AD∥BC
=
=
已知 ABCD中,∠A=80°,你能求出其他各角的度数吗?说说你的理由。
说一说1
∠C=80°
∠D=100°
∠B=100°
在 ABCD 中, ∠A=48°,BC=3cm,则∠B= , ∠C= ,AD= 。
说一说2
问题1 :已知平行四边行ABCD相邻两个角的度数比为2 :3,求平行四边行的各内角的度数。
A
B
C
D
∵四边形ABCD是平行四边形
解:
∴ ∠A + ∠B = 180 。 ∠A = ∠c, ∠B = ∠D
又∵相邻的两个角比为2:3,则设 ∠A =2X,∠B =3X
于是2X+3X=180 。
。
∴ ∠ A = ∠c =2x=72。, ∠B =∠D= 3x=108 。
解得X=36。
问题2 :已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
连结AC,已知 ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
课堂小结
1 平行四边形的定义
2 平行四边形的三条性质
作业
课堂练习:课本 P76:1,2,3。
课后作业;P80习题20.2第一题,和上面练习。
