高中物理必修二 匀速圆周运动的向心力和向心加速度课件21张PPT
文档属性
| 名称 | 高中物理必修二 匀速圆周运动的向心力和向心加速度课件21张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-07 00:00:00 | ||
图片预览








文档简介
第二章 匀速圆周运动
2.3-2.4 圆周运动的实例分析 圆周运动与人类文明(选学)
学习目标定位
进一步理解圆周运动的规律,在具体问题中会分析向心
力的来源.
会求非匀速圆周运动中物体在特殊点的向心力和向心
加速度.
知道离心现象,会根据离心运动的条件判断物体的运
动,了解离心运动的应用和防止.
了解圆周运动在人类文明进程中的广泛应用,认识圆
周运动对人类文明发展的重大影响.
学习探究区
一、汽车过拱形桥
二、“旋转秋千”
三、火车转弯
一、汽车过拱形桥
1.质量为m的汽车在拱形桥上以速度v行驶,若桥面的圆弧半径为R,试画出汽车受力分析图,并求出汽车通过桥的最高点时对桥的压力.汽车的重力与汽车对桥的压力谁大?
问题设计
答案
由牛顿第二定律
由牛顿第三定律,对桥的压力N′=N<mg
mg
N
压力随汽车速度的增大而减小
一、汽车过拱形桥
2.当汽车通过凹形桥最低点时,汽车对桥的压力比汽车的重力大还是小呢?请同学们自己分析.
问题设计
答案 受力分析如图
mg
N
由牛顿第二定律
压力随汽车速度的增大而增大
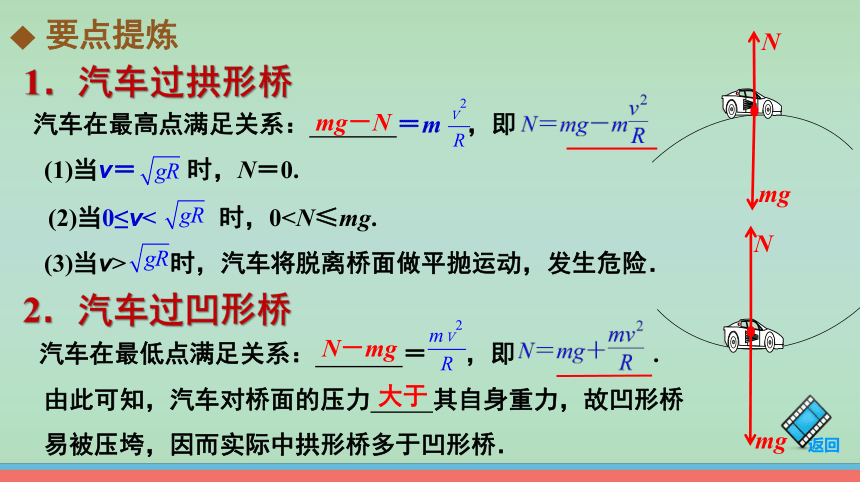
要点提炼
1.汽车过拱形桥
mg-N
mg
N
2.汽车过凹形桥
由此可知,汽车对桥面的压力 其自身重力,故凹形桥易被压垮,因而实际中拱形桥多于凹形桥.
(1)当v= 时,N=0.
(2)当0≤v< 时,0(3)当v> 时,汽车将脱离桥面做平抛运动,发生危险.
汽车在最高点满足关系: =m ,即
mg
N
N-mg
汽车在最低点满足关系: = ,即 .
大于
返回
二、“旋转秋千”
“旋转秋千”的运动可简化为圆锥摆模型,当小球在水平面内做圆周运动时,回答下列问题:
(1)小球受到几个力的作用?什么力提供小球做圆周运动的向心力?
(2)小球在水平方向上有无加速度?在竖直方向有无加速度?
(3)“旋转秋千”缆绳与中心轴的夹角与所乘坐人的质量有关吗?
问题设计
答案 (1)如图所示,绳子的拉力和重力的合力提供向心力
mg
T
(2)水平有向心加速度;
(3)F合=mgtanα ①
合力为零,加速度为零
竖直无加速度
由牛顿第二定律得 F合=mω2r ③
联立①②③得 cosα =
α只与角速度和绳长有关,与质量无关
α
要点提炼
返回
1.向心力:
做圆锥摆运动的小球在水平面内做匀速圆周运动的向心力是由其受到的重力和悬线拉力T的合力F合提供,即F合=_______
mgtan α
2.动力学方程:
mgtan α=mω2 _____
lsin α
3.圆锥摆的周期
三、火车转弯
火车转弯时的运动是圆周运动,分析火车的运动回答下列问题:
问题设计
(1)如图所示,如果轨道是水平的,火车转弯时受到哪些力的作用?需要的向心力由谁来提供?
答案 轨道水平时,火车受力如图:
mg
N
F弹
f
提供向心力
向心力由轨道对轮缘的弹力来提供.
三、火车转弯
火车转弯时的运动是圆周运动,分析火车的运动回答下列问题:
问题设计
(2)(1)中获得向心力的方法好不好?为什么?若不好,如何改进?
轮缘与外轨的相互作用力很大,铁轨和车轮极易受损.
mg
N
F弹
f
提供向心力
答案 这种方法不好;
火车质量大,速度大,需要的向心力F向=mv2/r较大
改进方法:
在转弯处使外轨略高于内轨
支持力和重力的合力可以提供一部分向心力
三、火车转弯
火车转弯时的运动是圆周运动,分析火车的运动回答下列问题:
问题设计
(3)当轨道平面与水平面之间的夹角为α,转弯半径为R时,火车行驶速度多大轨道才不受挤压?
答案 (3)火车受力如图所示,则
所以v=
要点提炼
1.向心力来源:
在铁路转弯处,内、外铁轨有高度差,火车在此处依据规定的速度行驶,转弯时,向心力几乎完全由 和 的合力提供,即F= .
(1)当v=v0时,F=F合,即转弯时所需向心力等于支持力和重力的合力,
这时内、外轨 ,这就是设计的限速状态.
2.规定速度:
支持力N
重力G
内轨
均无侧压力
(2)当v>v0时,F>F合,即所需向心力大于支持力和重力的合力,这时_____
对车轮有侧压力,以弥补向心力不足的部分.
(3)当v 对车轮有侧压力,以抵消向心力过大的部分.
mgtanα
外轨
若火车转弯时,火车轮缘不受轨道压力,则mgtanα= ,故v0= ,其中R为弯道半径,α为轨道所在平面与水平面的夹角,v0为弯道规定的速度.
返回
例1 一辆质量m=2 t的轿车,驶过半径R=90 m的一段凸形桥面,g=10 m/s2,求:
(1)轿车以10 m/s的速度通过桥面最高点时,对桥面的压力是多大?
(2)在最高点对桥面的压力等于轿车重力的一半时,车的速度大小是多少?
典例精析
一、汽车过拱形桥问题
圆周运动
支持力?
(1)轿车在最高点
解析
根据牛顿第三定律,轿车对桥面压力为1.78×104 N
(2)
返回
N
例2 如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面做匀速圆周运动,以下物理量大小关系正确的是( )
A.速度vA>vB
B.角速度ωA>ωB
C.向心力FA>FB
D.向心加速度aA>aB
典例精析
二、圆锥摆模型
返回
G
N
解析 设漏斗的顶角为2θ
F合
小球的合力为
aA=aB
rA>rB
vA>vB、
ωA<ωB
A
三、火车转弯
典例精析
例3 铁路在弯道处的内、外轨道高度是不同的,已知内、外轨道平面与水平面的夹角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于 ,则( )
A.内轨对内侧车轮轮缘有挤压
B.外轨对外侧车轮轮缘有挤压
C.这时铁轨对火车的支持力等于
D.这时铁轨对火车的支持力大于
C
返回
假如火车只受重力和支持力
N
例4 如图所示,高速公路转弯处弯道圆半径R=100 m,汽车轮胎与路面间的动摩擦因数μ=0.23.最大静摩擦力与滑动摩擦力相等,若路面是水平的,问汽车转弯时不发生径向滑动(离心现象)所许可的最大速率vm为多大?当超过vm 时,将会出现什么现象?(g=9.8 m/s2)
典例精析
解析
四、对离心运动的理解
转弯时,静摩擦力提供向心力
汽车将做离心运动
返回
N
f
课堂要点小结
生活中的圆周运动
车过拱形桥
火车转弯
重力与支持力的合力提供向心力
外轨高于内轨
旋转秋千
离心运动
拱形桥最高点
凹形桥最低点
返回
自我检测区
1
2
3
1. (交通工具的转弯问题)汽车在水平地面上转弯时,地面的摩擦力已达到最大,当汽车速率增为原来的2倍时,若要不发生险情,则汽车转弯的轨道半径必须( )
A.减为原来的
B.减为原来的
C.增为原来的2倍
D.增为原来的4倍
D
速率增加前:
速率增加后:
1
2
3
1
2
3
2. (圆锥摆模型)两个质量相同的小球,在同一水平面内做匀速圆周运动,悬点相同,如图所示,A运动的半径比B的大,则( )
A.A所需的向心力比B的大
B.B所需的向心力比A的大
C.A的角速度比B的大
D.B的角速度比A的大
两球受力雷同
两球受力雷同
解析
T
1
2
3
3. (对离心运动的理解)如图所示,光滑水平面上,质量为m的小球在拉力F作用下做匀速圆周运动.若小球运动到P点时,拉力F发生变化,下列关于小球运动情况的说法中正确的是( )
A.若拉力突然变大,小球将沿轨迹Pb做
离心运动
B.若拉力突然变小,小球将沿轨迹Pb做
离心运动
C.若拉力突然消失,小球将沿轨迹Pa做
离心运动
D.若拉力突然变小,小球将沿轨迹Pc做
近心运动
匀速圆周运动
近心运动
离心运动
保持匀速直线
惯性
2.3-2.4 圆周运动的实例分析 圆周运动与人类文明(选学)
学习目标定位
进一步理解圆周运动的规律,在具体问题中会分析向心
力的来源.
会求非匀速圆周运动中物体在特殊点的向心力和向心
加速度.
知道离心现象,会根据离心运动的条件判断物体的运
动,了解离心运动的应用和防止.
了解圆周运动在人类文明进程中的广泛应用,认识圆
周运动对人类文明发展的重大影响.
学习探究区
一、汽车过拱形桥
二、“旋转秋千”
三、火车转弯
一、汽车过拱形桥
1.质量为m的汽车在拱形桥上以速度v行驶,若桥面的圆弧半径为R,试画出汽车受力分析图,并求出汽车通过桥的最高点时对桥的压力.汽车的重力与汽车对桥的压力谁大?
问题设计
答案
由牛顿第二定律
由牛顿第三定律,对桥的压力N′=N<mg
mg
N
压力随汽车速度的增大而减小
一、汽车过拱形桥
2.当汽车通过凹形桥最低点时,汽车对桥的压力比汽车的重力大还是小呢?请同学们自己分析.
问题设计
答案 受力分析如图
mg
N
由牛顿第二定律
压力随汽车速度的增大而增大
要点提炼
1.汽车过拱形桥
mg-N
mg
N
2.汽车过凹形桥
由此可知,汽车对桥面的压力 其自身重力,故凹形桥易被压垮,因而实际中拱形桥多于凹形桥.
(1)当v= 时,N=0.
(2)当0≤v< 时,0
汽车在最高点满足关系: =m ,即
mg
N
N-mg
汽车在最低点满足关系: = ,即 .
大于
返回
二、“旋转秋千”
“旋转秋千”的运动可简化为圆锥摆模型,当小球在水平面内做圆周运动时,回答下列问题:
(1)小球受到几个力的作用?什么力提供小球做圆周运动的向心力?
(2)小球在水平方向上有无加速度?在竖直方向有无加速度?
(3)“旋转秋千”缆绳与中心轴的夹角与所乘坐人的质量有关吗?
问题设计
答案 (1)如图所示,绳子的拉力和重力的合力提供向心力
mg
T
(2)水平有向心加速度;
(3)F合=mgtanα ①
合力为零,加速度为零
竖直无加速度
由牛顿第二定律得 F合=mω2r ③
联立①②③得 cosα =
α只与角速度和绳长有关,与质量无关
α
要点提炼
返回
1.向心力:
做圆锥摆运动的小球在水平面内做匀速圆周运动的向心力是由其受到的重力和悬线拉力T的合力F合提供,即F合=_______
mgtan α
2.动力学方程:
mgtan α=mω2 _____
lsin α
3.圆锥摆的周期
三、火车转弯
火车转弯时的运动是圆周运动,分析火车的运动回答下列问题:
问题设计
(1)如图所示,如果轨道是水平的,火车转弯时受到哪些力的作用?需要的向心力由谁来提供?
答案 轨道水平时,火车受力如图:
mg
N
F弹
f
提供向心力
向心力由轨道对轮缘的弹力来提供.
三、火车转弯
火车转弯时的运动是圆周运动,分析火车的运动回答下列问题:
问题设计
(2)(1)中获得向心力的方法好不好?为什么?若不好,如何改进?
轮缘与外轨的相互作用力很大,铁轨和车轮极易受损.
mg
N
F弹
f
提供向心力
答案 这种方法不好;
火车质量大,速度大,需要的向心力F向=mv2/r较大
改进方法:
在转弯处使外轨略高于内轨
支持力和重力的合力可以提供一部分向心力
三、火车转弯
火车转弯时的运动是圆周运动,分析火车的运动回答下列问题:
问题设计
(3)当轨道平面与水平面之间的夹角为α,转弯半径为R时,火车行驶速度多大轨道才不受挤压?
答案 (3)火车受力如图所示,则
所以v=
要点提炼
1.向心力来源:
在铁路转弯处,内、外铁轨有高度差,火车在此处依据规定的速度行驶,转弯时,向心力几乎完全由 和 的合力提供,即F= .
(1)当v=v0时,F=F合,即转弯时所需向心力等于支持力和重力的合力,
这时内、外轨 ,这就是设计的限速状态.
2.规定速度:
支持力N
重力G
内轨
均无侧压力
(2)当v>v0时,F>F合,即所需向心力大于支持力和重力的合力,这时_____
对车轮有侧压力,以弥补向心力不足的部分.
(3)当v
mgtanα
外轨
若火车转弯时,火车轮缘不受轨道压力,则mgtanα= ,故v0= ,其中R为弯道半径,α为轨道所在平面与水平面的夹角,v0为弯道规定的速度.
返回
例1 一辆质量m=2 t的轿车,驶过半径R=90 m的一段凸形桥面,g=10 m/s2,求:
(1)轿车以10 m/s的速度通过桥面最高点时,对桥面的压力是多大?
(2)在最高点对桥面的压力等于轿车重力的一半时,车的速度大小是多少?
典例精析
一、汽车过拱形桥问题
圆周运动
支持力?
(1)轿车在最高点
解析
根据牛顿第三定律,轿车对桥面压力为1.78×104 N
(2)
返回
N
例2 如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面做匀速圆周运动,以下物理量大小关系正确的是( )
A.速度vA>vB
B.角速度ωA>ωB
C.向心力FA>FB
D.向心加速度aA>aB
典例精析
二、圆锥摆模型
返回
G
N
解析 设漏斗的顶角为2θ
F合
小球的合力为
aA=aB
rA>rB
vA>vB、
ωA<ωB
A
三、火车转弯
典例精析
例3 铁路在弯道处的内、外轨道高度是不同的,已知内、外轨道平面与水平面的夹角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于 ,则( )
A.内轨对内侧车轮轮缘有挤压
B.外轨对外侧车轮轮缘有挤压
C.这时铁轨对火车的支持力等于
D.这时铁轨对火车的支持力大于
C
返回
假如火车只受重力和支持力
N
例4 如图所示,高速公路转弯处弯道圆半径R=100 m,汽车轮胎与路面间的动摩擦因数μ=0.23.最大静摩擦力与滑动摩擦力相等,若路面是水平的,问汽车转弯时不发生径向滑动(离心现象)所许可的最大速率vm为多大?当超过vm 时,将会出现什么现象?(g=9.8 m/s2)
典例精析
解析
四、对离心运动的理解
转弯时,静摩擦力提供向心力
汽车将做离心运动
返回
N
f
课堂要点小结
生活中的圆周运动
车过拱形桥
火车转弯
重力与支持力的合力提供向心力
外轨高于内轨
旋转秋千
离心运动
拱形桥最高点
凹形桥最低点
返回
自我检测区
1
2
3
1. (交通工具的转弯问题)汽车在水平地面上转弯时,地面的摩擦力已达到最大,当汽车速率增为原来的2倍时,若要不发生险情,则汽车转弯的轨道半径必须( )
A.减为原来的
B.减为原来的
C.增为原来的2倍
D.增为原来的4倍
D
速率增加前:
速率增加后:
1
2
3
1
2
3
2. (圆锥摆模型)两个质量相同的小球,在同一水平面内做匀速圆周运动,悬点相同,如图所示,A运动的半径比B的大,则( )
A.A所需的向心力比B的大
B.B所需的向心力比A的大
C.A的角速度比B的大
D.B的角速度比A的大
两球受力雷同
两球受力雷同
解析
T
1
2
3
3. (对离心运动的理解)如图所示,光滑水平面上,质量为m的小球在拉力F作用下做匀速圆周运动.若小球运动到P点时,拉力F发生变化,下列关于小球运动情况的说法中正确的是( )
A.若拉力突然变大,小球将沿轨迹Pb做
离心运动
B.若拉力突然变小,小球将沿轨迹Pb做
离心运动
C.若拉力突然消失,小球将沿轨迹Pa做
离心运动
D.若拉力突然变小,小球将沿轨迹Pc做
近心运动
匀速圆周运动
近心运动
离心运动
保持匀速直线
惯性
