七年级数学直方图
图片预览








文档简介
(共28张PPT)
10、2直方图(1)
西葛中学
董杰文
一、教材分析:
对于直方图,学生在前两个学段没有接触,这是本学段
学习的一种新统计图。教科书从学生熟悉的问题情景入手:
从63名学生中选出40名参加广播体操比赛。选择参赛队员
的一个要求是队员的身高应尽可能整齐。我们可以用不同
的方法选出符合这个要求的队员,教科书介绍了利用频数
分布确定人选的方法。分析数据的频数分布,首先是将
数据分组,根据一组数据的最大值、最小值可以确定这组
数据的极差,极差反映了数据的变化范围。参照极差,
可以确定组距,进而可以将数据进行分组,利用频数
分布表给出了身高数据的分布情况,分析频数分布表
可以看出大部分学生的身高分布在哪个范围,由此可以
确定参赛选手的身高。
对于连续性数据(如身高),分组后可以用频数
分布直方图来描述频数分布的情况,教科书介绍了
根据频数分布表做出频数分布直方图的方法,以及
根据频数分布直方图和频数分布表作出频数分布
折线图的方法。教科书这样安排,是结合一个实际
问题介绍了如何利用直方图描述数据的方法,
从而使得对于统计图表的认识具体化。
二、教学目标:
1、了解频数及频数分布,掌握划记法,
会用表格整理数据表示频数分布,体会
表格在整理数据中的作用。
2、鼓励学生自主探索、合作交流,
意识到与同伴交流合作的重要性.
教学重点:组距和组数、频数及频数分布表
教学难点:决定组距和组数
解决重难点的方法:
1、从解决实际问题的需要出发,
根据频数分布直方图的特点和作用,
学习制作这种统计图的方法。
2、结合具体问题,使学生在具体
情境中感知频数、频数分布等概念。
三.学生分析
通过前两节课的学习学生对数据的收集与整理
已经有了初步的认识在此基础上研究讨论一种
新的统计图----直方图,对后继学习产生积极影响。
学生通过自学将更进一步了解统计学,对学生以后
学习打下良好的基础。
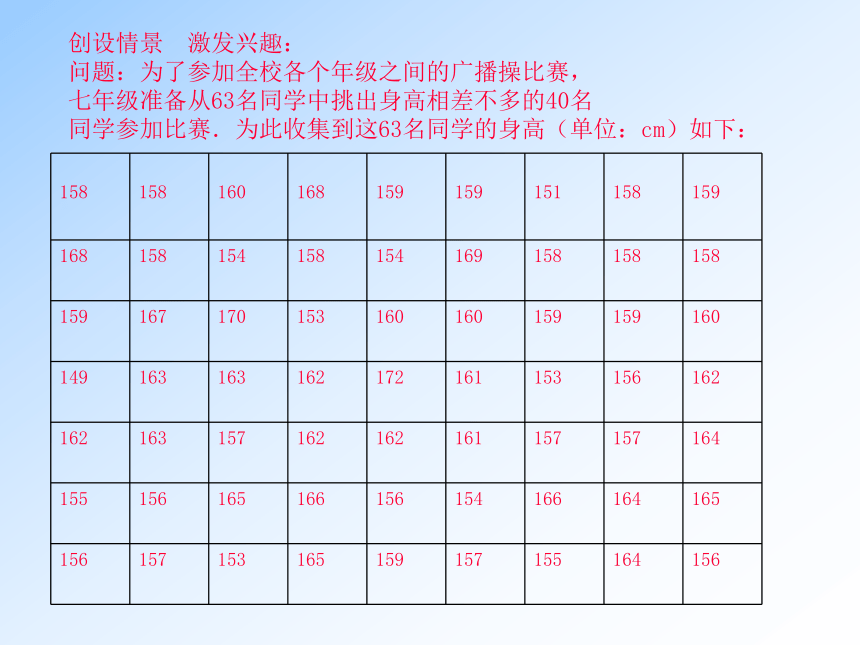
创设情景 激发兴趣:
问题:为了参加全校各个年级之间的广播操比赛,
七年级准备从63名同学中挑出身高相差不多的40名
同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158
158
160
168
159
159
151
158
159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
G
教师提出问题,学生思考、交流,回答问题。
1.在测得的这组数据中,身高最高的是多少?
最矮是多少?相差多少?
2.这63名学生在哪个范围内变化?
3.选择身高在哪个范围的学生参加?
G
设计意图:
①此情景的设计可以激发学生的兴趣,
体会生活中的数学。
②通过问题串,减少难度,促使学生
主动参与到学习中来
③问题1中的身高最高目的是找最大值,
最矮目的是找最小值
问题1实质上是为问题2做铺垫,有了
问题1的基础,问题2就迎刃而解了
问题3给学生一个想象的空间,通过讨论
激发学生参与课堂学习的兴趣与热情.
合作交流 探索新知
阅读课本 P164 完成下列问题
1.什么是组距?什么是频数?
如何确定分组数?
2.归纳列频数分布表的步骤?
教师归纳总结,形成知识体系。
1.组距:把所有数据分成若干组,
每个小组的两个端点之间的距离
(组内数据的取值范围)
频数:对落在各个小组内的数据进行累计,
得到各个小组内的数据的个数
当数据在100个以内时,按照数据的多少,
常分成5-12组。
列频数分步表的步骤:
(1)计算最大值和最小值的差
(2)决定组距和组数(注意确定分界点,
遵循不重不漏,取低不取高的原则)
(3)列频数分布表
继续探究:
1、上面数据进行分组时,组距取2,求一下组数?
2、上面数据进行分组时,组距取4,求一下组数?
3、上面两种分组方法能否选出40名队员?
4、思考分组时,应该注意什么?
设计意图:
通过这些问题,使学生逐步体会在确定
组距时要注意组数的多少,组数过多
(组距过小)数据比较分散,组数过少
(组距过大)数据比较集中,无法解决
实际中的问题。分组时数据是100个左右时,
一般分成10组左右。
学以致用 :
1.为绘制一批数据的频数分布直方图,首先要
算出这批数据的变动范围是指数据的( )
A.最大值 B.最小值 C.个数 D.最大值与最小值的差
2.如果一组数据共有100个,则通常分成( )
A.3~5组 B.5~12组 C.12~20组 D.20~25组
3.某频数分布直方图中,共有A、B、C、D、E
五个小组,频数分布为10、15、25、35、10,
则直方图中,长方形高的比为( )
A.2﹕3﹕5﹕7﹕2 B.1﹕3﹕4﹕5﹕1
C.2﹕3﹕5﹕6﹕2 D.2﹕4﹕5﹕4﹕2
4.在频数分布直方图中,每个小长方形的面积等于( )
A.组距 B.组数 C.每组频数 D.以上都不对
5、超市为了制定某个时间段收
银台开放方案,统计了这个时间段
本超市顾客在收银台排队付款的
等待时间,并绘制成如下的频数分
布直方图.这个时间段内顾客等待
时间不少于6分钟的人数为( )
A.5人 B.7人 C.16人 D.44人
6.数字31 313 113 131 133 131 311中,
“1”的出现频数是 ,“3”出现的频数是 .
7.对某校同龄的的70名女学生的身高进行测量,
得到一组数据,其中最大值是169cm,最小值是146cm,
对这组数据进行整理时,可得到的极差
(最大值与最小值的差)为 ,如果确定它的组距
为3cm时,则组数为 .
8.如图所示,总共统计了 位学生的体重,体重段为
千克的学生最多,占总人数的百分比为 ,
如果体重为40~60千克属正常范围,那么体重属于正常
范围的学生占总体的百分比为 .(精确到0.1%)
9.下面是1998年参加国际教育评估的个国家学生的数学平均成绩(x)的统计图: (1)图 能很好地说明一半以上国家的学生成绩在60≤x < 70之间;
(2)图 能更好地说明学生成绩在70 ≤ x < 80的国家多于50 ≤ x < 60的国家.
作业:
1、某小区便民超市为了了解顾客的消费情况,
在该小区居民中进行调查,询问每户人家每周
到超市的次数,如图所示的图形是根据调查
结果绘制的,请问:(1)这种统计图通常被称为
什么统计图?
(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市
(4)请将这幅图改为扇形统计图.
2.某校18名数学老师的年龄(岁)如下:
29 42 58 37 53 52 49 24
37 42 55 40 38 50 26 54
26 44
请填写下列频数分布表:
年龄(x) 划记 频数
20≤x <30
30≤x <40
40≤x <50
50≤x <60
板书设计:10、2直方图(1)
列频数分步表的步骤:
(1)计算最大值和最小值的差
(2)决定组距和组数
(3)列频数分布表
10、2直方图(1)
西葛中学
董杰文
一、教材分析:
对于直方图,学生在前两个学段没有接触,这是本学段
学习的一种新统计图。教科书从学生熟悉的问题情景入手:
从63名学生中选出40名参加广播体操比赛。选择参赛队员
的一个要求是队员的身高应尽可能整齐。我们可以用不同
的方法选出符合这个要求的队员,教科书介绍了利用频数
分布确定人选的方法。分析数据的频数分布,首先是将
数据分组,根据一组数据的最大值、最小值可以确定这组
数据的极差,极差反映了数据的变化范围。参照极差,
可以确定组距,进而可以将数据进行分组,利用频数
分布表给出了身高数据的分布情况,分析频数分布表
可以看出大部分学生的身高分布在哪个范围,由此可以
确定参赛选手的身高。
对于连续性数据(如身高),分组后可以用频数
分布直方图来描述频数分布的情况,教科书介绍了
根据频数分布表做出频数分布直方图的方法,以及
根据频数分布直方图和频数分布表作出频数分布
折线图的方法。教科书这样安排,是结合一个实际
问题介绍了如何利用直方图描述数据的方法,
从而使得对于统计图表的认识具体化。
二、教学目标:
1、了解频数及频数分布,掌握划记法,
会用表格整理数据表示频数分布,体会
表格在整理数据中的作用。
2、鼓励学生自主探索、合作交流,
意识到与同伴交流合作的重要性.
教学重点:组距和组数、频数及频数分布表
教学难点:决定组距和组数
解决重难点的方法:
1、从解决实际问题的需要出发,
根据频数分布直方图的特点和作用,
学习制作这种统计图的方法。
2、结合具体问题,使学生在具体
情境中感知频数、频数分布等概念。
三.学生分析
通过前两节课的学习学生对数据的收集与整理
已经有了初步的认识在此基础上研究讨论一种
新的统计图----直方图,对后继学习产生积极影响。
学生通过自学将更进一步了解统计学,对学生以后
学习打下良好的基础。
创设情景 激发兴趣:
问题:为了参加全校各个年级之间的广播操比赛,
七年级准备从63名同学中挑出身高相差不多的40名
同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158
158
160
168
159
159
151
158
159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
G
教师提出问题,学生思考、交流,回答问题。
1.在测得的这组数据中,身高最高的是多少?
最矮是多少?相差多少?
2.这63名学生在哪个范围内变化?
3.选择身高在哪个范围的学生参加?
G
设计意图:
①此情景的设计可以激发学生的兴趣,
体会生活中的数学。
②通过问题串,减少难度,促使学生
主动参与到学习中来
③问题1中的身高最高目的是找最大值,
最矮目的是找最小值
问题1实质上是为问题2做铺垫,有了
问题1的基础,问题2就迎刃而解了
问题3给学生一个想象的空间,通过讨论
激发学生参与课堂学习的兴趣与热情.
合作交流 探索新知
阅读课本 P164 完成下列问题
1.什么是组距?什么是频数?
如何确定分组数?
2.归纳列频数分布表的步骤?
教师归纳总结,形成知识体系。
1.组距:把所有数据分成若干组,
每个小组的两个端点之间的距离
(组内数据的取值范围)
频数:对落在各个小组内的数据进行累计,
得到各个小组内的数据的个数
当数据在100个以内时,按照数据的多少,
常分成5-12组。
列频数分步表的步骤:
(1)计算最大值和最小值的差
(2)决定组距和组数(注意确定分界点,
遵循不重不漏,取低不取高的原则)
(3)列频数分布表
继续探究:
1、上面数据进行分组时,组距取2,求一下组数?
2、上面数据进行分组时,组距取4,求一下组数?
3、上面两种分组方法能否选出40名队员?
4、思考分组时,应该注意什么?
设计意图:
通过这些问题,使学生逐步体会在确定
组距时要注意组数的多少,组数过多
(组距过小)数据比较分散,组数过少
(组距过大)数据比较集中,无法解决
实际中的问题。分组时数据是100个左右时,
一般分成10组左右。
学以致用 :
1.为绘制一批数据的频数分布直方图,首先要
算出这批数据的变动范围是指数据的( )
A.最大值 B.最小值 C.个数 D.最大值与最小值的差
2.如果一组数据共有100个,则通常分成( )
A.3~5组 B.5~12组 C.12~20组 D.20~25组
3.某频数分布直方图中,共有A、B、C、D、E
五个小组,频数分布为10、15、25、35、10,
则直方图中,长方形高的比为( )
A.2﹕3﹕5﹕7﹕2 B.1﹕3﹕4﹕5﹕1
C.2﹕3﹕5﹕6﹕2 D.2﹕4﹕5﹕4﹕2
4.在频数分布直方图中,每个小长方形的面积等于( )
A.组距 B.组数 C.每组频数 D.以上都不对
5、超市为了制定某个时间段收
银台开放方案,统计了这个时间段
本超市顾客在收银台排队付款的
等待时间,并绘制成如下的频数分
布直方图.这个时间段内顾客等待
时间不少于6分钟的人数为( )
A.5人 B.7人 C.16人 D.44人
6.数字31 313 113 131 133 131 311中,
“1”的出现频数是 ,“3”出现的频数是 .
7.对某校同龄的的70名女学生的身高进行测量,
得到一组数据,其中最大值是169cm,最小值是146cm,
对这组数据进行整理时,可得到的极差
(最大值与最小值的差)为 ,如果确定它的组距
为3cm时,则组数为 .
8.如图所示,总共统计了 位学生的体重,体重段为
千克的学生最多,占总人数的百分比为 ,
如果体重为40~60千克属正常范围,那么体重属于正常
范围的学生占总体的百分比为 .(精确到0.1%)
9.下面是1998年参加国际教育评估的个国家学生的数学平均成绩(x)的统计图: (1)图 能很好地说明一半以上国家的学生成绩在60≤x < 70之间;
(2)图 能更好地说明学生成绩在70 ≤ x < 80的国家多于50 ≤ x < 60的国家.
作业:
1、某小区便民超市为了了解顾客的消费情况,
在该小区居民中进行调查,询问每户人家每周
到超市的次数,如图所示的图形是根据调查
结果绘制的,请问:(1)这种统计图通常被称为
什么统计图?
(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市
(4)请将这幅图改为扇形统计图.
2.某校18名数学老师的年龄(岁)如下:
29 42 58 37 53 52 49 24
37 42 55 40 38 50 26 54
26 44
请填写下列频数分布表:
年龄(x) 划记 频数
20≤x <30
30≤x <40
40≤x <50
50≤x <60
板书设计:10、2直方图(1)
列频数分步表的步骤:
(1)计算最大值和最小值的差
(2)决定组距和组数
(3)列频数分布表
