人教版八年级数学上册课时练 :14.2 乘法公式(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册课时练 :14.2 乘法公式(Word版 含答案) | 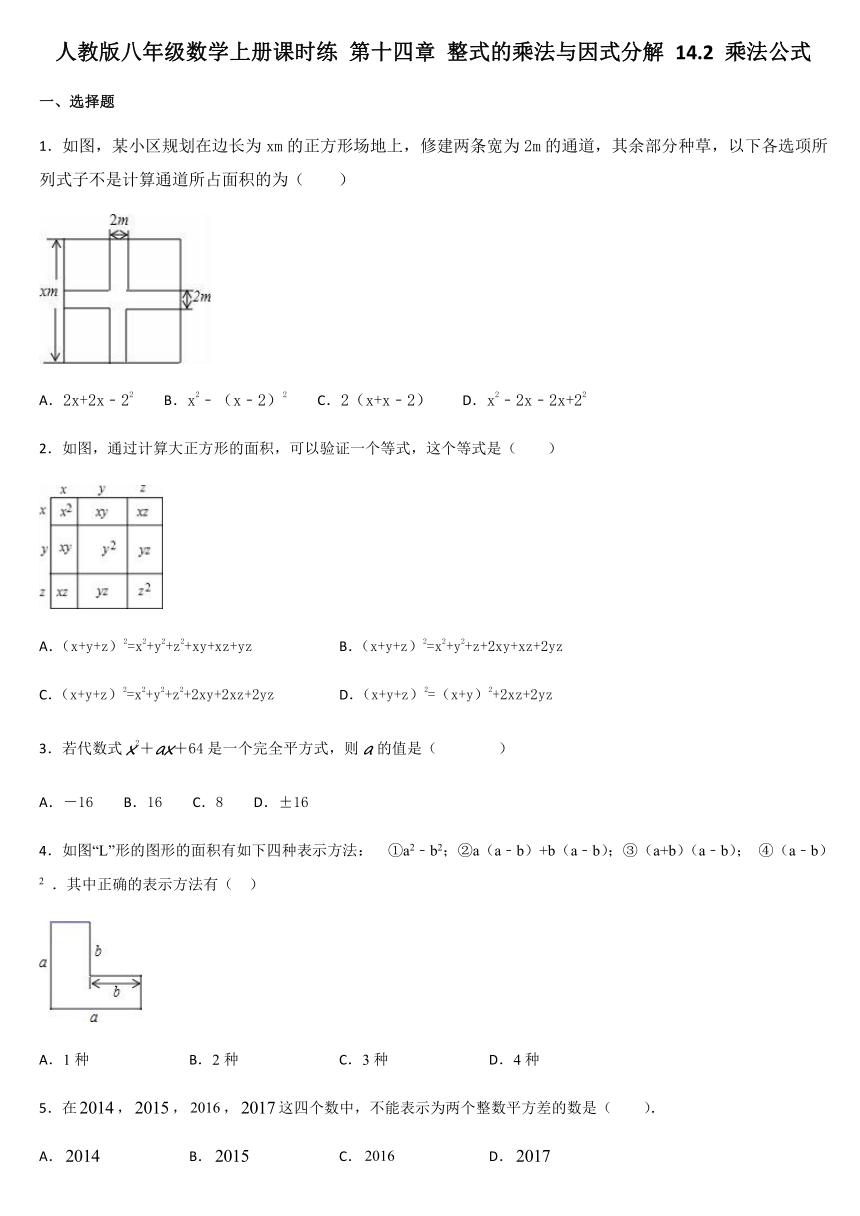 | |
| 格式 | docx | ||
| 文件大小 | 577.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 17:51:10 | ||
图片预览



文档简介
人教版八年级数学上册课时练
第十四章
整式的乘法与因式分解
14.2
乘法公式
一、选择题
1.如图,某小区规划在边长为xm的正方形场地上,修建两条宽为2m的通道,其余部分种草,以下各选项所列式子不是计算通道所占面积的为( )
A.2x+2x﹣22
B.x2﹣(x﹣2)2
C.2(x+x﹣2)
D.x2﹣2x﹣2x+22
2.如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
A.(x+y+z)2=x2+y2+z2+xy+xz+yz
B.(x+y+z)2=x2+y2+z+2xy+xz+2yz
C.(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
D.(x+y+z)2=(x+y)2+2xz+2yz
3.若代数式x2+ax+64是一个完全平方式,则a的值是(
)
A.-16
B.16
C.8
D.±16
4.如图“L”形的图形的面积有如下四种表示方法:
①a2﹣b2;②a(a﹣b)+b(a﹣b);③(a+b)(a﹣b);
④(a﹣b)2
.其中正确的表示方法有(??
)
A.1种
B.2种
C.3种
D.4种
5.在,,,这四个数中,不能表示为两个整数平方差的数是(
).
A.
B.
C.
D.
6.…+1
的个位数字为(
)
A.2
B.4
C.6
D.8
7.若(x+y)2=9,(x-y)2=5,则xy的值为(
)
A.-1
B.1
C.-4
D.4
8.已知,,,则的值为
A.0
B.1
C.2
D.3
9.已知是一个有理数的平方,则n不能取以下各数中的哪一个
A.30
B.32
C.
D.9
10.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是(
)
A.80
B.40
C.20
D.10
二、填空题
11.现有如图①的小长方形纸片若干块,已知小长方形的长为a(cm),宽为b(cm),用3个如图②的完全相同的图形和8个如图①的小长方形,拼成如图③的大长方形,则图③中阴影部分面积与整个图形的面积之比为________.
12.若则________________.
13.已知,求的值为____.
14.若,则__________.
15.计算:
_______________.
三、解答题
16.阅读下列材料:
数学中枚举法是一种重要归纳法也称为列举法、穷举法,是暴力策略的具体体现,又称为蛮力法.用枚举法解题时应该注意:
1、常常需要将对象进行恰当分类.
2、使其确定范围尽可能最小,逐个试验寻求答案.
正整数的末尾为5称为“威武数”,那么的平方数为称为“平武数”.
例:
,
,
,
,
,
……
由以上的枚举可以归纳得到的“平武数”特点是:
①“平武数”的末两位数字是25;
②去掉末两位数字25后,剩下部分组成的数字等于“平武数”去掉个位数字5后剩部分组成的数字与比此数大1的数之积.(如例中的括号内容)
(1)根据以上特点我们能够很快的推出一个四位数的“平武数”一共有___________个.
(2)同学们用学过的完全平方公式求证:当“威武数”为任意二位数时“平武数”都满足以上特点.
(3)已知“平武数”的首位数是2且小于六位,又满足的各位数字之和与的各位数字之和相等,求出“平武数”的值.
17.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中的阴影部分的正方形的边长等于______
(2)观察图2你能写出下列三个代数式(m+n)2,(m-n)2,mn之间的等量关系
_____
(3)运用你所得到的公式,计算若mn=-2,m-n=4,求①
(m+n)2的值.②
m4+n4的值.
(4)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
(5)试画出一个几何图形,使它的面积等于3m2+4mn+n2
18.下图中每个小正方形的边长均为1,观察图中正方形的面积与等式关系,完成后面的问题:
(1)根据你发现的规律,在图的后面的横线上填上所对应的等式,并证明等式成立;
(2)利用上述规律,求;
(3)利用(2)的结论求的值.
19.[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、、之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若,,则=
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知,,利用上面的规律求的值.
20.我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到.请回答下列问题:
(1)写出图2中所表示的数学等式是
;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有,的式子表示)
;
(3)通过上述的等量关系,我们可知:
当两个正数的和一定时,它们的差的绝对值越小,则积越
(填“
大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越
(填“
大”或“小”).
21.先阅读材料,再解答问题:
例:已知x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,则x=(a+1)(a-2)=,y
=a(a-1)=,
∵x-y==-2,
∴x<y.
问题:已知x=20182018×20182022-20182019×20182021,y=20182019×20182023-20182020×20182022,试比较x、y的大小.
22.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
(1)请你用两种不同的方法求图2中阴影部分的面积?
①
②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
23.在学习完全平方公式这一节课中,北师大版《数学》七年级下册教材中利用一个图形(如图1),通过不同的方法计算图形的面积来验证完全平方公式:.
(1)根据上面的原理,利用图2可以验证的等式为:
;利用图3可以验证的等式为:
;
(2)利用(1)中所得结论,解决下面的问题:求的值;
(3)如图,有三类长方形(或正方形)卡片(),其中甲同学持有类卡片各一张,乙同学持有类卡片各一张,丙同学持有类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是
.(直接写出结果)
【参考答案】
1.D
2.C
3.D
4.C
5.A
6.C
7.B
8.D
9.B
10.C
11.1:6
12.
13.47
14.
15.1
16.(1)7;(2)略;(3)2025或21025
17.(1);(2);(3)①②;(4);(5)略.
18.(1),证明略;(2);(3)4905.
19.(1)
a-b;(2);
;
(3);(4)
14;(5)
(a+b)3=a3+b3+3a2b+3ab2;(6)
9.
20.(1);(2);
(3)大
小
21.
22.(1)①(m﹣n)2;②(m+n)2﹣4mn;(2)(m﹣n)2=(m+n)2﹣4mn;(3)25.
23.(1);;(2)29;(3).
第十四章
整式的乘法与因式分解
14.2
乘法公式
一、选择题
1.如图,某小区规划在边长为xm的正方形场地上,修建两条宽为2m的通道,其余部分种草,以下各选项所列式子不是计算通道所占面积的为( )
A.2x+2x﹣22
B.x2﹣(x﹣2)2
C.2(x+x﹣2)
D.x2﹣2x﹣2x+22
2.如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
A.(x+y+z)2=x2+y2+z2+xy+xz+yz
B.(x+y+z)2=x2+y2+z+2xy+xz+2yz
C.(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
D.(x+y+z)2=(x+y)2+2xz+2yz
3.若代数式x2+ax+64是一个完全平方式,则a的值是(
)
A.-16
B.16
C.8
D.±16
4.如图“L”形的图形的面积有如下四种表示方法:
①a2﹣b2;②a(a﹣b)+b(a﹣b);③(a+b)(a﹣b);
④(a﹣b)2
.其中正确的表示方法有(??
)
A.1种
B.2种
C.3种
D.4种
5.在,,,这四个数中,不能表示为两个整数平方差的数是(
).
A.
B.
C.
D.
6.…+1
的个位数字为(
)
A.2
B.4
C.6
D.8
7.若(x+y)2=9,(x-y)2=5,则xy的值为(
)
A.-1
B.1
C.-4
D.4
8.已知,,,则的值为
A.0
B.1
C.2
D.3
9.已知是一个有理数的平方,则n不能取以下各数中的哪一个
A.30
B.32
C.
D.9
10.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是(
)
A.80
B.40
C.20
D.10
二、填空题
11.现有如图①的小长方形纸片若干块,已知小长方形的长为a(cm),宽为b(cm),用3个如图②的完全相同的图形和8个如图①的小长方形,拼成如图③的大长方形,则图③中阴影部分面积与整个图形的面积之比为________.
12.若则________________.
13.已知,求的值为____.
14.若,则__________.
15.计算:
_______________.
三、解答题
16.阅读下列材料:
数学中枚举法是一种重要归纳法也称为列举法、穷举法,是暴力策略的具体体现,又称为蛮力法.用枚举法解题时应该注意:
1、常常需要将对象进行恰当分类.
2、使其确定范围尽可能最小,逐个试验寻求答案.
正整数的末尾为5称为“威武数”,那么的平方数为称为“平武数”.
例:
,
,
,
,
,
……
由以上的枚举可以归纳得到的“平武数”特点是:
①“平武数”的末两位数字是25;
②去掉末两位数字25后,剩下部分组成的数字等于“平武数”去掉个位数字5后剩部分组成的数字与比此数大1的数之积.(如例中的括号内容)
(1)根据以上特点我们能够很快的推出一个四位数的“平武数”一共有___________个.
(2)同学们用学过的完全平方公式求证:当“威武数”为任意二位数时“平武数”都满足以上特点.
(3)已知“平武数”的首位数是2且小于六位,又满足的各位数字之和与的各位数字之和相等,求出“平武数”的值.
17.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中的阴影部分的正方形的边长等于______
(2)观察图2你能写出下列三个代数式(m+n)2,(m-n)2,mn之间的等量关系
_____
(3)运用你所得到的公式,计算若mn=-2,m-n=4,求①
(m+n)2的值.②
m4+n4的值.
(4)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
(5)试画出一个几何图形,使它的面积等于3m2+4mn+n2
18.下图中每个小正方形的边长均为1,观察图中正方形的面积与等式关系,完成后面的问题:
(1)根据你发现的规律,在图的后面的横线上填上所对应的等式,并证明等式成立;
(2)利用上述规律,求;
(3)利用(2)的结论求的值.
19.[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出(a+b)2、、之间的等量关系是____________________________________________;
(4)根据(3)中的等量关系解决如下问题:若,,则=
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知,,利用上面的规律求的值.
20.我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到.请回答下列问题:
(1)写出图2中所表示的数学等式是
;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有,的式子表示)
;
(3)通过上述的等量关系,我们可知:
当两个正数的和一定时,它们的差的绝对值越小,则积越
(填“
大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越
(填“
大”或“小”).
21.先阅读材料,再解答问题:
例:已知x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,则x=(a+1)(a-2)=,y
=a(a-1)=,
∵x-y==-2,
∴x<y.
问题:已知x=20182018×20182022-20182019×20182021,y=20182019×20182023-20182020×20182022,试比较x、y的大小.
22.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
(1)请你用两种不同的方法求图2中阴影部分的面积?
①
②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
23.在学习完全平方公式这一节课中,北师大版《数学》七年级下册教材中利用一个图形(如图1),通过不同的方法计算图形的面积来验证完全平方公式:.
(1)根据上面的原理,利用图2可以验证的等式为:
;利用图3可以验证的等式为:
;
(2)利用(1)中所得结论,解决下面的问题:求的值;
(3)如图,有三类长方形(或正方形)卡片(),其中甲同学持有类卡片各一张,乙同学持有类卡片各一张,丙同学持有类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是
.(直接写出结果)
【参考答案】
1.D
2.C
3.D
4.C
5.A
6.C
7.B
8.D
9.B
10.C
11.1:6
12.
13.47
14.
15.1
16.(1)7;(2)略;(3)2025或21025
17.(1);(2);(3)①②;(4);(5)略.
18.(1),证明略;(2);(3)4905.
19.(1)
a-b;(2);
;
(3);(4)
14;(5)
(a+b)3=a3+b3+3a2b+3ab2;(6)
9.
20.(1);(2);
(3)大
小
21.
22.(1)①(m﹣n)2;②(m+n)2﹣4mn;(2)(m﹣n)2=(m+n)2﹣4mn;(3)25.
23.(1);;(2)29;(3).
