北师大版八年级数学上册第三章 位置与坐标综合测评(Word版 含答案)
文档属性
| 名称 | 北师大版八年级数学上册第三章 位置与坐标综合测评(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 639.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 19:24:19 | ||
图片预览


文档简介
第三章 位置与坐标综合测评
一、选择题(每小题3分,共30分)
1.根据下列表述,能确定位置的是( )
A. 广州白云区以北 B. 万达广场3楼
C. 博罗中学北偏东35° D. 东经120°,北纬30°
2.在平面直角坐标系中,若点A(-m,n)在第四象限,则点B(1-n,m)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 在平面直角坐标系中,下列各点在y轴上的点是 (???? ? )
A. ( 2,0 )?? ???? ? B. ( -2,3 )?? ????? C. (0,3)??????? ? D. ( 1,-3 )
4.小明和妈妈在家门口打车出行,借助某打车软件,他看到了当时附近的出租车分布情况.若以他现在的位置为原点,正东、正北分别为x轴、y轴的正方向,图1中点A的坐标为(1,0),那么离他最近的出租车所在位置的坐标大约是( )
A.(3.2,1.3) B.(-1.9,0.7) C.(0.7,-1.9) D.(3.8,-2.6)
图1
5. 已知点A(2,-1)和点B(m-1,3),如果直线AB∥y轴,那么m的值为( )
A. 1 B. -4 C. -1 D. 3
6.点P(m,-2)与点P1(-4,n)关于x轴对称,则m,n的值分别为( )
A. 4,-2 B. -4,2 C. -4,-2 D. 4,2
7. 有下列说法:①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;
④点(-2,-6)在第三象限内.
其中正确的有( )
0个 B. 1个
C. 2个 D. 3个
8. 已知直角坐标系中点P到y轴的距离为5,且点P到x轴的距离为3,则这样的点P的个数是( )
A.1 B.2 C.3 D.4
9. 图2为晓莉使用微信与晓红的对话记录.根据图中两个人的对话记录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
A.向北直走700米,再向西直走100米 B.向北直走100米,再向东直走700米
C.向北直走300米,再向西直走400米 D.向北直走400米,再向东直走300米
图2 图3
10. 如图3,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的格点上,在第四象限内的格点
上找点C,使△ABC的面积为3,则这样的点C共有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(本大题共6小题,每小题4分,共24分.请你把答案填在横线上方)
11. 如果用(7,3)表示七年级三班,则(9,6)表示________.
12. 在平面直角坐标系中,点P(-2,1)关于y轴对称的点P的坐标是________.
13. 已知点P(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,则a= .
14. 图4是北京市地铁部分线路示意图.若分别以正东、正北方向为x轴,y轴的正方向建立平面直角坐标系,表示西单的点的坐标为(-4,0),表示雍和宫的点的坐标为(4,6),则表示南锣鼓巷的点的坐标是 .?
图4 图5
15.在平面直角坐标系中,一个点的横、纵坐标都是整数,并且它们的乘积是4,满足条件的点共有 个.
16.如图5,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次运动到点(-2,0),第3次运动到点(-3,2),…… 按这样的运动规律,经过第2020次运动后,动点P的坐标是_______.
三、解答题(共52分)
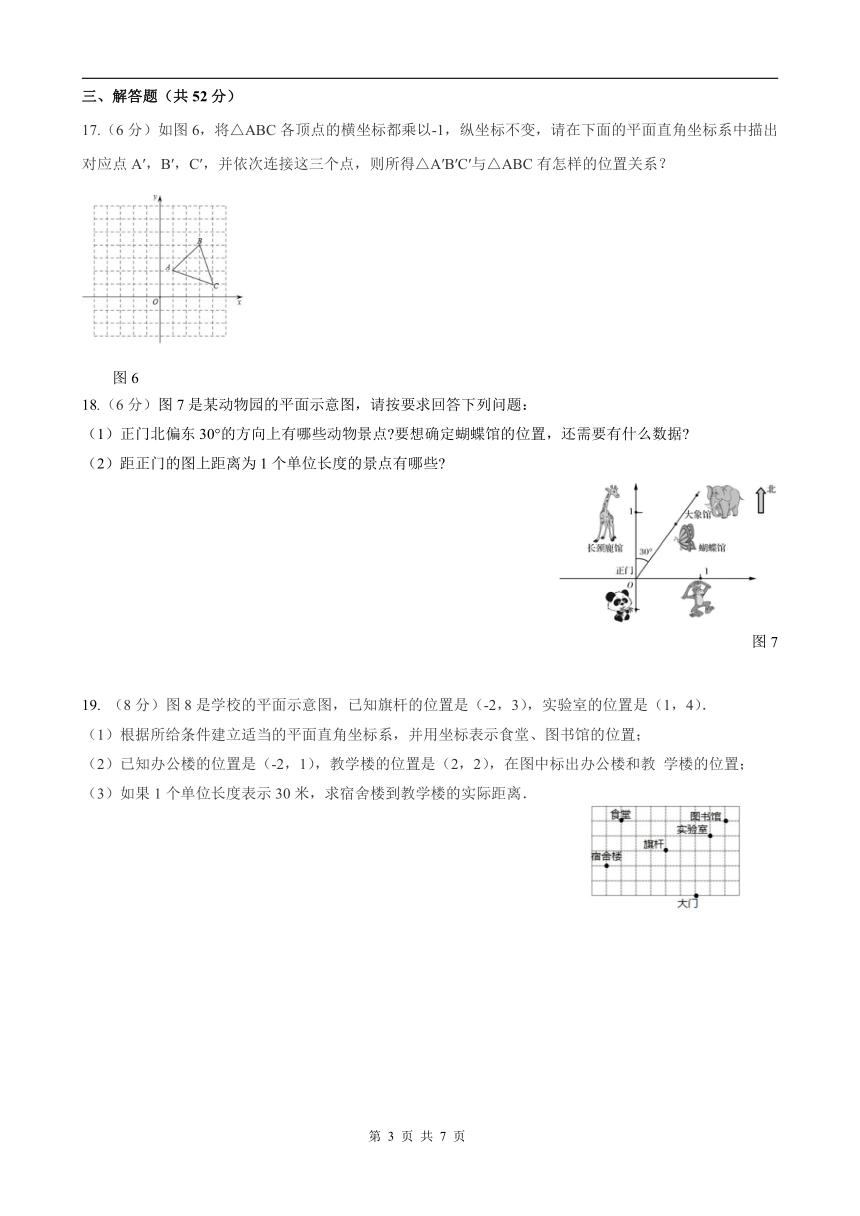
17.(6分)如图6,将△ABC各顶点的横坐标都乘以-1,纵坐标不变,请在下面的平面直角坐标系中描出对应点A′,B′,C′,并依次连接这三个点,则所得△A′B′C′与△ABC有怎样的位置关系?
图6
18.(6分)图7是某动物园的平面示意图,请按要求回答下列问题:
(1)正门北偏东30°的方向上有哪些动物景点?要想确定蝴蝶馆的位置,还需要有什么数据?
(2)距正门的图上距离为1个单位长度的景点有哪些?
图7
19. (8分)图8是学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4).
(1)根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂、图书馆的位置;
(2)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教 学楼的位置;
(3)如果1个单位长度表示30米,求宿舍楼到教学楼的实际距离.
20.(10分)如图9,平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4),求四边形ABCD的面积.
21. (10分)在平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中“+”是四则运算中的加法),例如点P(1,2)的勾股值为[P]=|1|+|2|=3.
(1)求点A(-2,4),B(,)的勾股值[A],[B];
(2)若点M在x轴的上方,其横、纵坐标均为整数,且[M]=3,请求出点M的坐标.
22.(12分)如图10,一只甲虫在5×5的方格(每个小方格的边长为1)上沿着网格线运动. 它从A处出发去看望B,C,D处的其他甲虫,规定:向上、向右走均为正,向下、向左走均为负. 如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→D( , ),C→B( , ),B → (+3,-2);
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+1,+2),(+4,-1),(-2,+3),(-1,-1),请
在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B →C→D,请计算该甲虫走过的路程.
(4)若图中另有两个格点M,N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
图10
附加题(20分,不计入总分)
23. 在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴,y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1)直接写出点B和点C的坐标:B ,C ;
(2)当点P运动时,用含t的式子表示线段AP的长;(不要求写出t的取值范围)(3)点D(2,0),连接PD,AD,在(2)的条件下是否存在这样的t值,使S△APD=S四边形ABOC,若存在,请求出t值;若不存在,请说明理由.
图11
第三章 位置与坐标综合测评
一、1.D 2.D 3.C 4.B 5.D 6.B 7.C 8.D 9.A 10.B
二、11. 九年级六班 12.(2,1) 13.-9 14.(1,3) 15.6
16. (-2020,0) 提示:动点P第1次从原点运动到点(-1,1),第2次运动到点(-2,0),第3次运动到点(-3,2),第4次运动到点(-4,0),第5次接着运动到点(-5,1),……所以经过第2020次运动后,动点P的横坐标为-2020;纵坐标为1,0,2,0,每4个为一个循环,且2020÷4=505,所以纵坐标为0.即经过第2020次运动后,动点P的坐标是(-2020,0).
三、17.解:如图1,△A′B′C′与△ABC关于y轴对称.
图1
18. 解:(1)观察图形知,正门北偏东30°的方向上的有蝴蝶馆、大象馆.要想确定蝴蝶馆的位置,还需知道蝴蝶
馆与正门的距离.
(2)距正门的图上距离为1个单位长度的景点有长颈鹿馆和猴园.
19. 解:(1)建立平面直角坐标系如图2所示,食堂(-5,5),图书馆(2,5).
图2
(2)如图2所示,办公楼和教学楼的位置即为所求.
(3)由坐标系可知宿舍楼到教学楼的距离是8个单位长度,所以宿舍楼到教学楼的实际距离为:8×30=
240(米).
20. 解:如图3,作CE⊥x轴于点E,DF⊥x轴于点F.
图3
则S△ADF=×(2-1)×4=2,S梯形DCEF=×(3+4)×(3-2)=3.5,S△BCE=×(5-3)×3=3.
所以S四边形ABCD=2+3.5+3=8.5.
答:四边形ABCD的面积是8.5.
21. 解:(1)由题意,[A]=|-2|+|4|=2+4=6,[B]=||+||==2.
(2)因为点M在x轴的上方,其横、纵坐标均为整数,且[M]=3,所以x=±1,y=2,或x=±2,y=1,x=0,y=3.
所以点M的坐标为(-1,2),(1,2),(-2,1),(2,1)或(0,3).
22. 解:(1)+4 +2 -2 0 D
(2)点P的位置如图4所示.
图4
(3)AB记为(1,4),BC记为(2,0),CD记为(1,-2),则该甲虫走过的路程为1+4+2+1+2=10.
(4)由MA(3-a,b-4),MN(5-a,b-2),所以5-a-(3-a)=2,b-2-(b-4)=2.
所以点A向右走2格,向上走2格到N,所以NA记为(-2,-2).
23. 解:(1)(0,6) (8,0)
(2)由题意可得AB=8,AC=6.当点P在线段BA上时, AP=8-2t;
当点P在线段AC上时,AP=2t-8.
(3)如图5,当点P在线段BA上时,AB÷2=4,所以t<4.
设点D到AP的距离为h,则h=AC.
因为S△APD=AP?h=AP?AC,S四边形ABOC=AB?AC,所以?(8-2t)×6=×8×6,解得t=3<4;
图5 图6
如图6,当点P在线段AC上时,4<t<,即4<t<7.
因为S△APD=AP?CD,CD=8-2=6,S四边形ABOC=AB?AC,所以?(2t-8)×6=×8×6,解得t=5<7.
综上所述,当t为3秒或5秒时,S△APD=S四边形ABOC.
第 1 页 共 4 页
一、选择题(每小题3分,共30分)
1.根据下列表述,能确定位置的是( )
A. 广州白云区以北 B. 万达广场3楼
C. 博罗中学北偏东35° D. 东经120°,北纬30°
2.在平面直角坐标系中,若点A(-m,n)在第四象限,则点B(1-n,m)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 在平面直角坐标系中,下列各点在y轴上的点是 (???? ? )
A. ( 2,0 )?? ???? ? B. ( -2,3 )?? ????? C. (0,3)??????? ? D. ( 1,-3 )
4.小明和妈妈在家门口打车出行,借助某打车软件,他看到了当时附近的出租车分布情况.若以他现在的位置为原点,正东、正北分别为x轴、y轴的正方向,图1中点A的坐标为(1,0),那么离他最近的出租车所在位置的坐标大约是( )
A.(3.2,1.3) B.(-1.9,0.7) C.(0.7,-1.9) D.(3.8,-2.6)
图1
5. 已知点A(2,-1)和点B(m-1,3),如果直线AB∥y轴,那么m的值为( )
A. 1 B. -4 C. -1 D. 3
6.点P(m,-2)与点P1(-4,n)关于x轴对称,则m,n的值分别为( )
A. 4,-2 B. -4,2 C. -4,-2 D. 4,2
7. 有下列说法:①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;
④点(-2,-6)在第三象限内.
其中正确的有( )
0个 B. 1个
C. 2个 D. 3个
8. 已知直角坐标系中点P到y轴的距离为5,且点P到x轴的距离为3,则这样的点P的个数是( )
A.1 B.2 C.3 D.4
9. 图2为晓莉使用微信与晓红的对话记录.根据图中两个人的对话记录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
A.向北直走700米,再向西直走100米 B.向北直走100米,再向东直走700米
C.向北直走300米,再向西直走400米 D.向北直走400米,再向东直走300米
图2 图3
10. 如图3,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的格点上,在第四象限内的格点
上找点C,使△ABC的面积为3,则这样的点C共有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(本大题共6小题,每小题4分,共24分.请你把答案填在横线上方)
11. 如果用(7,3)表示七年级三班,则(9,6)表示________.
12. 在平面直角坐标系中,点P(-2,1)关于y轴对称的点P的坐标是________.
13. 已知点P(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,则a= .
14. 图4是北京市地铁部分线路示意图.若分别以正东、正北方向为x轴,y轴的正方向建立平面直角坐标系,表示西单的点的坐标为(-4,0),表示雍和宫的点的坐标为(4,6),则表示南锣鼓巷的点的坐标是 .?
图4 图5
15.在平面直角坐标系中,一个点的横、纵坐标都是整数,并且它们的乘积是4,满足条件的点共有 个.
16.如图5,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次运动到点(-2,0),第3次运动到点(-3,2),…… 按这样的运动规律,经过第2020次运动后,动点P的坐标是_______.
三、解答题(共52分)
17.(6分)如图6,将△ABC各顶点的横坐标都乘以-1,纵坐标不变,请在下面的平面直角坐标系中描出对应点A′,B′,C′,并依次连接这三个点,则所得△A′B′C′与△ABC有怎样的位置关系?
图6
18.(6分)图7是某动物园的平面示意图,请按要求回答下列问题:
(1)正门北偏东30°的方向上有哪些动物景点?要想确定蝴蝶馆的位置,还需要有什么数据?
(2)距正门的图上距离为1个单位长度的景点有哪些?
图7
19. (8分)图8是学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4).
(1)根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂、图书馆的位置;
(2)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教 学楼的位置;
(3)如果1个单位长度表示30米,求宿舍楼到教学楼的实际距离.
20.(10分)如图9,平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4),求四边形ABCD的面积.
21. (10分)在平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中“+”是四则运算中的加法),例如点P(1,2)的勾股值为[P]=|1|+|2|=3.
(1)求点A(-2,4),B(,)的勾股值[A],[B];
(2)若点M在x轴的上方,其横、纵坐标均为整数,且[M]=3,请求出点M的坐标.
22.(12分)如图10,一只甲虫在5×5的方格(每个小方格的边长为1)上沿着网格线运动. 它从A处出发去看望B,C,D处的其他甲虫,规定:向上、向右走均为正,向下、向左走均为负. 如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→D( , ),C→B( , ),B → (+3,-2);
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+1,+2),(+4,-1),(-2,+3),(-1,-1),请
在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B →C→D,请计算该甲虫走过的路程.
(4)若图中另有两个格点M,N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
图10
附加题(20分,不计入总分)
23. 在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴,y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1)直接写出点B和点C的坐标:B ,C ;
(2)当点P运动时,用含t的式子表示线段AP的长;(不要求写出t的取值范围)(3)点D(2,0),连接PD,AD,在(2)的条件下是否存在这样的t值,使S△APD=S四边形ABOC,若存在,请求出t值;若不存在,请说明理由.
图11
第三章 位置与坐标综合测评
一、1.D 2.D 3.C 4.B 5.D 6.B 7.C 8.D 9.A 10.B
二、11. 九年级六班 12.(2,1) 13.-9 14.(1,3) 15.6
16. (-2020,0) 提示:动点P第1次从原点运动到点(-1,1),第2次运动到点(-2,0),第3次运动到点(-3,2),第4次运动到点(-4,0),第5次接着运动到点(-5,1),……所以经过第2020次运动后,动点P的横坐标为-2020;纵坐标为1,0,2,0,每4个为一个循环,且2020÷4=505,所以纵坐标为0.即经过第2020次运动后,动点P的坐标是(-2020,0).
三、17.解:如图1,△A′B′C′与△ABC关于y轴对称.
图1
18. 解:(1)观察图形知,正门北偏东30°的方向上的有蝴蝶馆、大象馆.要想确定蝴蝶馆的位置,还需知道蝴蝶
馆与正门的距离.
(2)距正门的图上距离为1个单位长度的景点有长颈鹿馆和猴园.
19. 解:(1)建立平面直角坐标系如图2所示,食堂(-5,5),图书馆(2,5).
图2
(2)如图2所示,办公楼和教学楼的位置即为所求.
(3)由坐标系可知宿舍楼到教学楼的距离是8个单位长度,所以宿舍楼到教学楼的实际距离为:8×30=
240(米).
20. 解:如图3,作CE⊥x轴于点E,DF⊥x轴于点F.
图3
则S△ADF=×(2-1)×4=2,S梯形DCEF=×(3+4)×(3-2)=3.5,S△BCE=×(5-3)×3=3.
所以S四边形ABCD=2+3.5+3=8.5.
答:四边形ABCD的面积是8.5.
21. 解:(1)由题意,[A]=|-2|+|4|=2+4=6,[B]=||+||==2.
(2)因为点M在x轴的上方,其横、纵坐标均为整数,且[M]=3,所以x=±1,y=2,或x=±2,y=1,x=0,y=3.
所以点M的坐标为(-1,2),(1,2),(-2,1),(2,1)或(0,3).
22. 解:(1)+4 +2 -2 0 D
(2)点P的位置如图4所示.
图4
(3)AB记为(1,4),BC记为(2,0),CD记为(1,-2),则该甲虫走过的路程为1+4+2+1+2=10.
(4)由MA(3-a,b-4),MN(5-a,b-2),所以5-a-(3-a)=2,b-2-(b-4)=2.
所以点A向右走2格,向上走2格到N,所以NA记为(-2,-2).
23. 解:(1)(0,6) (8,0)
(2)由题意可得AB=8,AC=6.当点P在线段BA上时, AP=8-2t;
当点P在线段AC上时,AP=2t-8.
(3)如图5,当点P在线段BA上时,AB÷2=4,所以t<4.
设点D到AP的距离为h,则h=AC.
因为S△APD=AP?h=AP?AC,S四边形ABOC=AB?AC,所以?(8-2t)×6=×8×6,解得t=3<4;
图5 图6
如图6,当点P在线段AC上时,4<t<,即4<t<7.
因为S△APD=AP?CD,CD=8-2=6,S四边形ABOC=AB?AC,所以?(2t-8)×6=×8×6,解得t=5<7.
综上所述,当t为3秒或5秒时,S△APD=S四边形ABOC.
第 1 页 共 4 页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
