青岛版九年级数学上册课件:4.6《一元二次方程根与系数的关系》(共16张)
文档属性
| 名称 | 青岛版九年级数学上册课件:4.6《一元二次方程根与系数的关系》(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 199.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 00:00:00 | ||
图片预览




文档简介
4.6 一元二次方程根与系数的关系
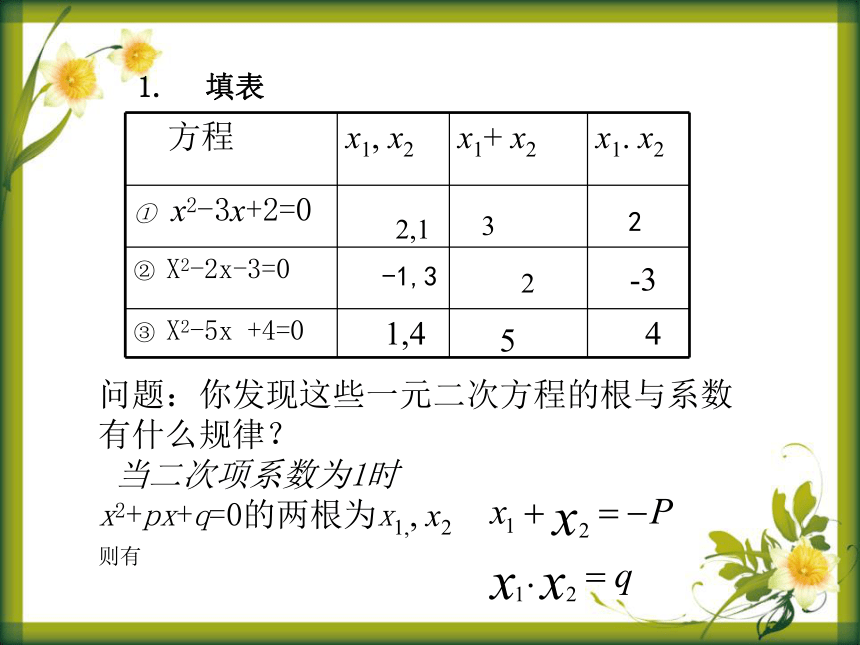
1.???? 填表
方程
x1, x2
x1+ x2
x1. x2
① x2-3x+2=0
② X2-2x-3=0
③ X2-5x +4=0
问题:你发现这些一元二次方程的根与系数
有什么规律?
当二次项系数为1时
x2+px+q=0的两根为x1,, x2
则有
2,1
3
2
-1,3
2
-3
1,4
5
4
方程
1
-2
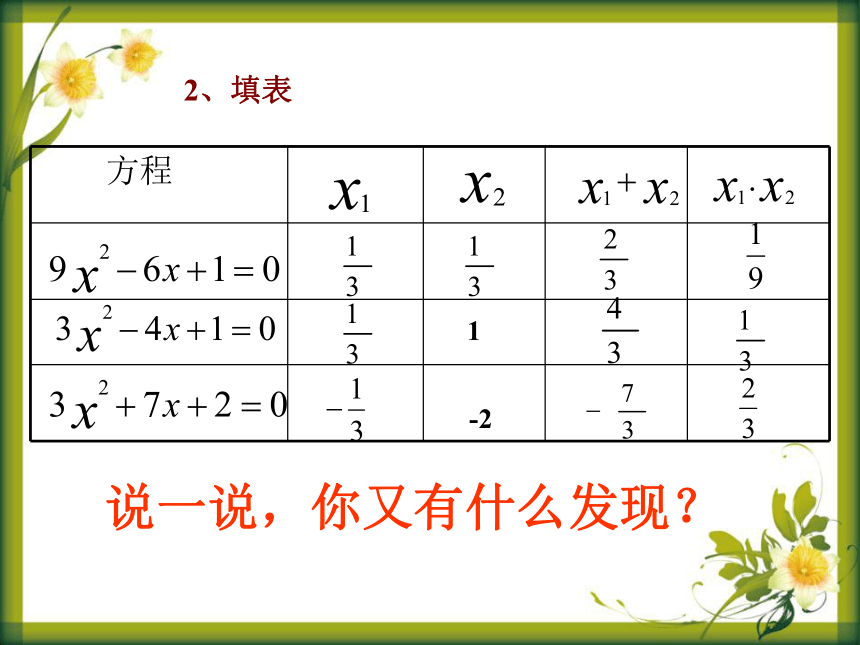
2、填表
说一说,你又有什么发现?
猜想:
如果一元二次方程
ax2+bx+c=0(a、b、c是常数且a=0 )的两根为x1、x2,则
x1.x2与系数a,b,c 的关系。
任意的一元二次方程
ax2+bx+c=0(a≠0 )的x1+x2, x1.x2与系数a,b,c 的关系是: x1+x2=-—
x1.x2= —
a
b
a
c
一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.
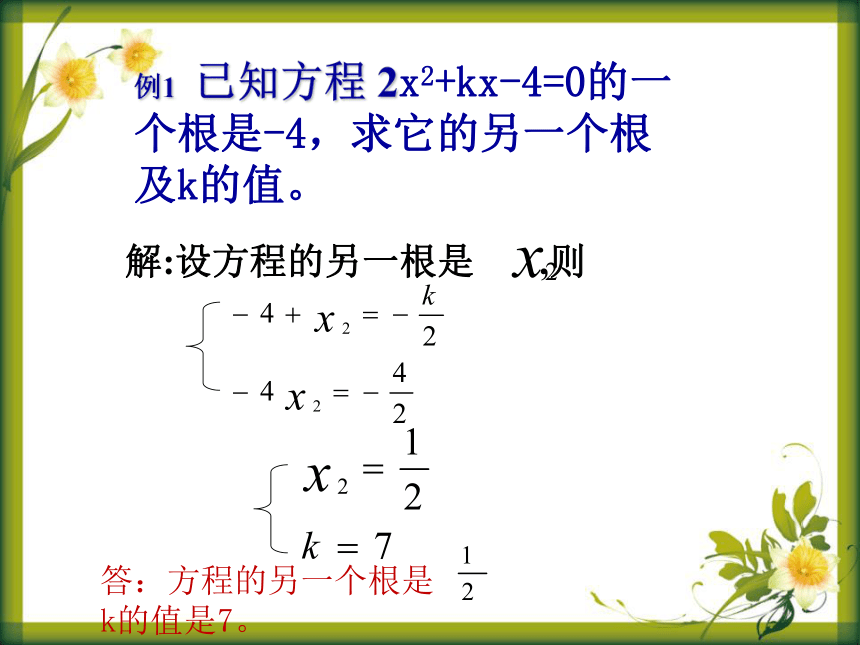
例1 已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值。
答:方程的另一个根是 k的值是7。
解:设方程的另一根是 ,则
(1)x2-3x+1=0
(2)3x2-2x=2
(3)2x2+3x=0
(4)3x2=1
1.下列方程两根的和与两根的积各是多少?(不解方程)
自主练习 灵活运用
自主练习 灵活运用
2、设x1.x2是方程2x2+4x-3=0的两个根,利用根与系数的关系,求下列各式的值。
(1)( x1+1)(x2+1)(2)— + —
x1
x2
x1
x2
一元二次方程根与系数的关系?
例题2:
(1)若关于x的方程2x2+5x+n=0的一个根是-2,求它的另一个根及n的值。
(2)若关于x的方程x2+kx-6=0的一个根是-2,求它的另一个根及k的值。
1、一元二次方程的一般形式 。
ax2+bx+c=0 (a≠0)
(1)a≠0
(2)△≥0
2、若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1 、x2,
则x1+x2= ,x1x2= 。
3、用根与系数关系解题的条件是 。
一、知识要点:
二、典型例题
例题1:已知方程 x2=2x+1的两根为x1,x2,
不解方程,求下列各式的值。
(1)(x1-x2)2 (2)x13x2+x1x23
(3)
3、已知:如图,直角梯形ABCD中,AB∥CD,
AD⊥DC,AD=10cm,
以AD 为直径的⊙O切另
一腰于E,以AB、CD为
根的方程是X2-12X+m=0,
求m的值。
A
B
C
D
O
E
提高练习
例题3:
设x1,x2是方程2x2-3x+m=0的两个根,
且8x1-2x2=7,求m的值。
例题4:
已知关于x的一元二次方程x2+(2k-1)x+k2=0
有两个不相等的实数根,且方程的两根之和比两根之积7,求k的值。
例题6:已知二次函数y=x2-mx-4
(1)求证:该函数的图象一定与x轴有两个不同的交点。
(2)设该函数的图象与x轴的交点坐标为(x1,0),(x2,0)
且有 求m的值,并求出该函数图象的
顶点坐标。
三、延伸与拓展
1.???? 填表
方程
x1, x2
x1+ x2
x1. x2
① x2-3x+2=0
② X2-2x-3=0
③ X2-5x +4=0
问题:你发现这些一元二次方程的根与系数
有什么规律?
当二次项系数为1时
x2+px+q=0的两根为x1,, x2
则有
2,1
3
2
-1,3
2
-3
1,4
5
4
方程
1
-2
2、填表
说一说,你又有什么发现?
猜想:
如果一元二次方程
ax2+bx+c=0(a、b、c是常数且a=0 )的两根为x1、x2,则
x1.x2与系数a,b,c 的关系。
任意的一元二次方程
ax2+bx+c=0(a≠0 )的x1+x2, x1.x2与系数a,b,c 的关系是: x1+x2=-—
x1.x2= —
a
b
a
c
一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.
例1 已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值。
答:方程的另一个根是 k的值是7。
解:设方程的另一根是 ,则
(1)x2-3x+1=0
(2)3x2-2x=2
(3)2x2+3x=0
(4)3x2=1
1.下列方程两根的和与两根的积各是多少?(不解方程)
自主练习 灵活运用
自主练习 灵活运用
2、设x1.x2是方程2x2+4x-3=0的两个根,利用根与系数的关系,求下列各式的值。
(1)( x1+1)(x2+1)(2)— + —
x1
x2
x1
x2
一元二次方程根与系数的关系?
例题2:
(1)若关于x的方程2x2+5x+n=0的一个根是-2,求它的另一个根及n的值。
(2)若关于x的方程x2+kx-6=0的一个根是-2,求它的另一个根及k的值。
1、一元二次方程的一般形式 。
ax2+bx+c=0 (a≠0)
(1)a≠0
(2)△≥0
2、若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1 、x2,
则x1+x2= ,x1x2= 。
3、用根与系数关系解题的条件是 。
一、知识要点:
二、典型例题
例题1:已知方程 x2=2x+1的两根为x1,x2,
不解方程,求下列各式的值。
(1)(x1-x2)2 (2)x13x2+x1x23
(3)
3、已知:如图,直角梯形ABCD中,AB∥CD,
AD⊥DC,AD=10cm,
以AD 为直径的⊙O切另
一腰于E,以AB、CD为
根的方程是X2-12X+m=0,
求m的值。
A
B
C
D
O
E
提高练习
例题3:
设x1,x2是方程2x2-3x+m=0的两个根,
且8x1-2x2=7,求m的值。
例题4:
已知关于x的一元二次方程x2+(2k-1)x+k2=0
有两个不相等的实数根,且方程的两根之和比两根之积7,求k的值。
例题6:已知二次函数y=x2-mx-4
(1)求证:该函数的图象一定与x轴有两个不同的交点。
(2)设该函数的图象与x轴的交点坐标为(x1,0),(x2,0)
且有 求m的值,并求出该函数图象的
顶点坐标。
三、延伸与拓展
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
