苏科版数学八年级上册2.5等腰三角形的性质与判断专题培优训练卷(Word版 含解析)
文档属性
| 名称 | 苏科版数学八年级上册2.5等腰三角形的性质与判断专题培优训练卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 21:46:55 | ||
图片预览



文档简介
2020-2021学年度苏科版八年级上学期数学2.5等腰三角形的性质与判断专题培优训练卷
一、选择题
1、如图,在,点在上,下列四个命题正确的有(
)
①若,则
②若,,则,
③若,,则,
④若,,则,
A.1个
B.
2个
C.
3个
D.
4个
(1)
(2)
(3)
(5)
2、如图所示,中,,是上一点,于点,若,
则的度数是
A.
B.
C.
D.
3、如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是(
)
A.60°
B.70°
C.80°
D.不确定
4、等腰三角形一腰上的高与另一腰所成的夹角为45°,则顶角的度数为(
)
A.
45°或135°
B.45°
C.135°
D.90°
5、如图,在中,和的平分线交于点,过点作,交于,交于,若,,则线段的长为
A.5
B.6
C.7
D.8
6、将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是(
)
A.
4个
B.
3个
C.
2个
D.
1个
(6)
(7)
(8)
(9)
7、如图,在中,,、两点分别在、上,是的平分线,,若,,则的周长是
A.
B.
C.
D.
8、如图,在中,,,是的平分线.若在边上截取,连接,则图中的等腰三角形共有(
)
A.
2个
B.
3个
C.
4个
D.
5个
9、如图,中,,垂直平分,,,则的度数为
A.
B.
C.
D.
10、在中,与相邻的外角是,要使为等腰三角形,则的度数是
A.
B.
C.或
D.或或
二、填空题
11、已知一个等腰三角形两边长分别为5,6,则它的周长为_________
12、等腰三角形的一个角是70°,则它的顶角的度数是
.
13、如图,A、B、C、D、E、F、G都在∠O的边上,OA=AB=BC=CD=DE=EF=FG,若∠EFG=30°,则∠O=________.
14、如图,在中,,点分别在上,且,,
若,则的度数为
.
(14)
(15)
(16)
(17)
15、如图,在△ABC中,OB、OC分别是∠ABC和∠ACB的角平分线,过点O作OE∥AB,OF∥AC,交边BC于点E、F,如果BC=10,那么C△OEF等于
.
16、如图,中,与的平分线交于点,过作交、于、,若的周长比的周长大,到的距离为,的面积
.
17、如图,在中,,点D,点E分别是BC,AC上一点,且,若,,则的度数为________.
18、如图,在中,,平分,,,、为垂足,则下列四个结论:(1);(2);(3)平分;(4)垂直平分.其中正确的有
(18)
(19)
(20)
19、如图,在△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,
则DE等于
.
20、如图,是等腰三角形,,,平分;点是射线上一点,如果
点满足是等腰三角形,那么的度数是
.
三、解答题
21、如图,在中,延长到点,使,连接,是的中线,是
的平分线.求证:
.
22、已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
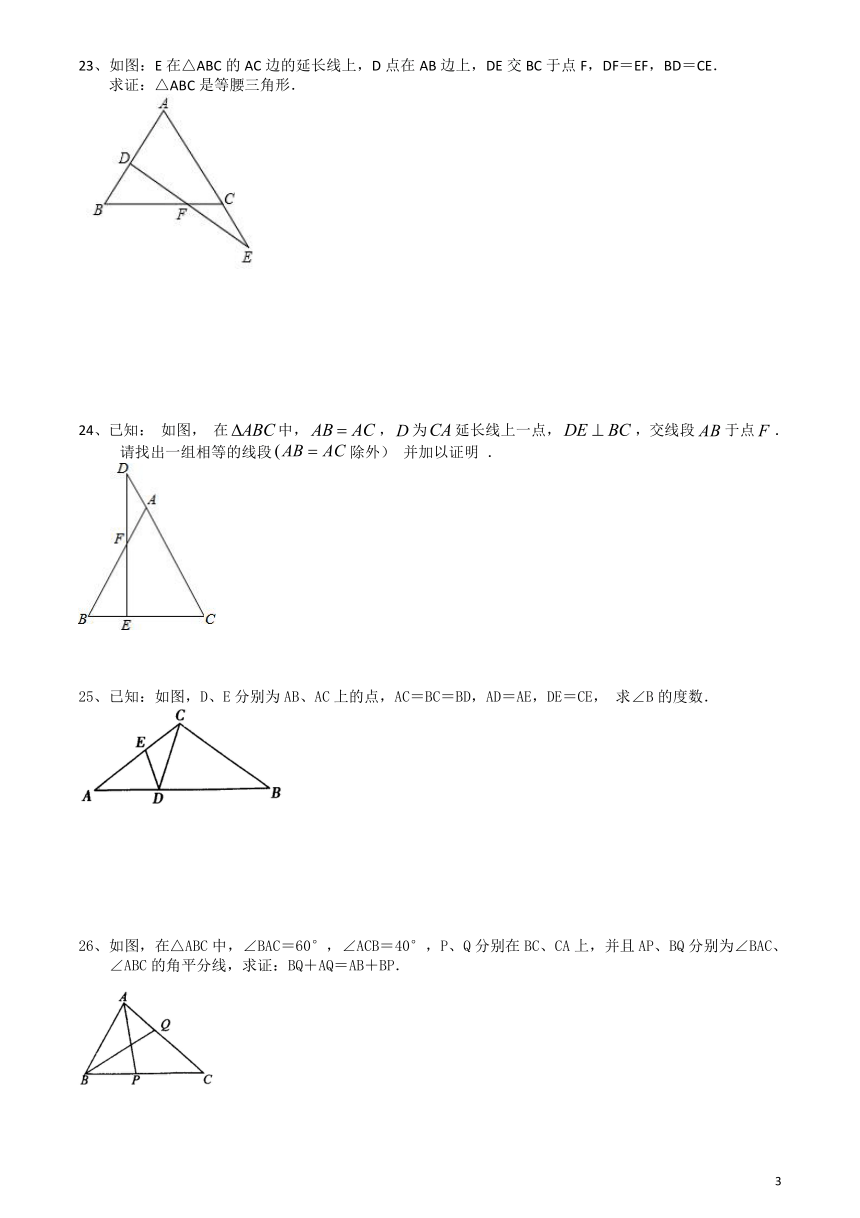
23、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.
求证:△ABC是等腰三角形.
24、已知:
如图,
在中,,为延长线上一点,,交线段于点.
请找出一组相等的线段除外)
并加以证明
.
25、已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,
求∠B的度数.
26、如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线,求证:BQ+AQ=AB+BP.
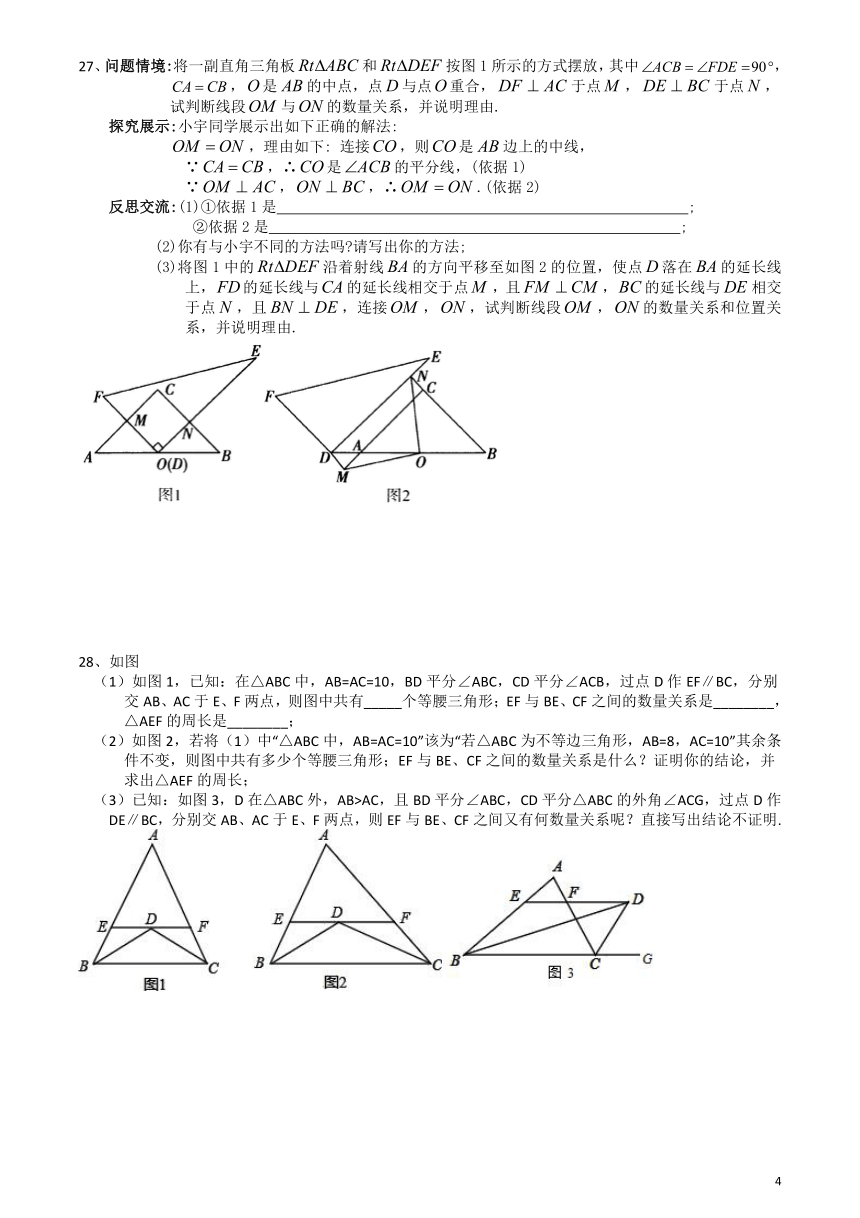
27、问题情境:将一副直角三角板和按图1所示的方式摆放,其中,
,是的中点,点与点重合,于点,于点,试判断线段与的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
,理由如下:
连接,则是边上的中线,
∵,∴是的平分线,(依据1)
∵,,∴.(依据2)
反思交流:(1)①依据1是
;
②依据2是
;
(2)你有与小宇不同的方法吗?请写出你的方法;
(3)将图1中的沿着射线的方向平移至如图2的位置,使点落在的延长线上,的延长线与的延长线相交于点,且,的延长线与相交于点,且,连接,,试判断线段,的数量关系和位置关系,并说明理由.
28、如图
(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别
交AB、AC于E、F两点,则图中共有_____个等腰三角形;EF与BE、CF之间的数量关系是________,△AEF的周长是________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有多少个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
2020-2021学年度苏科版八年级上学期数学2.5等腰三角形的性质与判断专题培优训练卷
(答案)
一、选择题
1、如图,在,点在上,下列四个命题正确的有(
D
)
①若,则
②若,,则,
③若,,则,
④若,,则,
A.1个
B.
2个
C.
3个
D.
4个
2、如图所示,中,,是上一点,于点,若,
则的度数是
A.
B.
C.
D.
【解答】解:,,,
,,.故选:.
3、如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是(
C
)
A.60°
B.70°
C.80°
D.不确定
4、等腰三角形一腰上的高与另一腰所成的夹角为45°,则顶角的度数为(
A
)
A.
45°或135°
B.45°
C.135°
D.90°
5、如图,在中,和的平分线交于点,过点作,交于,交于,若,,则线段的长为
A.5
B.6
C.7
D.8
【解析】、是、的角平分线,,,
又,,,,,
,,,故选:.
6、将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是(
B
)
A.
4个
B.
3个
C.
2个
D.
1个
7、如图,在中,,、两点分别在、上,是的平分线,,若,,则的周长是
A.
B.
C.
D.
【解析】,.
,,,,
是的平分线,.,
,的周长为,
故选:.
8、如图,在中,,,是的平分线.若在边上截取,连接,则图中的等腰三角形共有(
D
)
A.
2个
B.
3个
C.
4个
D.
5个
9、如图,中,,垂直平分,,,则的度数为
A.
B.
C.
D.
【解答】解:垂直平分,,
,是等腰直角三角形,,
又,,
,
,,,,,
.
故选:.
10、在中,与相邻的外角是,要使为等腰三角形,则的度数是
A.
B.
C.或
D.或或
【解答】解:.
当时,;
当时,,则;
当时,.
的度数为或或,
故选:.
二、填空题
11、已知一个等腰三角形两边长分别为5,6,则它的周长为___16或17
______
12、等腰三角形的一个角是70°,则它的顶角的度数是
70°或40o;
.
13、如图,A、B、C、D、E、F、G都在∠O的边上,OA=AB=BC=CD=DE=EF=FG,若∠EFG=30°,则∠O=________.
解:∵∠O=x,OA=AB=BC=CD=DE=EF=FG,
∴∠BAC=2x,∴∠CBD=3x;∴∠DCE=4x,
∴∠FDE=5x,∴∠FEG=6x,
∵EF=FG,∴∠FEG=∠FGE,
∵∠EFG=30°,∴∠FEG=6x=75°,∴x=12.5o
,
∴∠O=12.5°.故答案为:12.5°.
14、如图,在中,,点分别在上,且,,
若,则的度数为
70°
.
15、如图,在△ABC中,OB、OC分别是∠ABC和∠ACB的角平分线,过点O作OE∥AB,OF∥AC,交边BC于点E、F,如果BC=10,那么C△OEF等于
10
.
16、如图,中,与的平分线交于点,过作交、于、,若的周长比的周长大,到的距离为,的面积
.
【解析】与的平分线交于点,,,
,,,
,,,,
,,
的周长比的周长大,,
,
到的距离为,的面积是.,
故答案为:
18
.
17、如图,在中,,点D,点E分别是BC,AC上一点,且,若,,则的度数为________.
解:,,
,,,
,,
,,
18、如图,在中,,平分,,,、为垂足,则下列四个结论:(1);(2);(3)平分;(4)垂直平分.其中正确的有①②③正确
19、如图,在△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,
则DE等于
.
【解析】解:∵BI、CI分别平分∠ABC、∠ACF,∴∠ABI=∠CBI,∠ECI=∠ICF,
∵DE∥BC,∴∠DIB=∠CBI,∠EIC=∠ICF,
∴∠ABI=∠DIB,∠ECI=∠EIC,
∴DI=BD=8cm,EI=CE=5cm,∴DE=DI﹣EI=3cm.
20、如图,是等腰三角形,,,平分;点是射线上一点,如果
点满足是等腰三角形,那么的度数是 、或 .
【解答】解:当时,如图所示,
,,,
平分,,,,
当时,如图所示,
,,,
平分,,,.
当时,如图所示,
,,,
平分,,,,
故答案为:、或.
三、解答题
21、如图,在中,延长到点,使,连接,是的中线,是
的平分线.求证:
.
∵CD=CA,CF是的中线,
是的平分线,
∵CE是的平分线,,
22、已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
证明:ED⊥BC;延长ED,交BC边于H,
∵AB=AC,AE=AD.
∴设∠B=∠C=,则∠EAD=2,
∴∠ADE=,
即∠BDH=90°-
∴∠B+∠BDH=+90°-=90°,
∴∠BHD=90°,ED⊥BC.
23、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.
求证:△ABC是等腰三角形.
【答案】
证明:过点D作DG∥AC交BC于点G,如图所示.
∵DG∥AC,∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
,∴△GDF≌△CEF(ASA),∴GD=CE.
∵BD=CE,∴BD=GD,∴∠B=∠DGB=∠ACB,∴△ABC是等腰三角形.
24、已知:
如图,
在中,,为延长线上一点,,交线段于点.
请找出一组相等的线段除外)
并加以证明
.
【解析】;
,
,,,
,,.
25、已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,
求∠B的度数.
解:∵AC=BC=BD,AD=AE,DE=CE,∴设∠ECD=∠EDC=,∠BCD=∠BDC=,
则∠AED=∠ADE=2,∠A=∠B=180°-4
在△ABC中,根据三角形内角和得,++180°-4+180°-4=180°①
又∵A、D、B在同一直线上,∴2++=180°②
由①
,②解得=36°
∴∠B=180°-4=180°-144°=36°.
26、如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线,求证:BQ+AQ=AB+BP.
证明:延长AB至E,使BE=BP,连接EP
∵在△ABC中,∠BAC=60°,∠ACB=40°,
∴∠ABC=80°∴∠E=∠BPE==40°
∵AP、BQ分别为∠BAC、∠ABC的角平分线,
∴∠QBC=40°,∠BAP=∠CAP
∴BQ=QC(等角对等边)
在△AEP与△ACP中,
,∴△AEP≌△ACP(AAS),
∴AE=AC
∴AB+BE=AQ+QC,即AB+BP=AQ+BQ.
27、问题情境:将一副直角三角板和按图1所示的方式摆放,其中,
,是的中点,点与点重合,于点,于点,试判断线段与的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
,理由如下:
连接,则是边上的中线,
∵,∴是的平分线,(依据1)
∵,,∴.(依据2)
反思交流:(1)①依据1是
;
②依据2是
;
(2)你有与小宇不同的方法吗?请写出你的方法;
(3)将图1中的沿着射线的方向平移至如图2的位置,使点落在的延长线上,的延长线与的延长线相交于点,且,的延长线与相交于点,且,连接,,试判断线段,的数量关系和位置关系,并说明理由.
(1)①等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合)
②角平分线的性质(或角平分线上的点到角两边的距离相等)
(2)有.方法如下:
∵
∵O是的中点,.
∵
在和中,
(3)
28、如图
(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别
交AB、AC于E、F两点,则图中共有_____个等腰三角形;EF与BE、CF之间的数量关系是________,△AEF的周长是________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有多少个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
【答案】
解:(1)解:BE+CF=EF.理由如下:
∵AB=AC,∴∠ABC=∠ACB.∵BD平分∠ABC,CD平分∠ACB,∴∠EBD=∠CBD,∠FCD=∠BCD,∴∠DBC=∠DCB,∴DB=DC.
∵EF∥BC,∴∠AEF=∠ABC,∠AFE=∠ACB,∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,∴BE=DE,CF=DF,AE=AF,
∴等腰三角形有△ABC,△AEF,△DEB,△DFC,△BDC共5个,
∴BE+CF=DE+DF=EF,即BE+CF=EF,△AEF的周长=AE+EF+AF=AE+BE+AF+FC=AB+AC=20.
故答案为:5;BE+CF=EF;20
(2)解:BE+CF=EF.
∵BD平分∠ABC,CD平分∠ACB,∴∠EBD=∠CBD,∠FCD=∠BCD.
∵EF∥BC,∴∠EDB=∠CBD,∠FDC=∠BCD,∴∠EBD=∠EDB,∠FDC=∠BCD,∴BE=DE,CF=DF,
∴等腰三角形有△BDE,△CFD,
∴BE+CF=DE+DF=EF,即BE+CF=EF.△AEF的周=AE+EF+AF=AE+ED+DF+AF=AE+EB+CF+AF=AB+AC=8+10=18.
此时有两个等腰三角形,EF=BE+CF,C△AEF=18
(3)解:BE﹣CF=EF.由(1)知BE=ED.∵EF∥BC,∴∠EDC=∠DCG=∠ACD,∴CF=DF.又
∵ED﹣DF=EF,∴BE﹣CF=EF.
一、选择题
1、如图,在,点在上,下列四个命题正确的有(
)
①若,则
②若,,则,
③若,,则,
④若,,则,
A.1个
B.
2个
C.
3个
D.
4个
(1)
(2)
(3)
(5)
2、如图所示,中,,是上一点,于点,若,
则的度数是
A.
B.
C.
D.
3、如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是(
)
A.60°
B.70°
C.80°
D.不确定
4、等腰三角形一腰上的高与另一腰所成的夹角为45°,则顶角的度数为(
)
A.
45°或135°
B.45°
C.135°
D.90°
5、如图,在中,和的平分线交于点,过点作,交于,交于,若,,则线段的长为
A.5
B.6
C.7
D.8
6、将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是(
)
A.
4个
B.
3个
C.
2个
D.
1个
(6)
(7)
(8)
(9)
7、如图,在中,,、两点分别在、上,是的平分线,,若,,则的周长是
A.
B.
C.
D.
8、如图,在中,,,是的平分线.若在边上截取,连接,则图中的等腰三角形共有(
)
A.
2个
B.
3个
C.
4个
D.
5个
9、如图,中,,垂直平分,,,则的度数为
A.
B.
C.
D.
10、在中,与相邻的外角是,要使为等腰三角形,则的度数是
A.
B.
C.或
D.或或
二、填空题
11、已知一个等腰三角形两边长分别为5,6,则它的周长为_________
12、等腰三角形的一个角是70°,则它的顶角的度数是
.
13、如图,A、B、C、D、E、F、G都在∠O的边上,OA=AB=BC=CD=DE=EF=FG,若∠EFG=30°,则∠O=________.
14、如图,在中,,点分别在上,且,,
若,则的度数为
.
(14)
(15)
(16)
(17)
15、如图,在△ABC中,OB、OC分别是∠ABC和∠ACB的角平分线,过点O作OE∥AB,OF∥AC,交边BC于点E、F,如果BC=10,那么C△OEF等于
.
16、如图,中,与的平分线交于点,过作交、于、,若的周长比的周长大,到的距离为,的面积
.
17、如图,在中,,点D,点E分别是BC,AC上一点,且,若,,则的度数为________.
18、如图,在中,,平分,,,、为垂足,则下列四个结论:(1);(2);(3)平分;(4)垂直平分.其中正确的有
(18)
(19)
(20)
19、如图,在△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,
则DE等于
.
20、如图,是等腰三角形,,,平分;点是射线上一点,如果
点满足是等腰三角形,那么的度数是
.
三、解答题
21、如图,在中,延长到点,使,连接,是的中线,是
的平分线.求证:
.
22、已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
23、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.
求证:△ABC是等腰三角形.
24、已知:
如图,
在中,,为延长线上一点,,交线段于点.
请找出一组相等的线段除外)
并加以证明
.
25、已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,
求∠B的度数.
26、如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线,求证:BQ+AQ=AB+BP.
27、问题情境:将一副直角三角板和按图1所示的方式摆放,其中,
,是的中点,点与点重合,于点,于点,试判断线段与的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
,理由如下:
连接,则是边上的中线,
∵,∴是的平分线,(依据1)
∵,,∴.(依据2)
反思交流:(1)①依据1是
;
②依据2是
;
(2)你有与小宇不同的方法吗?请写出你的方法;
(3)将图1中的沿着射线的方向平移至如图2的位置,使点落在的延长线上,的延长线与的延长线相交于点,且,的延长线与相交于点,且,连接,,试判断线段,的数量关系和位置关系,并说明理由.
28、如图
(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别
交AB、AC于E、F两点,则图中共有_____个等腰三角形;EF与BE、CF之间的数量关系是________,△AEF的周长是________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有多少个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
2020-2021学年度苏科版八年级上学期数学2.5等腰三角形的性质与判断专题培优训练卷
(答案)
一、选择题
1、如图,在,点在上,下列四个命题正确的有(
D
)
①若,则
②若,,则,
③若,,则,
④若,,则,
A.1个
B.
2个
C.
3个
D.
4个
2、如图所示,中,,是上一点,于点,若,
则的度数是
A.
B.
C.
D.
【解答】解:,,,
,,.故选:.
3、如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是(
C
)
A.60°
B.70°
C.80°
D.不确定
4、等腰三角形一腰上的高与另一腰所成的夹角为45°,则顶角的度数为(
A
)
A.
45°或135°
B.45°
C.135°
D.90°
5、如图,在中,和的平分线交于点,过点作,交于,交于,若,,则线段的长为
A.5
B.6
C.7
D.8
【解析】、是、的角平分线,,,
又,,,,,
,,,故选:.
6、将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是(
B
)
A.
4个
B.
3个
C.
2个
D.
1个
7、如图,在中,,、两点分别在、上,是的平分线,,若,,则的周长是
A.
B.
C.
D.
【解析】,.
,,,,
是的平分线,.,
,的周长为,
故选:.
8、如图,在中,,,是的平分线.若在边上截取,连接,则图中的等腰三角形共有(
D
)
A.
2个
B.
3个
C.
4个
D.
5个
9、如图,中,,垂直平分,,,则的度数为
A.
B.
C.
D.
【解答】解:垂直平分,,
,是等腰直角三角形,,
又,,
,
,,,,,
.
故选:.
10、在中,与相邻的外角是,要使为等腰三角形,则的度数是
A.
B.
C.或
D.或或
【解答】解:.
当时,;
当时,,则;
当时,.
的度数为或或,
故选:.
二、填空题
11、已知一个等腰三角形两边长分别为5,6,则它的周长为___16或17
______
12、等腰三角形的一个角是70°,则它的顶角的度数是
70°或40o;
.
13、如图,A、B、C、D、E、F、G都在∠O的边上,OA=AB=BC=CD=DE=EF=FG,若∠EFG=30°,则∠O=________.
解:∵∠O=x,OA=AB=BC=CD=DE=EF=FG,
∴∠BAC=2x,∴∠CBD=3x;∴∠DCE=4x,
∴∠FDE=5x,∴∠FEG=6x,
∵EF=FG,∴∠FEG=∠FGE,
∵∠EFG=30°,∴∠FEG=6x=75°,∴x=12.5o
,
∴∠O=12.5°.故答案为:12.5°.
14、如图,在中,,点分别在上,且,,
若,则的度数为
70°
.
15、如图,在△ABC中,OB、OC分别是∠ABC和∠ACB的角平分线,过点O作OE∥AB,OF∥AC,交边BC于点E、F,如果BC=10,那么C△OEF等于
10
.
16、如图,中,与的平分线交于点,过作交、于、,若的周长比的周长大,到的距离为,的面积
.
【解析】与的平分线交于点,,,
,,,
,,,,
,,
的周长比的周长大,,
,
到的距离为,的面积是.,
故答案为:
18
.
17、如图,在中,,点D,点E分别是BC,AC上一点,且,若,,则的度数为________.
解:,,
,,,
,,
,,
18、如图,在中,,平分,,,、为垂足,则下列四个结论:(1);(2);(3)平分;(4)垂直平分.其中正确的有①②③正确
19、如图,在△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,
则DE等于
.
【解析】解:∵BI、CI分别平分∠ABC、∠ACF,∴∠ABI=∠CBI,∠ECI=∠ICF,
∵DE∥BC,∴∠DIB=∠CBI,∠EIC=∠ICF,
∴∠ABI=∠DIB,∠ECI=∠EIC,
∴DI=BD=8cm,EI=CE=5cm,∴DE=DI﹣EI=3cm.
20、如图,是等腰三角形,,,平分;点是射线上一点,如果
点满足是等腰三角形,那么的度数是 、或 .
【解答】解:当时,如图所示,
,,,
平分,,,,
当时,如图所示,
,,,
平分,,,.
当时,如图所示,
,,,
平分,,,,
故答案为:、或.
三、解答题
21、如图,在中,延长到点,使,连接,是的中线,是
的平分线.求证:
.
∵CD=CA,CF是的中线,
是的平分线,
∵CE是的平分线,,
22、已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
证明:ED⊥BC;延长ED,交BC边于H,
∵AB=AC,AE=AD.
∴设∠B=∠C=,则∠EAD=2,
∴∠ADE=,
即∠BDH=90°-
∴∠B+∠BDH=+90°-=90°,
∴∠BHD=90°,ED⊥BC.
23、如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.
求证:△ABC是等腰三角形.
【答案】
证明:过点D作DG∥AC交BC于点G,如图所示.
∵DG∥AC,∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
,∴△GDF≌△CEF(ASA),∴GD=CE.
∵BD=CE,∴BD=GD,∴∠B=∠DGB=∠ACB,∴△ABC是等腰三角形.
24、已知:
如图,
在中,,为延长线上一点,,交线段于点.
请找出一组相等的线段除外)
并加以证明
.
【解析】;
,
,,,
,,.
25、已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,
求∠B的度数.
解:∵AC=BC=BD,AD=AE,DE=CE,∴设∠ECD=∠EDC=,∠BCD=∠BDC=,
则∠AED=∠ADE=2,∠A=∠B=180°-4
在△ABC中,根据三角形内角和得,++180°-4+180°-4=180°①
又∵A、D、B在同一直线上,∴2++=180°②
由①
,②解得=36°
∴∠B=180°-4=180°-144°=36°.
26、如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线,求证:BQ+AQ=AB+BP.
证明:延长AB至E,使BE=BP,连接EP
∵在△ABC中,∠BAC=60°,∠ACB=40°,
∴∠ABC=80°∴∠E=∠BPE==40°
∵AP、BQ分别为∠BAC、∠ABC的角平分线,
∴∠QBC=40°,∠BAP=∠CAP
∴BQ=QC(等角对等边)
在△AEP与△ACP中,
,∴△AEP≌△ACP(AAS),
∴AE=AC
∴AB+BE=AQ+QC,即AB+BP=AQ+BQ.
27、问题情境:将一副直角三角板和按图1所示的方式摆放,其中,
,是的中点,点与点重合,于点,于点,试判断线段与的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
,理由如下:
连接,则是边上的中线,
∵,∴是的平分线,(依据1)
∵,,∴.(依据2)
反思交流:(1)①依据1是
;
②依据2是
;
(2)你有与小宇不同的方法吗?请写出你的方法;
(3)将图1中的沿着射线的方向平移至如图2的位置,使点落在的延长线上,的延长线与的延长线相交于点,且,的延长线与相交于点,且,连接,,试判断线段,的数量关系和位置关系,并说明理由.
(1)①等腰三角形三线合一(或等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合)
②角平分线的性质(或角平分线上的点到角两边的距离相等)
(2)有.方法如下:
∵
∵O是的中点,.
∵
在和中,
(3)
28、如图
(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别
交AB、AC于E、F两点,则图中共有_____个等腰三角形;EF与BE、CF之间的数量关系是________,△AEF的周长是________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有多少个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
【答案】
解:(1)解:BE+CF=EF.理由如下:
∵AB=AC,∴∠ABC=∠ACB.∵BD平分∠ABC,CD平分∠ACB,∴∠EBD=∠CBD,∠FCD=∠BCD,∴∠DBC=∠DCB,∴DB=DC.
∵EF∥BC,∴∠AEF=∠ABC,∠AFE=∠ACB,∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,∴BE=DE,CF=DF,AE=AF,
∴等腰三角形有△ABC,△AEF,△DEB,△DFC,△BDC共5个,
∴BE+CF=DE+DF=EF,即BE+CF=EF,△AEF的周长=AE+EF+AF=AE+BE+AF+FC=AB+AC=20.
故答案为:5;BE+CF=EF;20
(2)解:BE+CF=EF.
∵BD平分∠ABC,CD平分∠ACB,∴∠EBD=∠CBD,∠FCD=∠BCD.
∵EF∥BC,∴∠EDB=∠CBD,∠FDC=∠BCD,∴∠EBD=∠EDB,∠FDC=∠BCD,∴BE=DE,CF=DF,
∴等腰三角形有△BDE,△CFD,
∴BE+CF=DE+DF=EF,即BE+CF=EF.△AEF的周=AE+EF+AF=AE+ED+DF+AF=AE+EB+CF+AF=AB+AC=8+10=18.
此时有两个等腰三角形,EF=BE+CF,C△AEF=18
(3)解:BE﹣CF=EF.由(1)知BE=ED.∵EF∥BC,∴∠EDC=∠DCG=∠ACD,∴CF=DF.又
∵ED﹣DF=EF,∴BE﹣CF=EF.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
