苏科版八年级上册数学2.5直角三角形斜边中线的性质专题培优训练卷(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册数学2.5直角三角形斜边中线的性质专题培优训练卷(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 563.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-08 00:00:00 | ||
图片预览

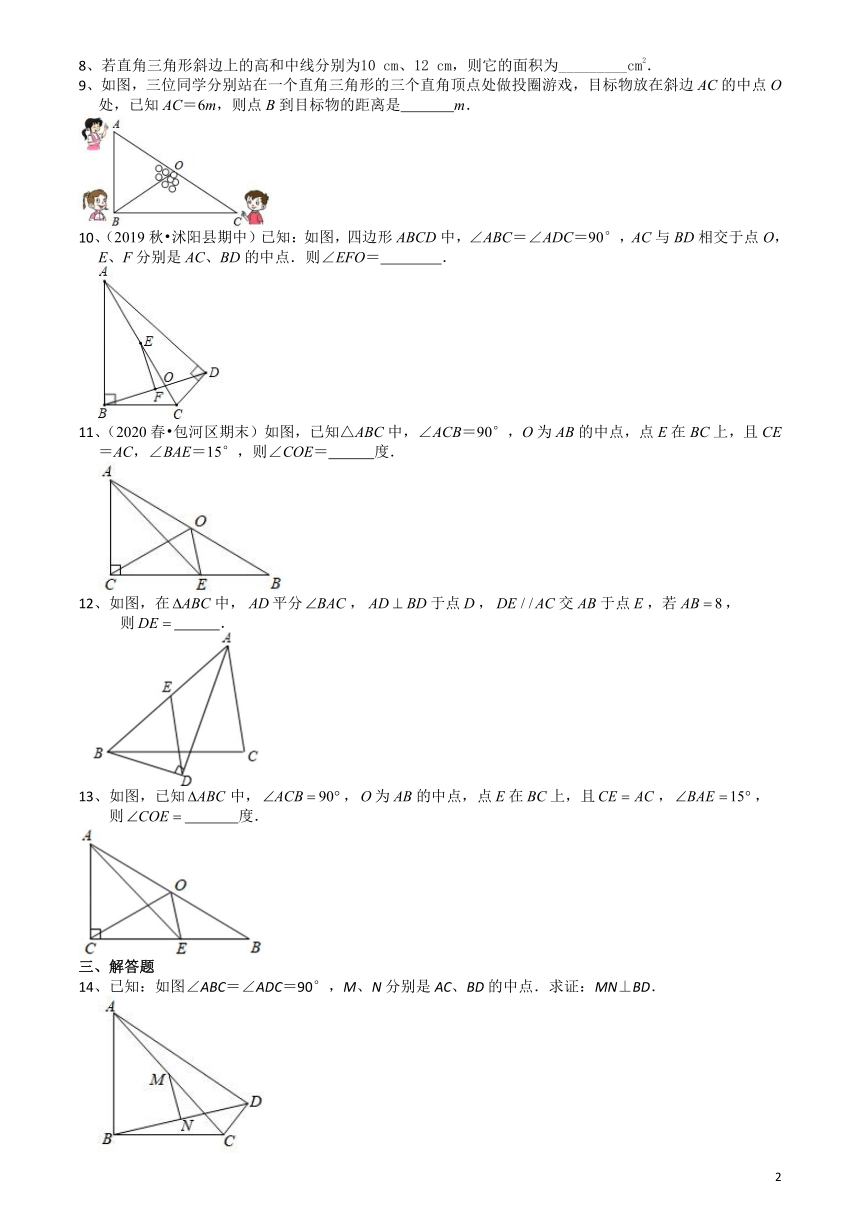
文档简介
2020-2021学年度苏科版八年级上学期数学2.5直角三角形斜边中线的性质专题培优训练卷
一、选择题
1、如图,在△ABC中,∠ACB=90°,D是AB的中点,且DC=AC,则∠B的度数是( )
A.25°
B.30°
C.45°
D.60°
2、如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF
=
5,BC
=
8,则△EFM的周长及图中的等腰三角形个数分别是( )
A.21、2
B.18、3
C.13、4
D.13、5
3、(2020春?蚌埠期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
4、如果三角形一边上的中线等于这条边的一半,则这个三角形一定是
(
)
A.等边三角形
B.直角三角形
C.等腰三角形
D.以上答案都不对
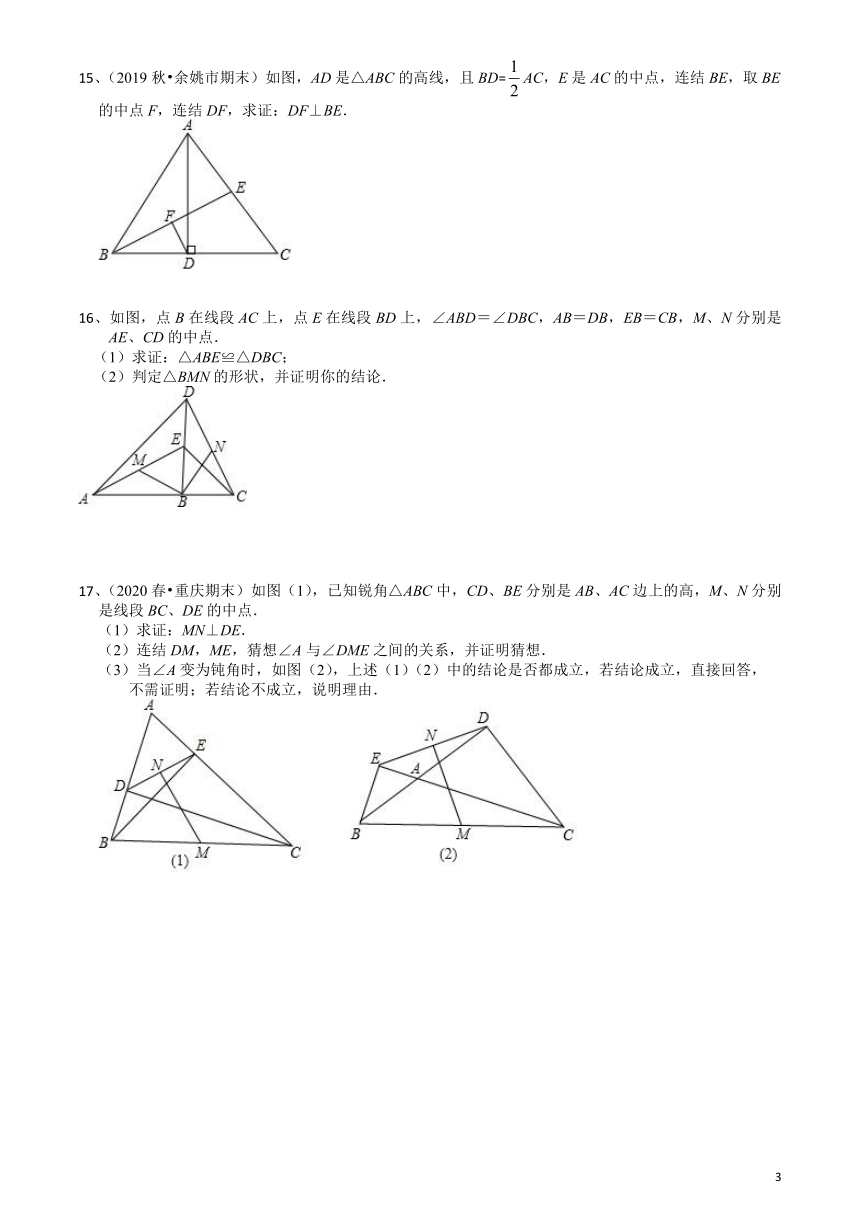
二、填空题
5、如图,△ABC和△ABD均为直角三角形,∠ACB=∠ADB=90°,E为AB的中点,CE=10.
则DE的长为________
6、如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,E是AC的中点.若DE=5,则AB的长为_______.
7、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=6
cm,则AB=_______cm.
8、若直角三角形斜边上的高和中线分别为10
cm、12
cm,则它的面积为_________cm2.
9、如图,三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知AC=6m,则点B到目标物的距离是
m.
10、(2019秋?沭阳县期中)已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=
.
11、(2020春?包河区期末)如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E在BC上,且CE=AC,∠BAE=15°,则∠COE=
度.
12、如图,在中,平分,于点,交于点,若,
则
.
13、如图,已知中,,为的中点,点在上,且,,
则
度.
三、解答题
14、已知:如图∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
15、(2019秋?余姚市期末)如图,AD是△ABC的高线,且BD=AC,E是AC的中点,连结BE,取BE的中点F,连结DF,求证:DF⊥BE.
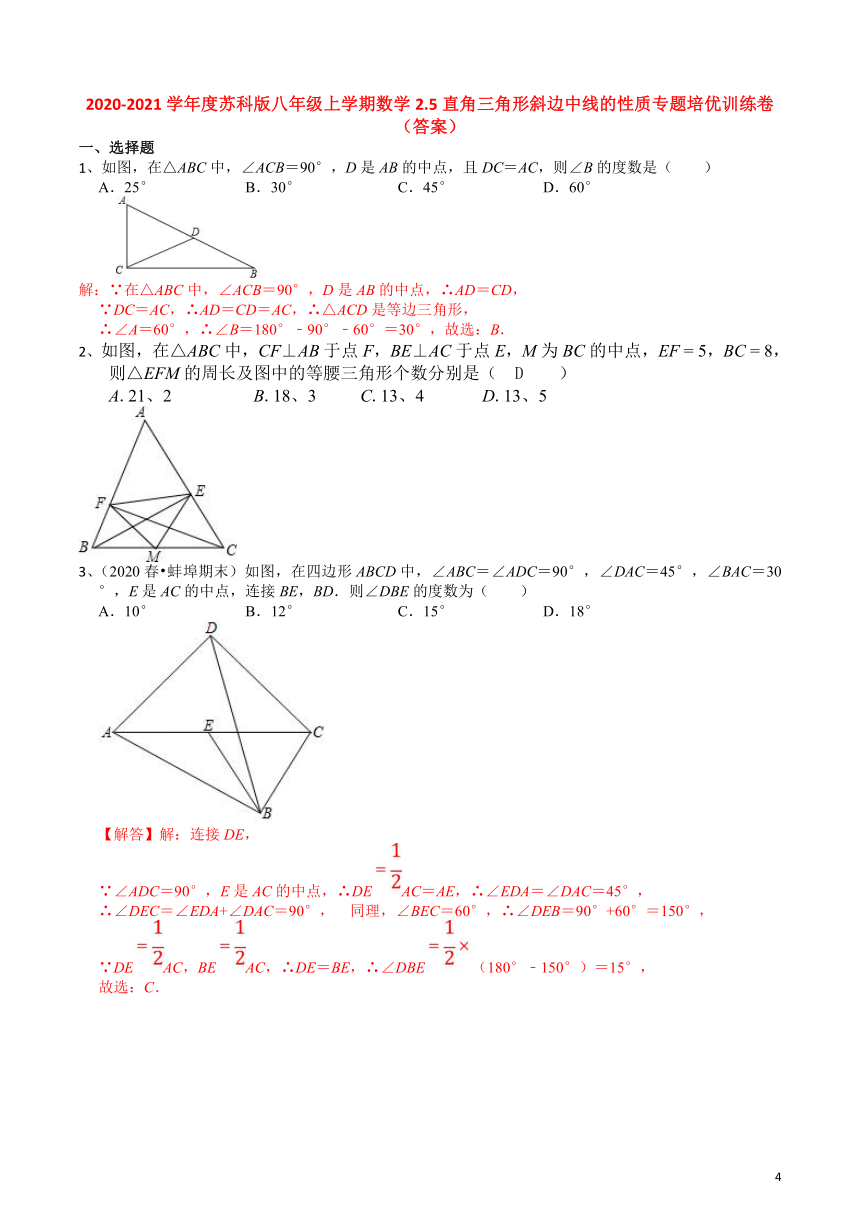
16、如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点.
(1)求证:△ABE≌△DBC;
(2)判定△BMN的形状,并证明你的结论.
17、(2020春?重庆期末)如图(1),已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,
不需证明;若结论不成立,说明理由.
2020-2021学年度苏科版八年级上学期数学2.5直角三角形斜边中线的性质专题培优训练卷(答案)
一、选择题
1、如图,在△ABC中,∠ACB=90°,D是AB的中点,且DC=AC,则∠B的度数是( )
A.25°
B.30°
C.45°
D.60°
解:∵在△ABC中,∠ACB=90°,D是AB的中点,∴AD=CD,
∵DC=AC,∴AD=CD=AC,∴△ACD是等边三角形,
∴∠A=60°,∴∠B=180°﹣90°﹣60°=30°,故选:B.
2、如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF
=
5,BC
=
8,则△EFM的周长及图中的等腰三角形个数分别是( D )
A.21、2
B.18、3
C.13、4
D.13、5
3、(2020春?蚌埠期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
【解答】解:连接DE,
∵∠ADC=90°,E是AC的中点,∴DEAC=AE,∴∠EDA=∠DAC=45°,
∴∠DEC=∠EDA+∠DAC=90°,
同理,∠BEC=60°,∴∠DEB=90°+60°=150°,
∵DEAC,BEAC,∴DE=BE,∴∠DBE(180°﹣150°)=15°,
故选:C.
4、如果三角形一边上的中线等于这条边的一半,则这个三角形一定是
(
B
)
A.等边三角形
B.直角三角形
C.等腰三角形
D.以上答案都不对
二、填空题
5、如图,△ABC和△ABD均为直角三角形,∠ACB=∠ADB=90°,E为AB的中点,CE=10.
则DE的长为___10_____
6、如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,E是AC的中点.若DE=5,则AB的长为___10____.
7、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=6
cm,则AB=__12______cm.
8、若直角三角形斜边上的高和中线分别为10
cm、12
cm,则它的面积为___120_______cm2.
9、如图,三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知AC=6m,则点B到目标物的距离是
m.
解:∵∠ABC=90°,点O是斜边AC的中点,
∴BO=AC=3m,
故答案为:3.
10、(2019秋?沭阳县期中)已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=
.
【分析】连接EB、ED,根据直角三角形的性质得到EB=ED,根据等腰三角形的性质得到答案.
【答案】解:连接EB、ED,
∵∠ABC=90°,E是AC的中点,∴BEAC,
同理,DEAC,∴EB=ED,又F是BD的中点,
∴EF⊥BD,∴∠EFO=90°,故答案为:90°.
11、(2020春?包河区期末)如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E在BC上,且CE=AC,∠BAE=15°,则∠COE=
度.
【解答】解:∵∠ACB=90°,CE=AC,∴∠CAE=∠AEC=45°,
∵∠BAE=15°,∴∠CAB=60°,∴∠B=30°,
∵∠ACB=90°,O为AB的中点,∴CO=BO=AOAB,
∴△AOC是等边三角形,∠OCB=∠B=30°,∴AC=OC=CE,
∴∠COE=∠CEO(180°﹣30°)=75°,
故答案为:75.
12、如图,在中,平分,于点,交于点,若,
则
.
【解答】是的平分线,,
,,,,
,,,,,
,.故答案为:4.
13、如图,已知中,,为的中点,点在上,且,,
则 75 度.
【解答】,,,
,,,
,为的中点,,
是等边三角形,,,
,故答案为:75.
三、解答题
14、已知:如图∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
证明:如图,连接BM、DM,
∵∠ABC=∠ADC=90°,M是AC的中点,∴BM=DM=AC,
∵点N是BD的中点,∴MN⊥BD.
(10分)
15、(2019秋?余姚市期末)如图,AD是△ABC的高线,且BDAC,E是AC的中点,连结BE,取BE的中点F,连结DF,求证:DF⊥BE.
【解答】证明:连结DE,
∵AD是△ABC的高线,E是AC的中点,∴,
又∵,∴DE=BD.
又∵F是BE的中点,∴DF⊥BE.
16、如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点.
(1)求证:△ABE≌△DBC;
(2)判定△BMN的形状,并证明你的结论.
【答案】解:(1)在△ABE和△DBC中,∵,∴△ABE≌△DBC(SAS)
(2)△MBN是等腰直角三角形
证明如下:∵△ABE≌△DBC∴AE=CD,∠BAM=∠BDN
∵M,N分别是AE,CD的中点,∴AM=AE,CN=CD,∴AM=CN
在△ABM和△DBN中,∵∴ABM≌△DBN(SAS)
∴BM=BN,∠ABM=∠DBN
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,∴∠ABD=∠ABM+∠DBM=90°
∴∠DBN+∠DBM=∠MBN=90°,∴△MBN是等腰直角三角形
17、(2020春?重庆期末)如图(1),已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,
不需证明;若结论不成立,说明理由.
【解答】(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,∴DMBC,MEBC,∴DM=ME,
又∵N为DE中点,∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)=360°﹣2(∠ABC+∠ACB),
=360°﹣2(180°﹣∠A)=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连结DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°﹣∠BAC)=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC)=2∠BAC﹣180°.
一、选择题
1、如图,在△ABC中,∠ACB=90°,D是AB的中点,且DC=AC,则∠B的度数是( )
A.25°
B.30°
C.45°
D.60°
2、如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF
=
5,BC
=
8,则△EFM的周长及图中的等腰三角形个数分别是( )
A.21、2
B.18、3
C.13、4
D.13、5
3、(2020春?蚌埠期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
4、如果三角形一边上的中线等于这条边的一半,则这个三角形一定是
(
)
A.等边三角形
B.直角三角形
C.等腰三角形
D.以上答案都不对
二、填空题
5、如图,△ABC和△ABD均为直角三角形,∠ACB=∠ADB=90°,E为AB的中点,CE=10.
则DE的长为________
6、如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,E是AC的中点.若DE=5,则AB的长为_______.
7、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=6
cm,则AB=_______cm.
8、若直角三角形斜边上的高和中线分别为10
cm、12
cm,则它的面积为_________cm2.
9、如图,三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知AC=6m,则点B到目标物的距离是
m.
10、(2019秋?沭阳县期中)已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=
.
11、(2020春?包河区期末)如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E在BC上,且CE=AC,∠BAE=15°,则∠COE=
度.
12、如图,在中,平分,于点,交于点,若,
则
.
13、如图,已知中,,为的中点,点在上,且,,
则
度.
三、解答题
14、已知:如图∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
15、(2019秋?余姚市期末)如图,AD是△ABC的高线,且BD=AC,E是AC的中点,连结BE,取BE的中点F,连结DF,求证:DF⊥BE.
16、如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点.
(1)求证:△ABE≌△DBC;
(2)判定△BMN的形状,并证明你的结论.
17、(2020春?重庆期末)如图(1),已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,
不需证明;若结论不成立,说明理由.
2020-2021学年度苏科版八年级上学期数学2.5直角三角形斜边中线的性质专题培优训练卷(答案)
一、选择题
1、如图,在△ABC中,∠ACB=90°,D是AB的中点,且DC=AC,则∠B的度数是( )
A.25°
B.30°
C.45°
D.60°
解:∵在△ABC中,∠ACB=90°,D是AB的中点,∴AD=CD,
∵DC=AC,∴AD=CD=AC,∴△ACD是等边三角形,
∴∠A=60°,∴∠B=180°﹣90°﹣60°=30°,故选:B.
2、如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF
=
5,BC
=
8,则△EFM的周长及图中的等腰三角形个数分别是( D )
A.21、2
B.18、3
C.13、4
D.13、5
3、(2020春?蚌埠期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )
A.10°
B.12°
C.15°
D.18°
【解答】解:连接DE,
∵∠ADC=90°,E是AC的中点,∴DEAC=AE,∴∠EDA=∠DAC=45°,
∴∠DEC=∠EDA+∠DAC=90°,
同理,∠BEC=60°,∴∠DEB=90°+60°=150°,
∵DEAC,BEAC,∴DE=BE,∴∠DBE(180°﹣150°)=15°,
故选:C.
4、如果三角形一边上的中线等于这条边的一半,则这个三角形一定是
(
B
)
A.等边三角形
B.直角三角形
C.等腰三角形
D.以上答案都不对
二、填空题
5、如图,△ABC和△ABD均为直角三角形,∠ACB=∠ADB=90°,E为AB的中点,CE=10.
则DE的长为___10_____
6、如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,E是AC的中点.若DE=5,则AB的长为___10____.
7、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=6
cm,则AB=__12______cm.
8、若直角三角形斜边上的高和中线分别为10
cm、12
cm,则它的面积为___120_______cm2.
9、如图,三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知AC=6m,则点B到目标物的距离是
m.
解:∵∠ABC=90°,点O是斜边AC的中点,
∴BO=AC=3m,
故答案为:3.
10、(2019秋?沭阳县期中)已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=
.
【分析】连接EB、ED,根据直角三角形的性质得到EB=ED,根据等腰三角形的性质得到答案.
【答案】解:连接EB、ED,
∵∠ABC=90°,E是AC的中点,∴BEAC,
同理,DEAC,∴EB=ED,又F是BD的中点,
∴EF⊥BD,∴∠EFO=90°,故答案为:90°.
11、(2020春?包河区期末)如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E在BC上,且CE=AC,∠BAE=15°,则∠COE=
度.
【解答】解:∵∠ACB=90°,CE=AC,∴∠CAE=∠AEC=45°,
∵∠BAE=15°,∴∠CAB=60°,∴∠B=30°,
∵∠ACB=90°,O为AB的中点,∴CO=BO=AOAB,
∴△AOC是等边三角形,∠OCB=∠B=30°,∴AC=OC=CE,
∴∠COE=∠CEO(180°﹣30°)=75°,
故答案为:75.
12、如图,在中,平分,于点,交于点,若,
则
.
【解答】是的平分线,,
,,,,
,,,,,
,.故答案为:4.
13、如图,已知中,,为的中点,点在上,且,,
则 75 度.
【解答】,,,
,,,
,为的中点,,
是等边三角形,,,
,故答案为:75.
三、解答题
14、已知:如图∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
证明:如图,连接BM、DM,
∵∠ABC=∠ADC=90°,M是AC的中点,∴BM=DM=AC,
∵点N是BD的中点,∴MN⊥BD.
(10分)
15、(2019秋?余姚市期末)如图,AD是△ABC的高线,且BDAC,E是AC的中点,连结BE,取BE的中点F,连结DF,求证:DF⊥BE.
【解答】证明:连结DE,
∵AD是△ABC的高线,E是AC的中点,∴,
又∵,∴DE=BD.
又∵F是BE的中点,∴DF⊥BE.
16、如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点.
(1)求证:△ABE≌△DBC;
(2)判定△BMN的形状,并证明你的结论.
【答案】解:(1)在△ABE和△DBC中,∵,∴△ABE≌△DBC(SAS)
(2)△MBN是等腰直角三角形
证明如下:∵△ABE≌△DBC∴AE=CD,∠BAM=∠BDN
∵M,N分别是AE,CD的中点,∴AM=AE,CN=CD,∴AM=CN
在△ABM和△DBN中,∵∴ABM≌△DBN(SAS)
∴BM=BN,∠ABM=∠DBN
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,∴∠ABD=∠ABM+∠DBM=90°
∴∠DBN+∠DBM=∠MBN=90°,∴△MBN是等腰直角三角形
17、(2020春?重庆期末)如图(1),已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,
不需证明;若结论不成立,说明理由.
【解答】(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,∴DMBC,MEBC,∴DM=ME,
又∵N为DE中点,∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)=360°﹣2(∠ABC+∠ACB),
=360°﹣2(180°﹣∠A)=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连结DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°﹣∠BAC)=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC)=2∠BAC﹣180°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
