华师大版八年级数学上册 第13章 全等三角形测试题(含答案)
文档属性
| 名称 | 华师大版八年级数学上册 第13章 全等三角形测试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 644.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-08 00:00:00 | ||
图片预览

文档简介
第13章 全等三角形测试题
(本试卷满分100分)
一、选择题(每小题3分,共30分)
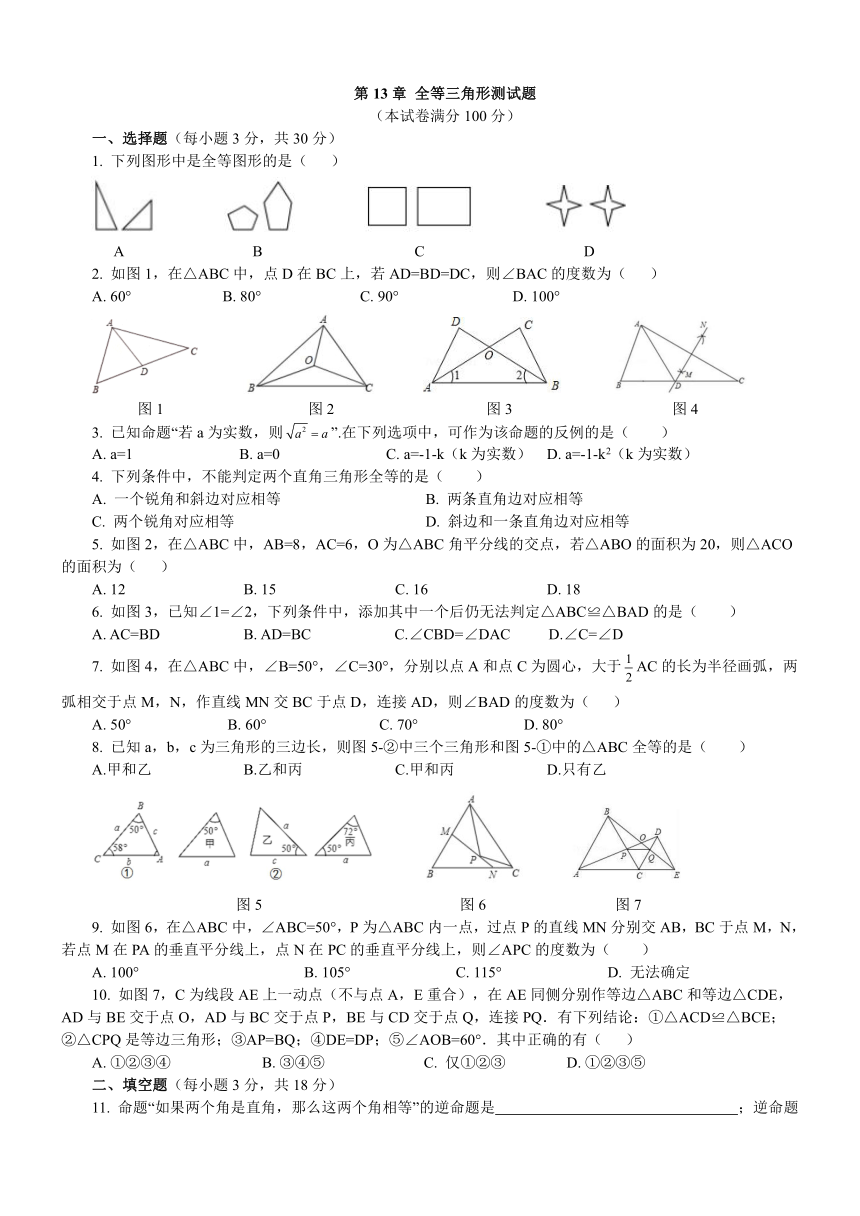
1. 下列图形中是全等图形的是( )
A B C D
2. 如图1,在△ABC中,点D在BC上,若AD=BD=DC,则∠BAC的度数为( )
A. 60° B. 80° C. 90° D. 100°
图1 图2 图3 图4
3. 已知命题“若a为实数,则”.在下列选项中,可作为该命题的反例的是( )
A. a=1 B. a=0 C. a=-1-k(k为实数) D. a=-1-k2(k为实数)
4. 下列条件中,不能判定两个直角三角形全等的是( )
A. 一个锐角和斜边对应相等 B. 两条直角边对应相等
C. 两个锐角对应相等 D. 斜边和一条直角边对应相等
5. 如图2,在△ABC中,AB=8,AC=6,O为△ABC角平分线的交点,若△ABO的面积为20,则△ACO的面积为( )
A. 12 B. 15 C. 16 D. 18
6. 如图3,已知∠1=∠2,下列条件中,添加其中一个后仍无法判定△ABC≌△BAD的是( )
A. AC=BD B. AD=BC C.∠CBD=∠DAC D.∠C=∠D
7. 如图4,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为( )
A. 50° B. 60° C. 70° D. 80°
8. 已知a,b,c为三角形的三边长,则图5-②中三个三角形和图5-①中的△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有乙
图5 图6 图7
9. 如图6,在△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N,若点M在PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数为( )
A. 100° B. 105° C. 115° D. 无法确定
10. 如图7,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.有下列结论:①△ACD≌△BCE;②△CPQ是等边三角形;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中正确的有( )
A. ①②③④ B. ③④⑤ C. 仅①②③ D. ①②③⑤
二、填空题(每小题3分,共18分)
11. 命题“如果两个角是直角,那么这两个角相等”的逆命题是 ;逆命题是 命题.(填“真”或“假”)
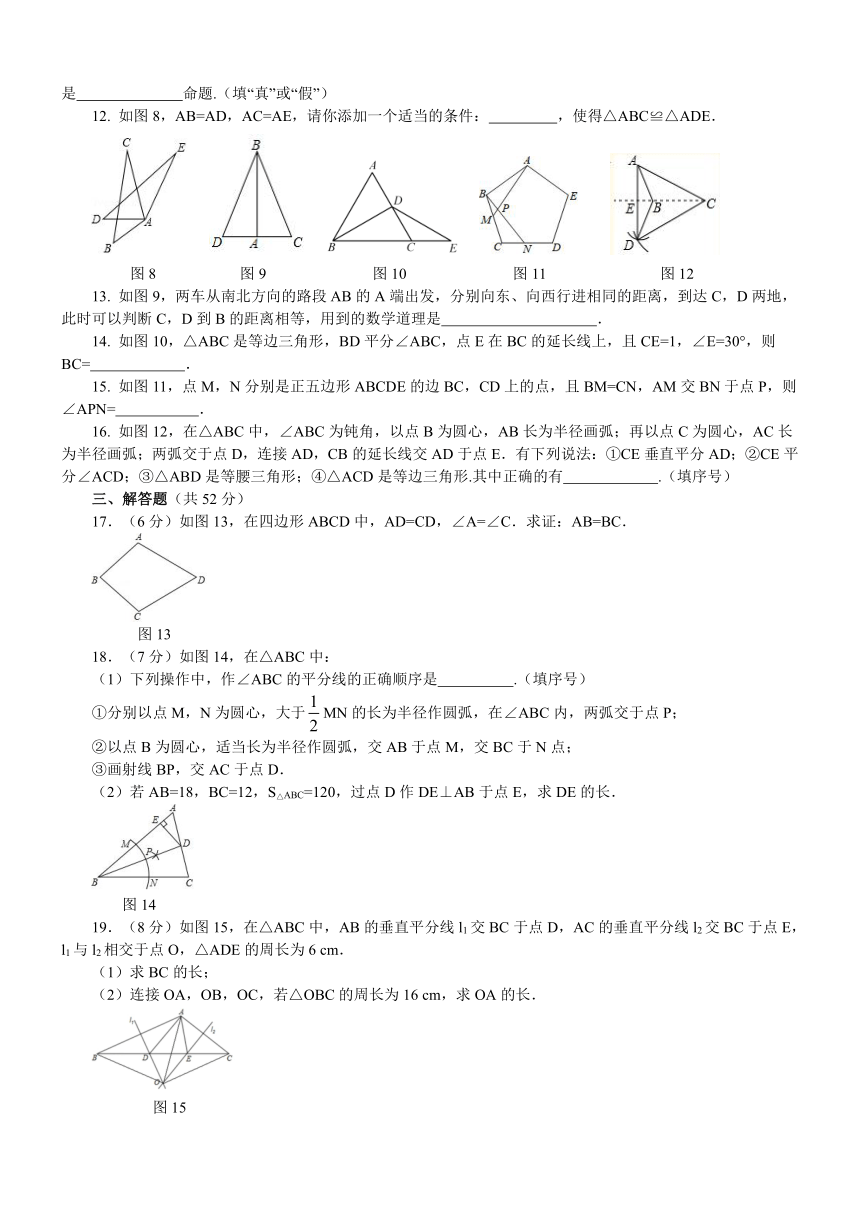
12. 如图8,AB=AD,AC=AE,请你添加一个适当的条件: ,使得△ABC≌△ADE.
图8 图9 图10 图11 图12
13. 如图9,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是 ?.
14. 如图10,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC= ?.
15. 如图11,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P,则∠APN= .
16. 如图12,在△ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.有下列说法:①CE垂直平分AD;②CE平分∠ACD;③△ABD是等腰三角形;④△ACD是等边三角形.其中正确的有 ?.(填序号)
三、解答题(共52分)
17.(6分)如图13,在四边形ABCD中,AD=CD,∠A=∠C.求证:AB=BC.
图13
18.(7分)如图14,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是 .(填序号)
①分别以点M,N为圆心,大于MN的长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于N点;
③画射线BP,交AC于点D.
(2)若AB=18,BC=12,S△ABC=120,过点D作DE⊥AB于点E,求DE的长.
图14
19.(8分)如图15,在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6 cm.
(1)求BC的长;
(2)连接OA,OB,OC,若△OBC的周长为16 cm,求OA的长.
图15
20.(9分)如图16,EG∥AF,有下列条件:①AB=AC;②DE=DF;③BE=CF .请从这三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并选择一个命题进行证明.
图16
21.(10分)图17是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=3 m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2 m,点A到地面的距离AE=1.8 m;当他从A处摆动到A′处时,有A'B⊥AB.
(1)求A′到BD的距离;
(2)求A′到地面的距离.
图17
22.(12分)如图18,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:EF=DF.
图18
附加题(20分,不计入总分)
23. 学习了三角形全等的判定方法(即“S.A.S.”“A.S.A.”“A.A.S.”“S.S.S.”)和直角三角形全等的判定方法(即“H.L.”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪想:要想解决问题,应该对∠B进行分类研究.
∠B可分为“直角、钝角、锐角”三种情况进行探究.
(1)当∠B是直角时,如图19-①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,则Rt△ABC≌Rt△DEF,其依据是 .
(2)当∠B是锐角时,如图19-②,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 .
A. 全等 B. 不全等 C. 不一定全等
(3)第三种情况:当∠B是钝角时,如图19-③,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°,求证:△ABC≌△DEF.
图19
参考答案
第13章 全等三角形测试题
一、1. D 2. C 3. D 4. C 5. B 6. B 7. C 8. B 9. C 10. D
二、11. 如果两个角相等,那么这两个角是直角 假 12. 答案不唯一,如:BC=DE
13. 线段垂直平分线上的点到线段两端点的距离相等 14. 2 15. 108° 16. ①②③
三、17. 证明:连接AC.因为AD=CD,所以∠DAC=∠DCA.因为∠BAD=∠BCD,所以∠BAC=
∠BCA.所以AB=BC.
18. 解:(1)②①③
(2)如图1,过点D作DF⊥BC于点F. 因为∠ABD=∠CBD,DE⊥AB,DF⊥BC,所以DE=DF.
因为S△ABC=S△ABD+S△CBD=×AB×DE+×BC×DF=120,
所以×18×DE+×12×DE=120,解得DE=8.所以DE=8.
19. 解:(1)因为l1,l2分别是AB,AC的垂直平分线,所以AD=BD,AE=CE.
所以AD+DE+AE=BD+DE+CE=BC.
因为△ADE的周长为6 cm,即AD+DE+AE=6 cm,所以BC=6 cm.
(2)因为l1,l2分别是AB,AC的垂直平分线,所以OA=OC=OB.
因为△OBC的周长为16 cm,即OC+OB+BC=16 cm,所以OC+OB=16-6=10 cm.所以OC=5 cm.所以OA=OC=OB=5 cm.
20. 解:命题1:因为EG//AF,AB=AC,DE=DF,所以BE=CF;
命题2:因为EG//AF,DE=DF,BE=CF,所以AB=AC;
命题3:因为EG//AF,AB=AC,BE=CF,所以DE=DF;
证明命题1,
已知:如图,EG∥AF,AB=AC,DE=DF.求证:BE=CF.
证明:因为EG∥AF,所以∠EGB=∠ACB,∠GED=∠CFD.
因为AB=AC,所以∠B=∠ACB.所以∠B=∠EGB.所以EB=EG.
在△EGD和△FCD中,∠GED=∠CFD,DE=DF,∠GDE=∠CDF,所以△EGD≌△FCD.所以EG=CF.所以BE=CF.
21.解:(1)如图2,作A′F⊥BD,垂足为点F.因为AC⊥BD,所以∠ACB=∠A′FB=90°.
在Rt△A′FB中,∠1+∠3=90°.又因为A'B⊥AB,所以∠1+∠2=90°.所以∠2=∠3.
在△ACB和△BFA′中,∠ACB=∠A′FB,∠2=∠3,AB=A'B,
所以△ACB≌△BFA′.所以A'F=BC.
因为AC∥DE且CD⊥AC,AE⊥DE,所以CD=AE=1.8 m.
所以BC=BD-CD=3-1.8=1.2 m.所以A'F=1.2 m,即A′到BD的距离是1.2 m.
(2)由(1)知△ACB≌△BFA′.所以BF=AC=2m.
作A'H⊥DE,垂足为H.
因为A'F∥DE,所以A'H=FD.所以A′H=BD-BF=3-2=1 m.即A′到地面的距离是1m.
22. 证明:连接BF,如图3.
因为点F是角平分线的交点,所以BF也是角平分线.
又因为FM⊥AB,FN⊥BC,所以MF=NF,∠DNF=∠EMF=90°.
在Rt△ABC中,∠ACB=90°,∠ABC=60°,则∠BAC=30°,
所以∠DAC=∠BAC=15°.所以∠NDF=90°-∠DAC=75°.
又因为∠MEF=∠BAC+∠ACE=75°,所以∠MEF=∠NDF.
在△EMF和△NDF中,∠EMF=∠DNF,∠MEF=∠NDF,MF=NF,所以△EMF≌△NDF.所以EF=DF.
23.解:(1)HL.
(2)C 作图如图4:
图4 图5
(3)如图5,过点C作CM⊥AB交AB的延长线于点M,过点F作FN⊥DE交DE的延长线于点N.
因为∠CBA=∠FED,所以180°-∠CBA=180°-∠FED,即∠CBM=∠FEN.
在△CBM和△FEN中,∠CBM=∠FEN,∠CMB=∠FNE,BC=EF,所以△CBM≌△FEN.
所以CM=FN.
在Rt△ACM和Rt△DFN中,AC=DF,CM=FN,所以Rt△ACM≌Rt△DFN.所以∠A=∠D.
在△ABC和△DEF中,∠A=∠D,∠CBA=∠FED,AC=DF,所以△ABC≌△DEF.
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1. 下列图形中是全等图形的是( )
A B C D
2. 如图1,在△ABC中,点D在BC上,若AD=BD=DC,则∠BAC的度数为( )
A. 60° B. 80° C. 90° D. 100°
图1 图2 图3 图4
3. 已知命题“若a为实数,则”.在下列选项中,可作为该命题的反例的是( )
A. a=1 B. a=0 C. a=-1-k(k为实数) D. a=-1-k2(k为实数)
4. 下列条件中,不能判定两个直角三角形全等的是( )
A. 一个锐角和斜边对应相等 B. 两条直角边对应相等
C. 两个锐角对应相等 D. 斜边和一条直角边对应相等
5. 如图2,在△ABC中,AB=8,AC=6,O为△ABC角平分线的交点,若△ABO的面积为20,则△ACO的面积为( )
A. 12 B. 15 C. 16 D. 18
6. 如图3,已知∠1=∠2,下列条件中,添加其中一个后仍无法判定△ABC≌△BAD的是( )
A. AC=BD B. AD=BC C.∠CBD=∠DAC D.∠C=∠D
7. 如图4,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为( )
A. 50° B. 60° C. 70° D. 80°
8. 已知a,b,c为三角形的三边长,则图5-②中三个三角形和图5-①中的△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有乙
图5 图6 图7
9. 如图6,在△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N,若点M在PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数为( )
A. 100° B. 105° C. 115° D. 无法确定
10. 如图7,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.有下列结论:①△ACD≌△BCE;②△CPQ是等边三角形;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中正确的有( )
A. ①②③④ B. ③④⑤ C. 仅①②③ D. ①②③⑤
二、填空题(每小题3分,共18分)
11. 命题“如果两个角是直角,那么这两个角相等”的逆命题是 ;逆命题是 命题.(填“真”或“假”)
12. 如图8,AB=AD,AC=AE,请你添加一个适当的条件: ,使得△ABC≌△ADE.
图8 图9 图10 图11 图12
13. 如图9,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是 ?.
14. 如图10,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC= ?.
15. 如图11,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P,则∠APN= .
16. 如图12,在△ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.有下列说法:①CE垂直平分AD;②CE平分∠ACD;③△ABD是等腰三角形;④△ACD是等边三角形.其中正确的有 ?.(填序号)
三、解答题(共52分)
17.(6分)如图13,在四边形ABCD中,AD=CD,∠A=∠C.求证:AB=BC.
图13
18.(7分)如图14,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是 .(填序号)
①分别以点M,N为圆心,大于MN的长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于N点;
③画射线BP,交AC于点D.
(2)若AB=18,BC=12,S△ABC=120,过点D作DE⊥AB于点E,求DE的长.
图14
19.(8分)如图15,在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6 cm.
(1)求BC的长;
(2)连接OA,OB,OC,若△OBC的周长为16 cm,求OA的长.
图15
20.(9分)如图16,EG∥AF,有下列条件:①AB=AC;②DE=DF;③BE=CF .请从这三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并选择一个命题进行证明.
图16
21.(10分)图17是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=3 m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2 m,点A到地面的距离AE=1.8 m;当他从A处摆动到A′处时,有A'B⊥AB.
(1)求A′到BD的距离;
(2)求A′到地面的距离.
图17
22.(12分)如图18,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:EF=DF.
图18
附加题(20分,不计入总分)
23. 学习了三角形全等的判定方法(即“S.A.S.”“A.S.A.”“A.A.S.”“S.S.S.”)和直角三角形全等的判定方法(即“H.L.”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪想:要想解决问题,应该对∠B进行分类研究.
∠B可分为“直角、钝角、锐角”三种情况进行探究.
(1)当∠B是直角时,如图19-①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,则Rt△ABC≌Rt△DEF,其依据是 .
(2)当∠B是锐角时,如图19-②,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 .
A. 全等 B. 不全等 C. 不一定全等
(3)第三种情况:当∠B是钝角时,如图19-③,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°,求证:△ABC≌△DEF.
图19
参考答案
第13章 全等三角形测试题
一、1. D 2. C 3. D 4. C 5. B 6. B 7. C 8. B 9. C 10. D
二、11. 如果两个角相等,那么这两个角是直角 假 12. 答案不唯一,如:BC=DE
13. 线段垂直平分线上的点到线段两端点的距离相等 14. 2 15. 108° 16. ①②③
三、17. 证明:连接AC.因为AD=CD,所以∠DAC=∠DCA.因为∠BAD=∠BCD,所以∠BAC=
∠BCA.所以AB=BC.
18. 解:(1)②①③
(2)如图1,过点D作DF⊥BC于点F. 因为∠ABD=∠CBD,DE⊥AB,DF⊥BC,所以DE=DF.
因为S△ABC=S△ABD+S△CBD=×AB×DE+×BC×DF=120,
所以×18×DE+×12×DE=120,解得DE=8.所以DE=8.
19. 解:(1)因为l1,l2分别是AB,AC的垂直平分线,所以AD=BD,AE=CE.
所以AD+DE+AE=BD+DE+CE=BC.
因为△ADE的周长为6 cm,即AD+DE+AE=6 cm,所以BC=6 cm.
(2)因为l1,l2分别是AB,AC的垂直平分线,所以OA=OC=OB.
因为△OBC的周长为16 cm,即OC+OB+BC=16 cm,所以OC+OB=16-6=10 cm.所以OC=5 cm.所以OA=OC=OB=5 cm.
20. 解:命题1:因为EG//AF,AB=AC,DE=DF,所以BE=CF;
命题2:因为EG//AF,DE=DF,BE=CF,所以AB=AC;
命题3:因为EG//AF,AB=AC,BE=CF,所以DE=DF;
证明命题1,
已知:如图,EG∥AF,AB=AC,DE=DF.求证:BE=CF.
证明:因为EG∥AF,所以∠EGB=∠ACB,∠GED=∠CFD.
因为AB=AC,所以∠B=∠ACB.所以∠B=∠EGB.所以EB=EG.
在△EGD和△FCD中,∠GED=∠CFD,DE=DF,∠GDE=∠CDF,所以△EGD≌△FCD.所以EG=CF.所以BE=CF.
21.解:(1)如图2,作A′F⊥BD,垂足为点F.因为AC⊥BD,所以∠ACB=∠A′FB=90°.
在Rt△A′FB中,∠1+∠3=90°.又因为A'B⊥AB,所以∠1+∠2=90°.所以∠2=∠3.
在△ACB和△BFA′中,∠ACB=∠A′FB,∠2=∠3,AB=A'B,
所以△ACB≌△BFA′.所以A'F=BC.
因为AC∥DE且CD⊥AC,AE⊥DE,所以CD=AE=1.8 m.
所以BC=BD-CD=3-1.8=1.2 m.所以A'F=1.2 m,即A′到BD的距离是1.2 m.
(2)由(1)知△ACB≌△BFA′.所以BF=AC=2m.
作A'H⊥DE,垂足为H.
因为A'F∥DE,所以A'H=FD.所以A′H=BD-BF=3-2=1 m.即A′到地面的距离是1m.
22. 证明:连接BF,如图3.
因为点F是角平分线的交点,所以BF也是角平分线.
又因为FM⊥AB,FN⊥BC,所以MF=NF,∠DNF=∠EMF=90°.
在Rt△ABC中,∠ACB=90°,∠ABC=60°,则∠BAC=30°,
所以∠DAC=∠BAC=15°.所以∠NDF=90°-∠DAC=75°.
又因为∠MEF=∠BAC+∠ACE=75°,所以∠MEF=∠NDF.
在△EMF和△NDF中,∠EMF=∠DNF,∠MEF=∠NDF,MF=NF,所以△EMF≌△NDF.所以EF=DF.
23.解:(1)HL.
(2)C 作图如图4:
图4 图5
(3)如图5,过点C作CM⊥AB交AB的延长线于点M,过点F作FN⊥DE交DE的延长线于点N.
因为∠CBA=∠FED,所以180°-∠CBA=180°-∠FED,即∠CBM=∠FEN.
在△CBM和△FEN中,∠CBM=∠FEN,∠CMB=∠FNE,BC=EF,所以△CBM≌△FEN.
所以CM=FN.
在Rt△ACM和Rt△DFN中,AC=DF,CM=FN,所以Rt△ACM≌Rt△DFN.所以∠A=∠D.
在△ABC和△DEF中,∠A=∠D,∠CBA=∠FED,AC=DF,所以△ABC≌△DEF.
