3.2函数的基本性质第三课时 教案(word)
文档属性
| 名称 | 3.2函数的基本性质第三课时 教案(word) |
|
|
| 格式 | doc | ||
| 文件大小 | 359.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-08 00:00:00 | ||
图片预览

文档简介
《3.2 函数的基本性质(第三课时)》教学设计
教学目标
1.能类比单调性的探究思路,抽象出函数奇偶性的定义,提升学生的直观想象素养和数学抽象素养;了解奇函数与偶函数的定义和图象特征,能从函数图象直观判断函数是否具有奇偶性.
2.能根据函数奇偶性的定义判断函数的奇偶性;能利用函数的奇偶性帮助画函数图象和计算函数值,提升学生的逻辑推理和数学运算素养.
教学重难点
教学重点:了解奇函数与偶函数的定义和图象特征,根据函数奇偶性的定义判断函数的奇偶性.
教学难点:“图象关于y轴(原点)对称”转化为定量的符号语言.
课前准备
用软件制作动画;PPT课件.
教学过程
一、问题导入
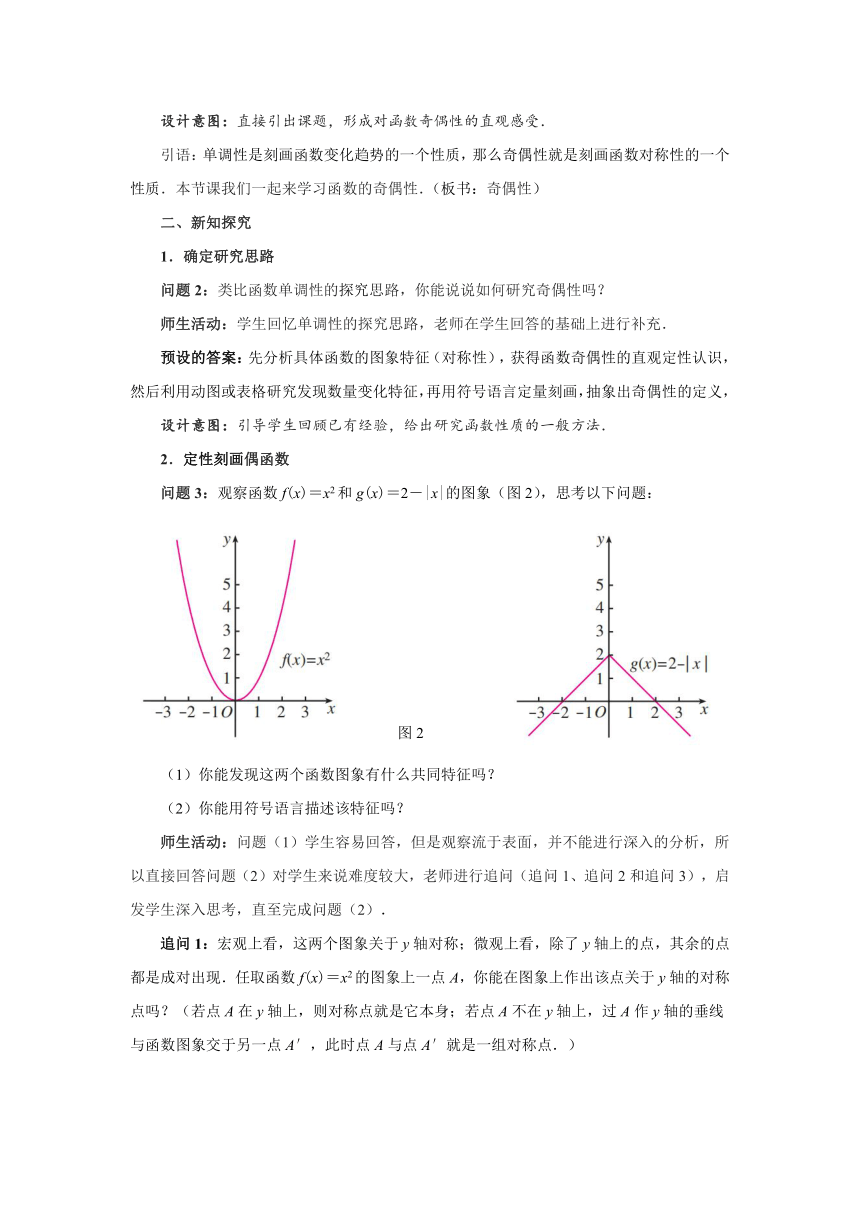
问题1:观察图1中的两个函数图象,你能发现它们的共同特征吗?
师生活动:学生观察容易发现这两个图象都有对称性,老师顺势引出课题.
预设的答案:图象的共同特征是它们都有对称性.
设计意图:直接引出课题,形成对函数奇偶性的直观感受.
引语:单调性是刻画函数变化趋势的一个性质,那么奇偶性就是刻画函数对称性的一个性质.本节课我们一起来学习函数的奇偶性.(板书:奇偶性)
二、新知探究
1.确定研究思路
问题2:类比函数单调性的探究思路,你能说说如何研究奇偶性吗?
师生活动:学生回忆单调性的探究思路,老师在学生回答的基础上进行补充.
预设的答案:先分析具体函数的图象特征(对称性),获得函数奇偶性的直观定性认识,然后利用动图或表格研究发现数量变化特征,再用符号语言定量刻画,抽象出奇偶性的定义,
设计意图:引导学生回顾已有经验,给出研究函数性质的一般方法.
2.定性刻画偶函数
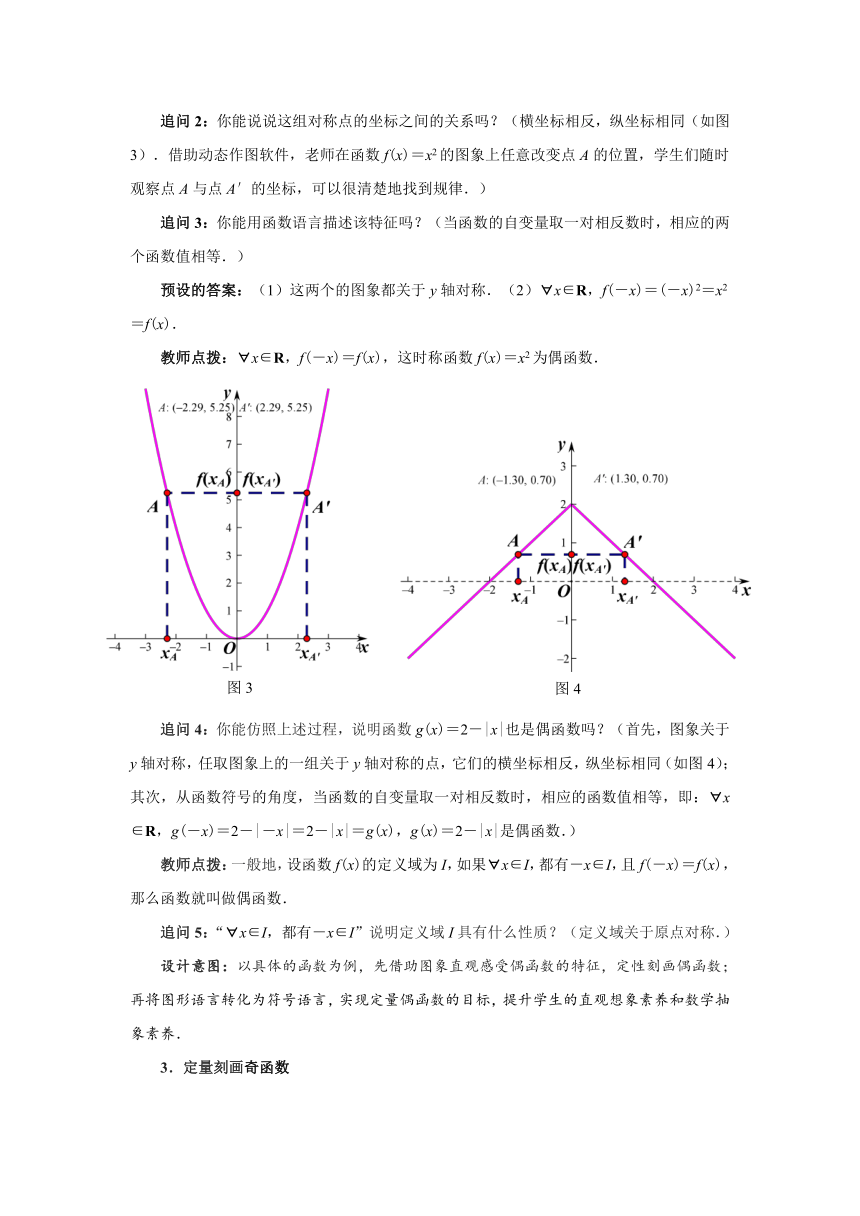
问题3:观察函数f(x)=x2和g(x)=2-|x|的图象(图2),思考以下问题:
(1)你能发现这两个函数图象有什么共同特征吗?
(2)你能用符号语言描述该特征吗?
师生活动:问题(1)学生容易回答,但是观察流于表面,并不能进行深入的分析,所以直接回答问题(2)对学生来说难度较大,老师进行追问(追问1、追问2和追问3),启发学生深入思考,直至完成问题(2).
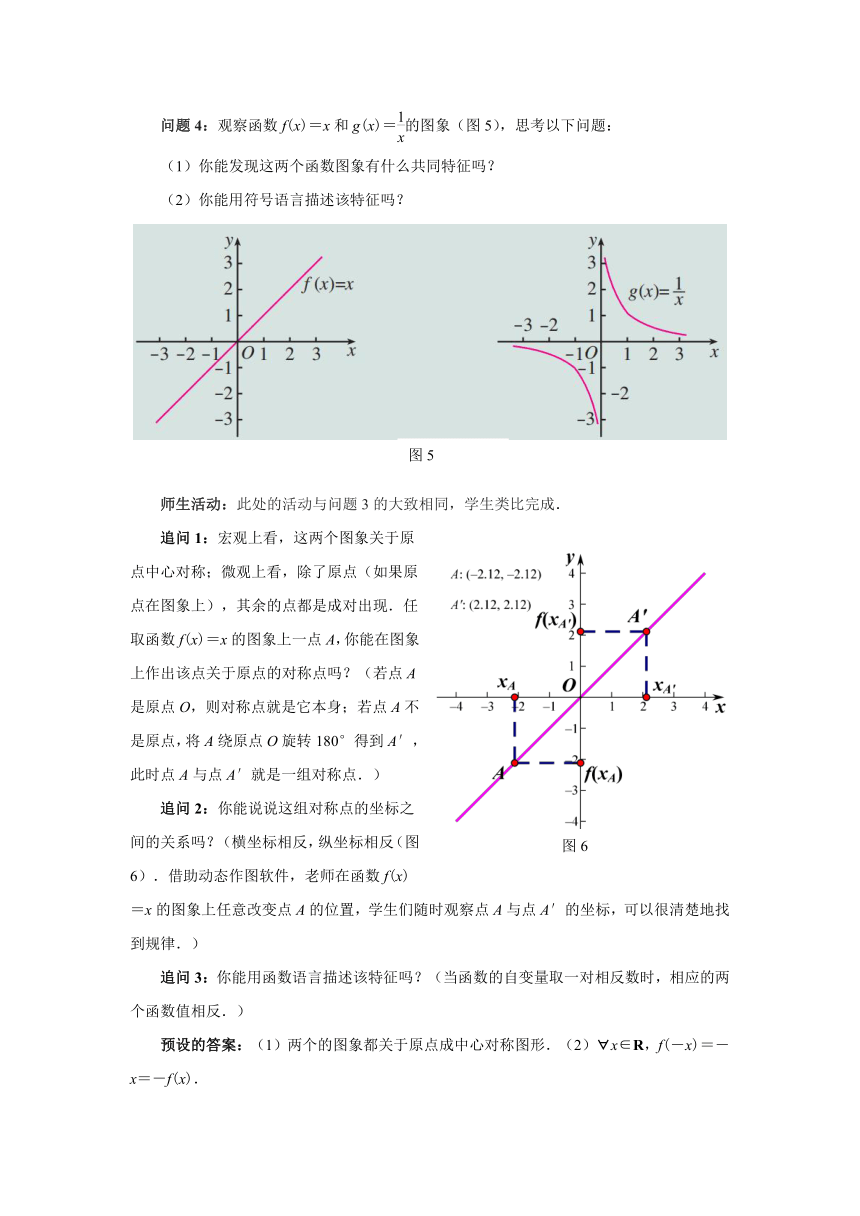
追问1:宏观上看,这两个图象关于y轴对称;微观上看,除了y轴上的点,其余的点都是成对出现.任取函数f(x)=x2的图象上一点A,你能在图象上作出该点关于y轴的对称点吗?(若点A在y轴上,则对称点就是它本身;若点A不在y轴上,过A作y轴的垂线与函数图象交于另一点A′,此时点A与点A′就是一组对称点.)
追问2:你能说说这组对称点的坐标之间的关系吗?(横坐标相反,纵坐标相同(如图3).借助动态作图软件,老师在函数f(x)=x2的图象上任意改变点A的位置,学生们随时观察点A与点A′的坐标,可以很清楚地找到规律.)
追问3:你能用函数语言描述该特征吗?(当函数的自变量取一对相反数时,相应的两个函数值相等.)
预设的答案:(1)这两个的图象都关于y轴对称.(2)?x∈R,f(-x)=(-x)2=x2=f(x).
教师点拨:?x∈R,f(-x)=f(x),这时称函数f(x)=x2为偶函数.
追问4:你能仿照上述过程,说明函数g(x)=2-|x|也是偶函数吗?(首先,图象关于y轴对称,任取图象上的一组关于y轴对称的点,它们的横坐标相反,纵坐标相同(如图4);其次,从函数符号的角度,当函数的自变量取一对相反数时,相应的函数值相等,即:?x∈R,g(-x)=2-|-x|=2-|x|=g(x),g(x)=2-|x|是偶函数.)
教师点拨:一般地,设函数f(x)的定义域为I,如果?x∈I,都有-x∈I,且f(-x)=f(x),那么函数就叫做偶函数.
追问5:“?x∈I,都有-x∈I”说明定义域I具有什么性质?(定义域关于原点对称.)
设计意图:以具体的函数为例,先借助图象直观感受偶函数的特征,定性刻画偶函数;再将图形语言转化为符号语言,实现定量偶函数的目标,提升学生的直观想象素养和数学抽象素养.
3.定量刻画奇函数
问题4:观察函数f(x)=x和g(x)=的图象(图5),思考以下问题:
(1)你能发现这两个函数图象有什么共同特征吗?
(2)你能用符号语言描述该特征吗?
师生活动:此处的活动与问题3的大致相同,学生类比完成.
追问1:宏观上看,这两个图象关于原点中心对称;微观上看,除了原点(如果原点在图象上),其余的点都是成对出现.任取函数f(x)=x的图象上一点A,你能在图象上作出该点关于原点的对称点吗?(若点A是原点O,则对称点就是它本身;若点A不是原点,将A绕原点O旋转180°得到A′,此时点A与点A′就是一组对称点.)
追问2:你能说说这组对称点的坐标之间的关系吗?(横坐标相反,纵坐标相反(图6).借助动态作图软件,老师在函数f(x)=x的图象上任意改变点A的位置,学生们随时观察点A与点A′的坐标,可以很清楚地找到规律.)
追问3:你能用函数语言描述该特征吗?(当函数的自变量取一对相反数时,相应的两个函数值相反.)
预设的答案:(1)两个的图象都关于原点成中心对称图形.(2)?x∈R,f(-x)=-x=-f(x).
教师点拨:?x∈R,f(-x)=-f(x),这时称函数f(x)=x为奇函数.
追问4:你能仿照上述过程,说明函数g(x)=也是奇函数吗?(首先,图象关于原点中心对称,任取图象上的一组关于原点轴对称的点,它们的横坐标相反,纵坐标也相反(图7);其次,从函数符号的角度,当函数的自变量取一对相反数时,相应的函数值相反,即:?x∈(-∞,0)∪(0,+∞),g(-x)==-=-g(x),函数g(x)=是奇函数.)
教师点拨:一般地,设函数f(x)的定义域为I,如果?x∈I,都有-x∈I,且f(-x)=-f(x),那么函数就叫做奇函数.
设计意图:类比定量刻画偶函数的过程,不仅得到奇函数的定量刻画,而且能熟悉研究函数性质的路径与方法.
4.奇偶性的判定
例1 判断下列函数的奇偶性:
(1)f(x)=x4; (2)f(x)=x5;
(3)f(x)=x+; (4)f(x)=.
师生活动:老师引导学生寻找判定的依据——定义,根据定义,求出函数的定义域I后,需要判断两个条件:(1)?x∈I,-x是否属于I;(2)f(-x)=f(x)或f(-x)=-f(x)是否成立,只有(1)、(2)同时成立,才能判断函数的奇偶性.
预设的答案:
解:(1)函数f(x)=x4的定义域为R.
?x∈R,都有-x∈R,且f(-x)=(-x)4=x4=f(x) ,
函数f(x)=x4为偶函数.
(2)函数f(x)=x5定义域为R.
?x∈R,都有-x∈R,且f(-x)=(-x)5=-x5=-f(x) ,
函数f(x)=x5为奇函数.
(3)函数f(x)=x+的定义域为(-∞,0)∪(0,+∞).
?x∈(-∞,0)∪(0,+∞),都有-x∈(-∞,0)∪(0,+∞),
且f(-x)=-x+=-(x+)=-f(x) ,
函数f(x)=x+为奇函数.
(4)函数f(x)=的定义域为(-∞,0)∪(0,+∞).
?x∈(-∞,0)∪(0,+∞),都有-x∈(-∞,0)∪(0,+∞),
且f(-x)===f(x) ,
函数f(x)=为偶函数.
追问1:你能总结用定义法判断奇偶性的步骤吗?(第一步,求函数的定义域I.第二步,判断定义域是否关于原点对称.若否,则函数不具有奇偶性,结束判断;若是,则进行第三步.第三步,?x∈I,计算f(-x).若f(-x)=f(x),则为偶函数;若f(-x)=-f(x),则为奇函数;若f(-x)与f(x)既不相等也不相反,则既不是奇函数也不是偶函数.)
追问2:思考
(1)判断函数f(x)=x3+x的奇偶性.
(2)图8是函数f(x)=x3+x图象的一部分,你能根据f(x)的奇偶性画出它在y轴左边的图象吗?
(3)一般地,如果知道y=f(x)为偶(奇)函数,那么我们可以怎样简化对它的研究?
((1)?x∈R,都有-x∈R,且f(-x)=(-x)3+(-x)=-(x3+x)=-f(x) ,函数f(x)=x3+x为奇函数.
(2)因为是奇函数,所以图象关于原点中心对称,我们可以先将图象沿着y轴翻折,再沿着x轴翻折就可以得到y轴左边的图象(图9).
(3)一般我们只需要研究y轴一侧的性质,然后根据对称性推断得到它在整个定义域内的性质.)
设计意图:例1和追问1帮助学生掌握应用定义判定奇偶性的程序,进一步加深对概念的认识,在证明过程中提升学生的逻辑推理素养和数学运算素养.追问2让学生利用函数的奇偶性画函数的图象,体会奇偶性对于研究函数性质时的简化作用,提升学生的直观想象素养.
三、归纳小结,布置作业
问题5:回忆本节课的内容,请你回答以下几个问题:
(1)什么是奇(偶)函数?用定义判定奇偶性的步骤是怎样的?
(2)请你比较奇函数的定义与偶函数的定义,说说这两者的异同.
师生活动:师生一起总结.
预设的答案:(1)概念和步骤略;
(2)相同点:①定义域关于原点对称;②都是函数的整体性质.不同点:①偶函数的图象关于y轴对称,而奇函数的图象关于原点对称;②当自变量取一对相反数时,偶函数的函数值相同,而奇函数的函数值相反.
设计意图:通过梳理本节课的内容,让学生更加明确函数奇偶性的内涵和判定.
作业布置:教科书习题3.2第5,11,12,13题.
四、目标检测设计
1.已知f(x)是偶函数,g(x)是奇函数,试将下图补充完整.
设计意图:训练学生根据奇偶性补全函数图象的能力,考查奇偶性的定义.
2.判断下列函数的奇偶性:
(1)f(x)=2x4+3x2; (2)f(x)=x3-2x .
设计意图:考查奇偶性的定义.
3.(1)从偶函数的定义出发,证明函数y=f(x)是偶函数的充要条件是它的图象关于y轴对称;
(2)从奇函数的定义出发,证明函数y=f(x)是奇函数的充要条件是它的图象关于原点对称 .
设计意图:通过证明符号语言与图象语言的等价性,深化理解奇偶性的定义.
参考答案:
1.略.
2.(1)偶函数.(2)奇函数.
3.(1)充分性:设P(x,y)是函数f(x)图象上任意一点,则y=f(x).因为函数f(x)的图象关于y轴对称,所以点P关于y轴的对称点Q(-x,y)也在函数f(x)图象上,即y=f(-x),所以对任意的x,都有f(-x)=f(x),所以函数是偶函数.
必要性:设P(x,y)是函数f(x)图象上任意一点,则y=f(x).记点P关于y轴对称点为Q,则Q(-x,y).因为函数f(x)是偶函数,所以f(-x)=f(x),即y=f(-x),所以点Q在函数图象上,所以函数f(x)的图象关于y轴对称.
(2)类比(1)中的证明过程可证.
教学目标
1.能类比单调性的探究思路,抽象出函数奇偶性的定义,提升学生的直观想象素养和数学抽象素养;了解奇函数与偶函数的定义和图象特征,能从函数图象直观判断函数是否具有奇偶性.
2.能根据函数奇偶性的定义判断函数的奇偶性;能利用函数的奇偶性帮助画函数图象和计算函数值,提升学生的逻辑推理和数学运算素养.
教学重难点
教学重点:了解奇函数与偶函数的定义和图象特征,根据函数奇偶性的定义判断函数的奇偶性.
教学难点:“图象关于y轴(原点)对称”转化为定量的符号语言.
课前准备
用软件制作动画;PPT课件.
教学过程
一、问题导入
问题1:观察图1中的两个函数图象,你能发现它们的共同特征吗?
师生活动:学生观察容易发现这两个图象都有对称性,老师顺势引出课题.
预设的答案:图象的共同特征是它们都有对称性.
设计意图:直接引出课题,形成对函数奇偶性的直观感受.
引语:单调性是刻画函数变化趋势的一个性质,那么奇偶性就是刻画函数对称性的一个性质.本节课我们一起来学习函数的奇偶性.(板书:奇偶性)
二、新知探究
1.确定研究思路
问题2:类比函数单调性的探究思路,你能说说如何研究奇偶性吗?
师生活动:学生回忆单调性的探究思路,老师在学生回答的基础上进行补充.
预设的答案:先分析具体函数的图象特征(对称性),获得函数奇偶性的直观定性认识,然后利用动图或表格研究发现数量变化特征,再用符号语言定量刻画,抽象出奇偶性的定义,
设计意图:引导学生回顾已有经验,给出研究函数性质的一般方法.
2.定性刻画偶函数
问题3:观察函数f(x)=x2和g(x)=2-|x|的图象(图2),思考以下问题:
(1)你能发现这两个函数图象有什么共同特征吗?
(2)你能用符号语言描述该特征吗?
师生活动:问题(1)学生容易回答,但是观察流于表面,并不能进行深入的分析,所以直接回答问题(2)对学生来说难度较大,老师进行追问(追问1、追问2和追问3),启发学生深入思考,直至完成问题(2).
追问1:宏观上看,这两个图象关于y轴对称;微观上看,除了y轴上的点,其余的点都是成对出现.任取函数f(x)=x2的图象上一点A,你能在图象上作出该点关于y轴的对称点吗?(若点A在y轴上,则对称点就是它本身;若点A不在y轴上,过A作y轴的垂线与函数图象交于另一点A′,此时点A与点A′就是一组对称点.)
追问2:你能说说这组对称点的坐标之间的关系吗?(横坐标相反,纵坐标相同(如图3).借助动态作图软件,老师在函数f(x)=x2的图象上任意改变点A的位置,学生们随时观察点A与点A′的坐标,可以很清楚地找到规律.)
追问3:你能用函数语言描述该特征吗?(当函数的自变量取一对相反数时,相应的两个函数值相等.)
预设的答案:(1)这两个的图象都关于y轴对称.(2)?x∈R,f(-x)=(-x)2=x2=f(x).
教师点拨:?x∈R,f(-x)=f(x),这时称函数f(x)=x2为偶函数.
追问4:你能仿照上述过程,说明函数g(x)=2-|x|也是偶函数吗?(首先,图象关于y轴对称,任取图象上的一组关于y轴对称的点,它们的横坐标相反,纵坐标相同(如图4);其次,从函数符号的角度,当函数的自变量取一对相反数时,相应的函数值相等,即:?x∈R,g(-x)=2-|-x|=2-|x|=g(x),g(x)=2-|x|是偶函数.)
教师点拨:一般地,设函数f(x)的定义域为I,如果?x∈I,都有-x∈I,且f(-x)=f(x),那么函数就叫做偶函数.
追问5:“?x∈I,都有-x∈I”说明定义域I具有什么性质?(定义域关于原点对称.)
设计意图:以具体的函数为例,先借助图象直观感受偶函数的特征,定性刻画偶函数;再将图形语言转化为符号语言,实现定量偶函数的目标,提升学生的直观想象素养和数学抽象素养.
3.定量刻画奇函数
问题4:观察函数f(x)=x和g(x)=的图象(图5),思考以下问题:
(1)你能发现这两个函数图象有什么共同特征吗?
(2)你能用符号语言描述该特征吗?
师生活动:此处的活动与问题3的大致相同,学生类比完成.
追问1:宏观上看,这两个图象关于原点中心对称;微观上看,除了原点(如果原点在图象上),其余的点都是成对出现.任取函数f(x)=x的图象上一点A,你能在图象上作出该点关于原点的对称点吗?(若点A是原点O,则对称点就是它本身;若点A不是原点,将A绕原点O旋转180°得到A′,此时点A与点A′就是一组对称点.)
追问2:你能说说这组对称点的坐标之间的关系吗?(横坐标相反,纵坐标相反(图6).借助动态作图软件,老师在函数f(x)=x的图象上任意改变点A的位置,学生们随时观察点A与点A′的坐标,可以很清楚地找到规律.)
追问3:你能用函数语言描述该特征吗?(当函数的自变量取一对相反数时,相应的两个函数值相反.)
预设的答案:(1)两个的图象都关于原点成中心对称图形.(2)?x∈R,f(-x)=-x=-f(x).
教师点拨:?x∈R,f(-x)=-f(x),这时称函数f(x)=x为奇函数.
追问4:你能仿照上述过程,说明函数g(x)=也是奇函数吗?(首先,图象关于原点中心对称,任取图象上的一组关于原点轴对称的点,它们的横坐标相反,纵坐标也相反(图7);其次,从函数符号的角度,当函数的自变量取一对相反数时,相应的函数值相反,即:?x∈(-∞,0)∪(0,+∞),g(-x)==-=-g(x),函数g(x)=是奇函数.)
教师点拨:一般地,设函数f(x)的定义域为I,如果?x∈I,都有-x∈I,且f(-x)=-f(x),那么函数就叫做奇函数.
设计意图:类比定量刻画偶函数的过程,不仅得到奇函数的定量刻画,而且能熟悉研究函数性质的路径与方法.
4.奇偶性的判定
例1 判断下列函数的奇偶性:
(1)f(x)=x4; (2)f(x)=x5;
(3)f(x)=x+; (4)f(x)=.
师生活动:老师引导学生寻找判定的依据——定义,根据定义,求出函数的定义域I后,需要判断两个条件:(1)?x∈I,-x是否属于I;(2)f(-x)=f(x)或f(-x)=-f(x)是否成立,只有(1)、(2)同时成立,才能判断函数的奇偶性.
预设的答案:
解:(1)函数f(x)=x4的定义域为R.
?x∈R,都有-x∈R,且f(-x)=(-x)4=x4=f(x) ,
函数f(x)=x4为偶函数.
(2)函数f(x)=x5定义域为R.
?x∈R,都有-x∈R,且f(-x)=(-x)5=-x5=-f(x) ,
函数f(x)=x5为奇函数.
(3)函数f(x)=x+的定义域为(-∞,0)∪(0,+∞).
?x∈(-∞,0)∪(0,+∞),都有-x∈(-∞,0)∪(0,+∞),
且f(-x)=-x+=-(x+)=-f(x) ,
函数f(x)=x+为奇函数.
(4)函数f(x)=的定义域为(-∞,0)∪(0,+∞).
?x∈(-∞,0)∪(0,+∞),都有-x∈(-∞,0)∪(0,+∞),
且f(-x)===f(x) ,
函数f(x)=为偶函数.
追问1:你能总结用定义法判断奇偶性的步骤吗?(第一步,求函数的定义域I.第二步,判断定义域是否关于原点对称.若否,则函数不具有奇偶性,结束判断;若是,则进行第三步.第三步,?x∈I,计算f(-x).若f(-x)=f(x),则为偶函数;若f(-x)=-f(x),则为奇函数;若f(-x)与f(x)既不相等也不相反,则既不是奇函数也不是偶函数.)
追问2:思考
(1)判断函数f(x)=x3+x的奇偶性.
(2)图8是函数f(x)=x3+x图象的一部分,你能根据f(x)的奇偶性画出它在y轴左边的图象吗?
(3)一般地,如果知道y=f(x)为偶(奇)函数,那么我们可以怎样简化对它的研究?
((1)?x∈R,都有-x∈R,且f(-x)=(-x)3+(-x)=-(x3+x)=-f(x) ,函数f(x)=x3+x为奇函数.
(2)因为是奇函数,所以图象关于原点中心对称,我们可以先将图象沿着y轴翻折,再沿着x轴翻折就可以得到y轴左边的图象(图9).
(3)一般我们只需要研究y轴一侧的性质,然后根据对称性推断得到它在整个定义域内的性质.)
设计意图:例1和追问1帮助学生掌握应用定义判定奇偶性的程序,进一步加深对概念的认识,在证明过程中提升学生的逻辑推理素养和数学运算素养.追问2让学生利用函数的奇偶性画函数的图象,体会奇偶性对于研究函数性质时的简化作用,提升学生的直观想象素养.
三、归纳小结,布置作业
问题5:回忆本节课的内容,请你回答以下几个问题:
(1)什么是奇(偶)函数?用定义判定奇偶性的步骤是怎样的?
(2)请你比较奇函数的定义与偶函数的定义,说说这两者的异同.
师生活动:师生一起总结.
预设的答案:(1)概念和步骤略;
(2)相同点:①定义域关于原点对称;②都是函数的整体性质.不同点:①偶函数的图象关于y轴对称,而奇函数的图象关于原点对称;②当自变量取一对相反数时,偶函数的函数值相同,而奇函数的函数值相反.
设计意图:通过梳理本节课的内容,让学生更加明确函数奇偶性的内涵和判定.
作业布置:教科书习题3.2第5,11,12,13题.
四、目标检测设计
1.已知f(x)是偶函数,g(x)是奇函数,试将下图补充完整.
设计意图:训练学生根据奇偶性补全函数图象的能力,考查奇偶性的定义.
2.判断下列函数的奇偶性:
(1)f(x)=2x4+3x2; (2)f(x)=x3-2x .
设计意图:考查奇偶性的定义.
3.(1)从偶函数的定义出发,证明函数y=f(x)是偶函数的充要条件是它的图象关于y轴对称;
(2)从奇函数的定义出发,证明函数y=f(x)是奇函数的充要条件是它的图象关于原点对称 .
设计意图:通过证明符号语言与图象语言的等价性,深化理解奇偶性的定义.
参考答案:
1.略.
2.(1)偶函数.(2)奇函数.
3.(1)充分性:设P(x,y)是函数f(x)图象上任意一点,则y=f(x).因为函数f(x)的图象关于y轴对称,所以点P关于y轴的对称点Q(-x,y)也在函数f(x)图象上,即y=f(-x),所以对任意的x,都有f(-x)=f(x),所以函数是偶函数.
必要性:设P(x,y)是函数f(x)图象上任意一点,则y=f(x).记点P关于y轴对称点为Q,则Q(-x,y).因为函数f(x)是偶函数,所以f(-x)=f(x),即y=f(-x),所以点Q在函数图象上,所以函数f(x)的图象关于y轴对称.
(2)类比(1)中的证明过程可证.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
