人教版数学七年级上册习题课件:4.4课题学习 设计制作长方体形状的包装纸盒(22张ppt)
文档属性
| 名称 | 人教版数学七年级上册习题课件:4.4课题学习 设计制作长方体形状的包装纸盒(22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-08 00:00:00 | ||
图片预览






文档简介
第四章 几何图形初步
4.4 课题学习 设计制作长方体形状的包装纸盒
1.柱体的展开图
(1)长方体共有_____个面.
(2)将一个圆柱的侧面剪开得到一个长方形,其中圆柱的底面________等于长方形的一条边长,长方形的另一边长等于____________.
6
周长
圆柱的高
2.制作长方体形状的包装盒
(1)观察、讨论;
(2)设计、制作;
(3)交流、比较;
(4)评价、小结;
(5)巩固、提高.
1.长方体纸盒的长、宽、高分别是10 cm,8 cm,5 cm,若将它沿棱剪开,展成一个平面图形,那么这个平面图形的周长的最小值是多少?
【答案】这个平面图形的周长的最小值是5×8+8×4+10×2=92(cm).
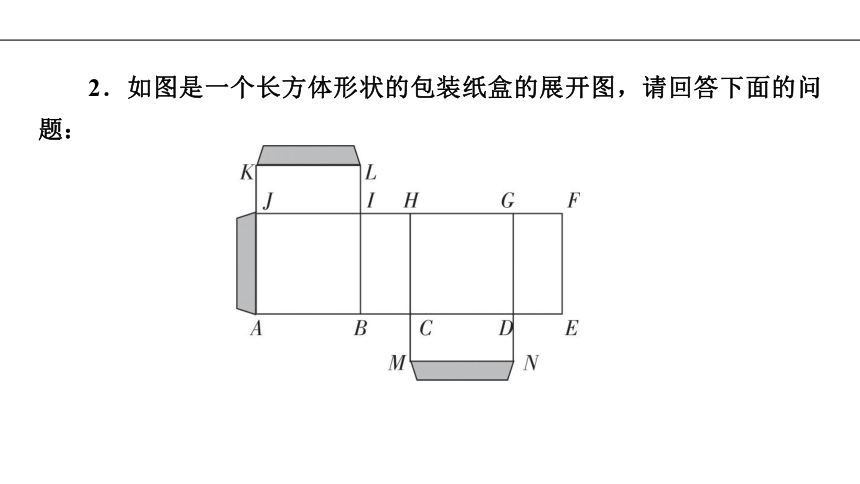
2.如图是一个长方体形状的包装纸盒的展开图,请回答下面的问题:
(1)A点的对应点(指把展开图折叠成长方体后能重合在一起的点)是__________,B点的对应点是______,F点的对应点是______,G点的对应点是______,H点的对应点是______.
(2)如果AB=80 mm,AJ=75 mm,BC=40 mm,则GH=______mm,DN=______mm,EF=______mm.
E和N
M
J
K
L
80
40
75
知识点1 长方体的折叠与展开
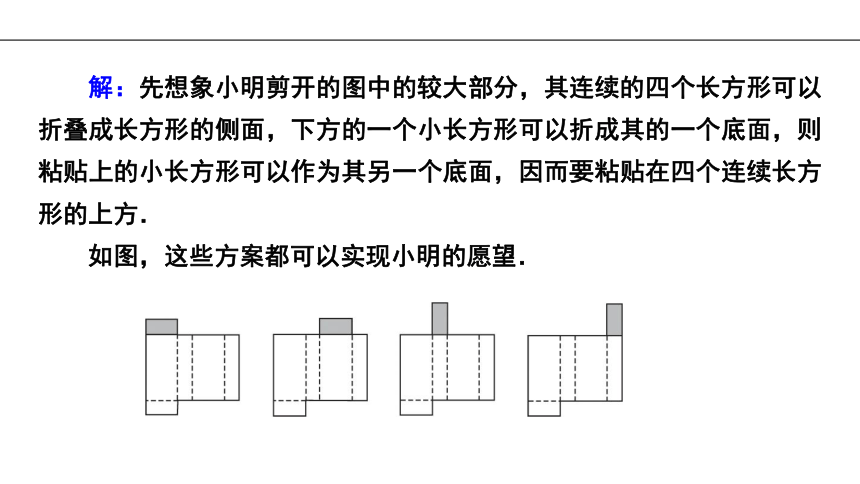
例1 小明在把一个长方体纸盒展开时,不小心多剪了一刀,结果展开后变成了两部分,如图所示,现在他想把这两部分粘贴成一个整体,使之能折成原来的长方体,请你帮他策划一下,该怎样粘贴?
解:先想象小明剪开的图中的较大部分,其连续的四个长方形可以折叠成长方形的侧面,下方的一个小长方形可以折成其的一个底面,则粘贴上的小长方形可以作为其另一个底面,因而要粘贴在四个连续长方形的上方.
如图,这些方案都可以实现小明的愿望.
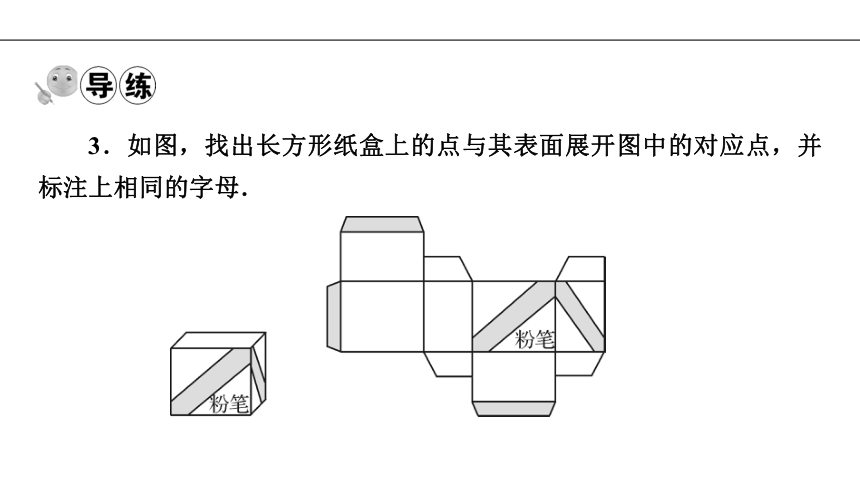
3.如图,找出长方形纸盒上的点与其表面展开图中的对应点,并标注上相同的字母.
解:可按如下的步骤进行操作:(1)把直观图中看不见的部分用虚线标出,并把直观图标上字母;(2)根据直观图和展开图中的图案,确定展开图中的对应面上的对应点,并标上相应的字母;(3)想象折叠或展开的过程,找出其他对应点并标上字母.
知识点2 折纸与剪纸问题
例2 将一张正方形纸片按图1、图2所示的方式依次对折后,再沿图3中的虚线剪裁,最后将图4中的纸片打开铺平,所得到的图案是 ( )
B
4.如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是 ( )
D
【第一关】
1.如图是一个长方体形状包装盒的表面展开图,包装材料厚度不计,折叠制作完成后得到长方体的容积是 ( )
A.40×40×70
B.40×70×80
C.70×80×80
D.80×80×80
B
2.将一圆形纸片对折后再对折,得到左下图,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是 ( )
C
3.将一个长方形纸片依次按图1、图2的方式对折,然后沿图3中的虚线裁剪,最后将图4的纸再展开铺平,所得到的图案是 ( )
A
【第二关】
4.如图是某些几何体的表面展开图,请填出这些几何体的名称.
圆锥
三棱柱
长方体
5.小明在硬纸上设计了一个长方体的纸盒,并已沿设计稿的轮廓把展开图剪下,如图所示,A,B,C,D,E,F将是长方体纸盒的6个面,1,2,3,4各部分是一种衬托,将和某个面叠合在一起,深色部分是预留的粘合处.
(1)折叠前还需要把三处剪开,这三处分别是面A和1的交界处,_________的交界处,_________的交界处;
(2)折叠后,1,2两部分将和面______叠合在一起,3,4两部分将和面______叠合在一起;
(3)如果B在前面,那么,______面将在后面;如果F面在下面,那么______面将在上面.
F和3
F和4
A
F
D
A
【第三关】
6.一个长方体包装盒展开图如下图(单位:cm):
(1)这个长方体的棱长总和是______cm;
(2)将这个长方体放在桌子上,当占取桌面面积最小时,它占桌面的面积是______cm2,这时长方体高是______cm;
(3)请计算这个长方体包装盒的表面积;
(4)忽略纸的厚度和接头,计算长方体包装盒的容积;
(5)贝贝认为这个长方体包装盒的表面积与体积相等,你认为呢?
88
24
12
解:(3)长方体包装盒的表面积=(12×4+4×6+12×6)×2=288(cm2).
(4)长方体包装盒的容积=12×4×6=288(cm3).
(5)长方体包装盒的表面积与体积单位不同,无法比较.
4.4 课题学习 设计制作长方体形状的包装纸盒
1.柱体的展开图
(1)长方体共有_____个面.
(2)将一个圆柱的侧面剪开得到一个长方形,其中圆柱的底面________等于长方形的一条边长,长方形的另一边长等于____________.
6
周长
圆柱的高
2.制作长方体形状的包装盒
(1)观察、讨论;
(2)设计、制作;
(3)交流、比较;
(4)评价、小结;
(5)巩固、提高.
1.长方体纸盒的长、宽、高分别是10 cm,8 cm,5 cm,若将它沿棱剪开,展成一个平面图形,那么这个平面图形的周长的最小值是多少?
【答案】这个平面图形的周长的最小值是5×8+8×4+10×2=92(cm).
2.如图是一个长方体形状的包装纸盒的展开图,请回答下面的问题:
(1)A点的对应点(指把展开图折叠成长方体后能重合在一起的点)是__________,B点的对应点是______,F点的对应点是______,G点的对应点是______,H点的对应点是______.
(2)如果AB=80 mm,AJ=75 mm,BC=40 mm,则GH=______mm,DN=______mm,EF=______mm.
E和N
M
J
K
L
80
40
75
知识点1 长方体的折叠与展开
例1 小明在把一个长方体纸盒展开时,不小心多剪了一刀,结果展开后变成了两部分,如图所示,现在他想把这两部分粘贴成一个整体,使之能折成原来的长方体,请你帮他策划一下,该怎样粘贴?
解:先想象小明剪开的图中的较大部分,其连续的四个长方形可以折叠成长方形的侧面,下方的一个小长方形可以折成其的一个底面,则粘贴上的小长方形可以作为其另一个底面,因而要粘贴在四个连续长方形的上方.
如图,这些方案都可以实现小明的愿望.
3.如图,找出长方形纸盒上的点与其表面展开图中的对应点,并标注上相同的字母.
解:可按如下的步骤进行操作:(1)把直观图中看不见的部分用虚线标出,并把直观图标上字母;(2)根据直观图和展开图中的图案,确定展开图中的对应面上的对应点,并标上相应的字母;(3)想象折叠或展开的过程,找出其他对应点并标上字母.
知识点2 折纸与剪纸问题
例2 将一张正方形纸片按图1、图2所示的方式依次对折后,再沿图3中的虚线剪裁,最后将图4中的纸片打开铺平,所得到的图案是 ( )
B
4.如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是 ( )
D
【第一关】
1.如图是一个长方体形状包装盒的表面展开图,包装材料厚度不计,折叠制作完成后得到长方体的容积是 ( )
A.40×40×70
B.40×70×80
C.70×80×80
D.80×80×80
B
2.将一圆形纸片对折后再对折,得到左下图,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是 ( )
C
3.将一个长方形纸片依次按图1、图2的方式对折,然后沿图3中的虚线裁剪,最后将图4的纸再展开铺平,所得到的图案是 ( )
A
【第二关】
4.如图是某些几何体的表面展开图,请填出这些几何体的名称.
圆锥
三棱柱
长方体
5.小明在硬纸上设计了一个长方体的纸盒,并已沿设计稿的轮廓把展开图剪下,如图所示,A,B,C,D,E,F将是长方体纸盒的6个面,1,2,3,4各部分是一种衬托,将和某个面叠合在一起,深色部分是预留的粘合处.
(1)折叠前还需要把三处剪开,这三处分别是面A和1的交界处,_________的交界处,_________的交界处;
(2)折叠后,1,2两部分将和面______叠合在一起,3,4两部分将和面______叠合在一起;
(3)如果B在前面,那么,______面将在后面;如果F面在下面,那么______面将在上面.
F和3
F和4
A
F
D
A
【第三关】
6.一个长方体包装盒展开图如下图(单位:cm):
(1)这个长方体的棱长总和是______cm;
(2)将这个长方体放在桌子上,当占取桌面面积最小时,它占桌面的面积是______cm2,这时长方体高是______cm;
(3)请计算这个长方体包装盒的表面积;
(4)忽略纸的厚度和接头,计算长方体包装盒的容积;
(5)贝贝认为这个长方体包装盒的表面积与体积相等,你认为呢?
88
24
12
解:(3)长方体包装盒的表面积=(12×4+4×6+12×6)×2=288(cm2).
(4)长方体包装盒的容积=12×4×6=288(cm3).
(5)长方体包装盒的表面积与体积单位不同,无法比较.
