新人教版八上十字相乘法分解因式
文档属性
| 名称 | 新人教版八上十字相乘法分解因式 |  | |
| 格式 | rar | ||
| 文件大小 | 300.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-24 12:34:08 | ||
图片预览

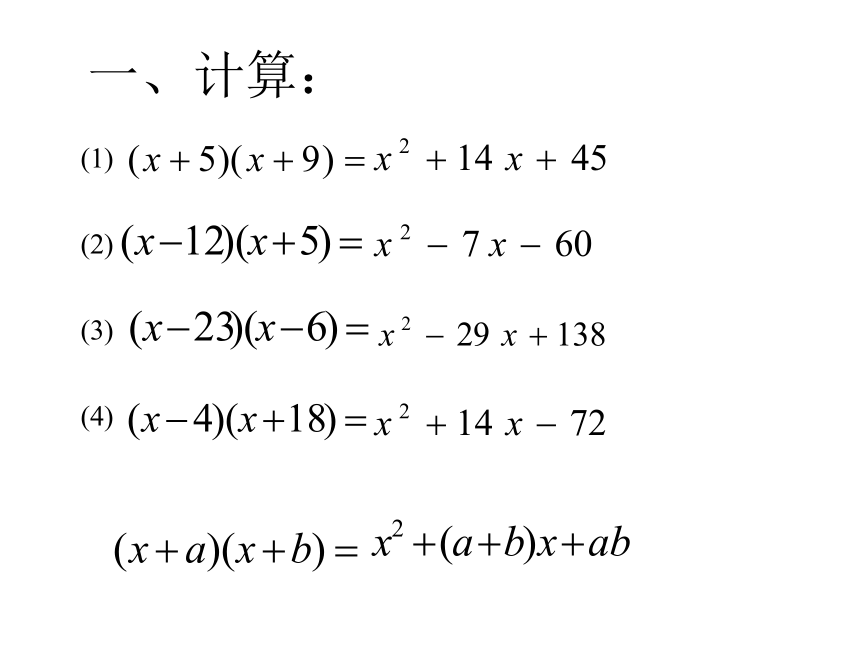

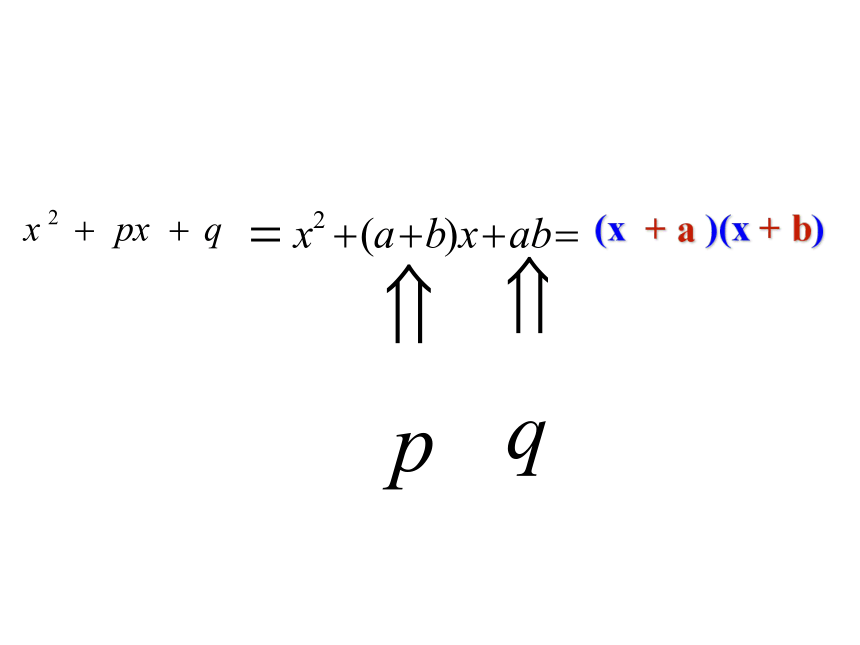





文档简介
(共23张PPT)
一、计算:
(1)
(2)
(3)
(4)
下列各式是因式分解吗?
(x + a )(x + b)
例一:
或
步骤:
①竖分二次项与常数项
②交叉相乘,和相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:竖分常数交叉验,
横写因式不能乱。
试一试:
小结:
用十字相乘法把形如
二次三项式分解因式使
(顺口溜:竖分常数交叉验,横写因式不能乱。)
练一练:
小结:
用十字相乘法把形如
二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )
同号
异号
将下列各式分解因式
观察:p与a、b符号关系
小结:
当q>0时,q分解的因数a、b( )
同号
异号
当q<0时, q分解的因数a、b( )
且(a、b符号)与p符号相同
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填 、 符号
=(x 3)(x 1)
=(x 3)(x 1)
=(y 4)(y 5)
=(t 4)(t 14)
+
+
-
+
-
-
-
+
当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同
1、十字相乘法
(借助十字交叉线分解因式的方法)
2、用十字相乘法把形如x2 + px +q 二次三项式分解因式
3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之间的符号关系
q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)
与p符号相同
本节总结
五、选择题:
以下多项式中分解因式为 的多项式是( )
A
B
C
D
c
试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
六、独立练习:把下列各式分解因式
1、含有x的二次三项式,其中x2系数是1,常数项为12,并能分解因式,这样的多项式共有几个?
若一次项的系数为整数,
则有6个;否则有无数个!!
2、分解因式
(1).x2+(a-1)x-a;
(2).(x+y) 2+8(x+y)-48;
(1)(x+a)(x-1)
(2)(x+y+12)(x+y-4)
十字相乘法分解因式(2)
本节课解决两个问题:
第一:对形如ax2+bx+c (a≠0)的二次三项式
进行因式分解;
第二:对形如ax2+bxy+cy2 (a≠0)的二次三项式
进行因式分解;
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1) (a2x+c2) =ax2+bx+c (a≠0)
ax2+bx+c=(a1x+c1) (a2x+c2) (a≠0)
整式运算
因式分解
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1y) (a2x+c2y) =ax2+bxy+cy2
ax2+bxy+cy2=(a1x+c1y) (a2x+c2y)
整式运算
因式分解
例1:2x2-7x+3
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
例2 分解因式 3x2 -10x+3
解:3x2 -10x+3
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
例3 分解因式 5x2-17xy-12y
解:5x2 -17xy-12y2
5x
x
+3y
-4y
-20x+3x=-17x
=(5x+3y)(x-4y)
例4 将 2(6x2 +x) 2-11(6x2 +x) +5 分解因式
解:2(6x2 +x)2-11(6x2 +x) +5
= [(6x2 +x) -5][2(6x2 +x)-1]
= (6x2 +x-5) (12x2 +2x-1 )
= (6x -5)(x +1) (12x2 +2x-1 )
1
2
-5
-1
-1-10=-11
6
1
-5
1
-5+6=1
练习:将下列各式分解因式
1、 7x -13x+6
2
3、 15x +7xy-4y
2
2
2、 -y -4y+12
2
答案(7x-6)(x-1)
4、 x -(a+1) x+a
2
答案- (y+6)(y-2)
答案 (3x-y)(5x+4y)
答案 (x-1)(x-a)
5、x2+11xy+10y2;
6、2x2-7xy+3y2;
7、-3a2+15ab-12b2;
8、
答案(x+10y)(x+y)
答案 (2x-y)(x-3y)
答案 -3(a-b)(a-4b)
答案 1/4(a-5b)(a+2b)
思考题
(1)(-x+5y)(3x-y)
(2)(2x-2y+1)(x-y-2)
一、计算:
(1)
(2)
(3)
(4)
下列各式是因式分解吗?
(x + a )(x + b)
例一:
或
步骤:
①竖分二次项与常数项
②交叉相乘,和相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:竖分常数交叉验,
横写因式不能乱。
试一试:
小结:
用十字相乘法把形如
二次三项式分解因式使
(顺口溜:竖分常数交叉验,横写因式不能乱。)
练一练:
小结:
用十字相乘法把形如
二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )
同号
异号
将下列各式分解因式
观察:p与a、b符号关系
小结:
当q>0时,q分解的因数a、b( )
同号
异号
当q<0时, q分解的因数a、b( )
且(a、b符号)与p符号相同
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填 、 符号
=(x 3)(x 1)
=(x 3)(x 1)
=(y 4)(y 5)
=(t 4)(t 14)
+
+
-
+
-
-
-
+
当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同
1、十字相乘法
(借助十字交叉线分解因式的方法)
2、用十字相乘法把形如x2 + px +q 二次三项式分解因式
3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之间的符号关系
q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)
与p符号相同
本节总结
五、选择题:
以下多项式中分解因式为 的多项式是( )
A
B
C
D
c
试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
六、独立练习:把下列各式分解因式
1、含有x的二次三项式,其中x2系数是1,常数项为12,并能分解因式,这样的多项式共有几个?
若一次项的系数为整数,
则有6个;否则有无数个!!
2、分解因式
(1).x2+(a-1)x-a;
(2).(x+y) 2+8(x+y)-48;
(1)(x+a)(x-1)
(2)(x+y+12)(x+y-4)
十字相乘法分解因式(2)
本节课解决两个问题:
第一:对形如ax2+bx+c (a≠0)的二次三项式
进行因式分解;
第二:对形如ax2+bxy+cy2 (a≠0)的二次三项式
进行因式分解;
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1) (a2x+c2) =ax2+bx+c (a≠0)
ax2+bx+c=(a1x+c1) (a2x+c2) (a≠0)
整式运算
因式分解
a2
c1
c2
a1c2+a2c1=b
a1
(a1x+c1y) (a2x+c2y) =ax2+bxy+cy2
ax2+bxy+cy2=(a1x+c1y) (a2x+c2y)
整式运算
因式分解
例1:2x2-7x+3
总结:
1、由常数项的符号确定分解的两数的符号
2、由一次项系数确定分解的方向
3、勿忘检验分解的合理性
例2 分解因式 3x2 -10x+3
解:3x2 -10x+3
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
例3 分解因式 5x2-17xy-12y
解:5x2 -17xy-12y2
5x
x
+3y
-4y
-20x+3x=-17x
=(5x+3y)(x-4y)
例4 将 2(6x2 +x) 2-11(6x2 +x) +5 分解因式
解:2(6x2 +x)2-11(6x2 +x) +5
= [(6x2 +x) -5][2(6x2 +x)-1]
= (6x2 +x-5) (12x2 +2x-1 )
= (6x -5)(x +1) (12x2 +2x-1 )
1
2
-5
-1
-1-10=-11
6
1
-5
1
-5+6=1
练习:将下列各式分解因式
1、 7x -13x+6
2
3、 15x +7xy-4y
2
2
2、 -y -4y+12
2
答案(7x-6)(x-1)
4、 x -(a+1) x+a
2
答案- (y+6)(y-2)
答案 (3x-y)(5x+4y)
答案 (x-1)(x-a)
5、x2+11xy+10y2;
6、2x2-7xy+3y2;
7、-3a2+15ab-12b2;
8、
答案(x+10y)(x+y)
答案 (2x-y)(x-3y)
答案 -3(a-b)(a-4b)
答案 1/4(a-5b)(a+2b)
思考题
(1)(-x+5y)(3x-y)
(2)(2x-2y+1)(x-y-2)
