《2.1、探索勾股定理》
图片预览


文档简介
(共21张PPT)
探索勾股定理
1
十二中 陈伟利
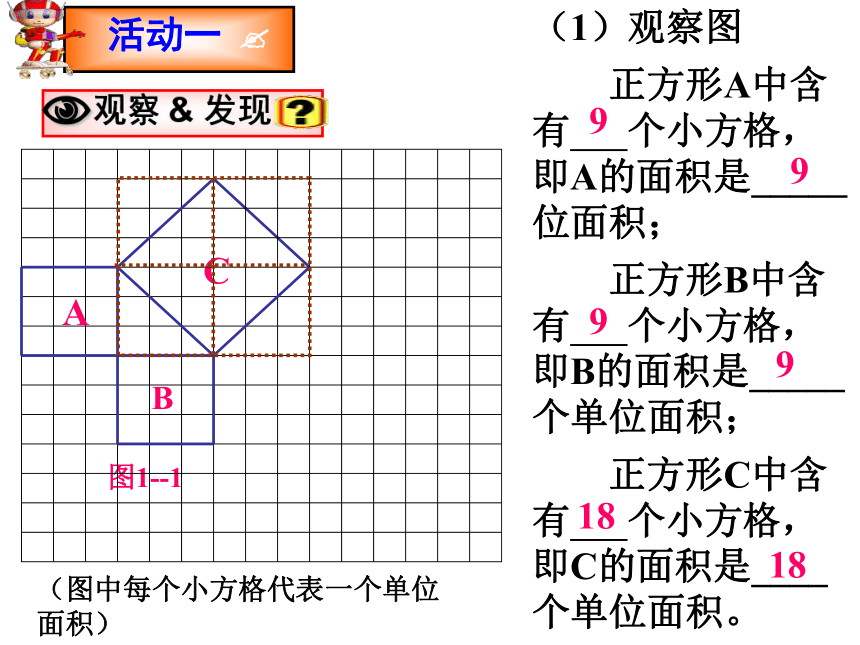
B
C
图1--1
A
(图中每个小方格代表一个单位面积)
(1)观察图
正方形A中含有 个小方格,即A的面积是_____位面积;
正方形B中含有 个小方格,即B的面积是_____个单位面积;
正方形C中含有 个小方格,即C的面积是____个单位面积。
9
9
18
9
9
18
观察 & 发现
活动一
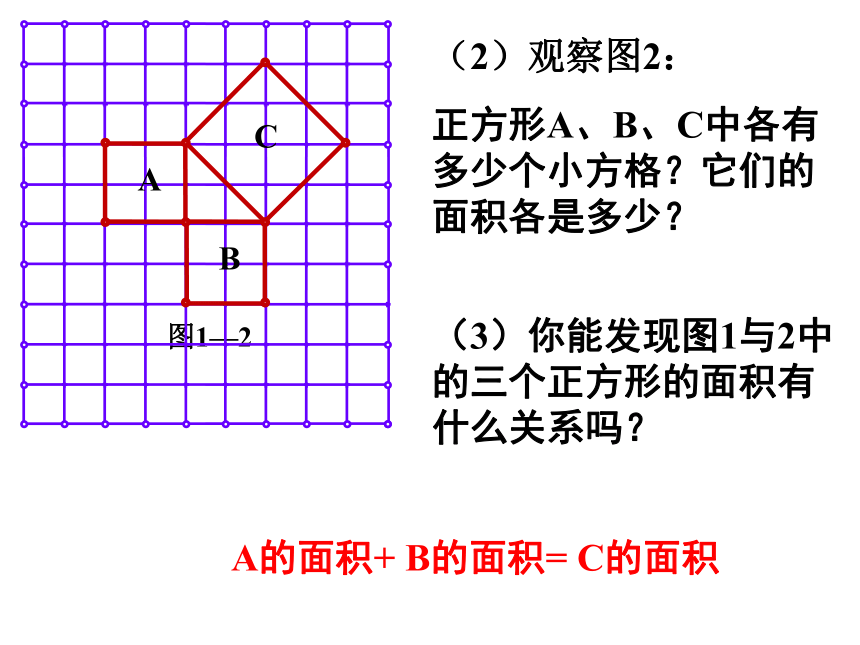
图1—2
A
B
C
(2)观察图2:
正方形A、B、C中各有多少个小方格?它们的面积各是多少?
A的面积+ B的面积= C的面积
(3)你能发现图1与2中的三个正方形的面积有什么关系吗?
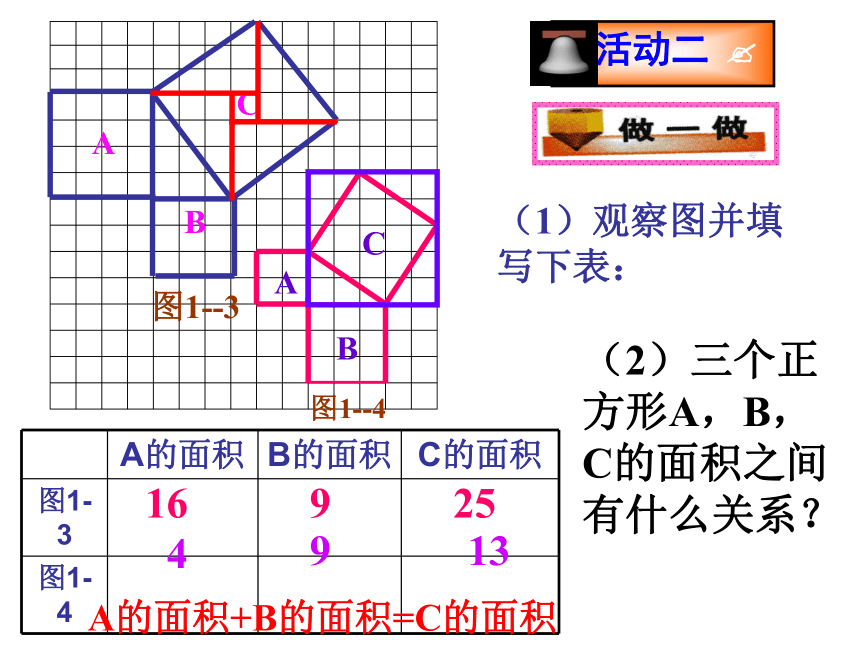
(1)观察图并填写下表:
A的面积 B的面积 C的面积
图1-3
图1-4
(2)三个正方形A,B,C的面积之间有什么关系?
16
9
25
4
9
13
A
B
C
图1--4
A
B
C
图1--3
A的面积+B的面积=C的面积
活动二
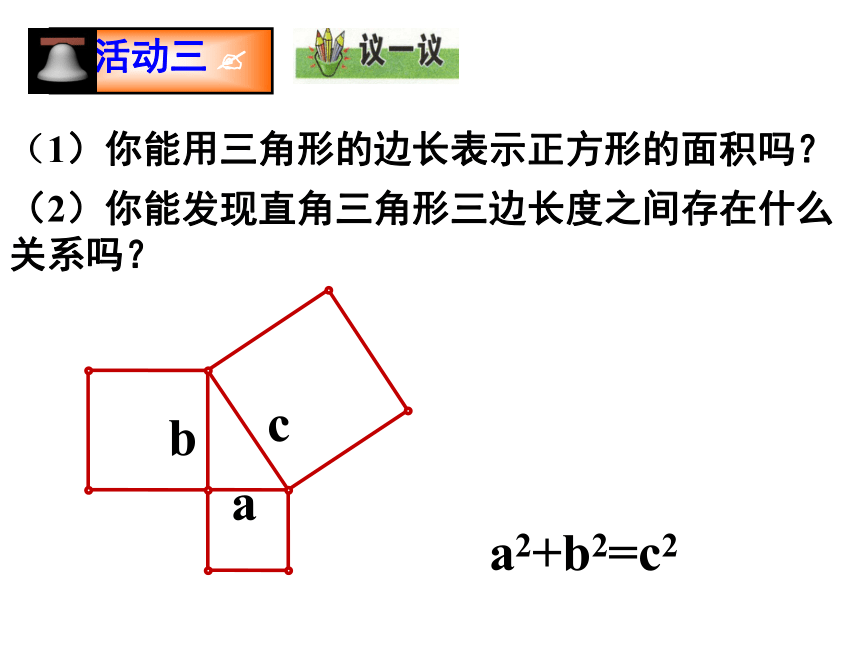
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
b
a
c
a2+b2=c2
活动三
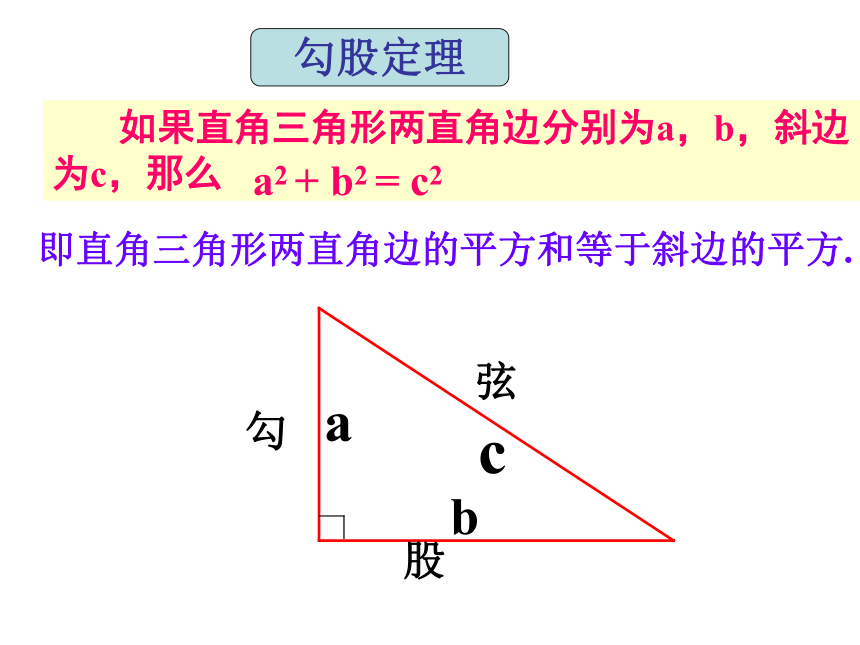
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理
c
a
b
勾
股
弦
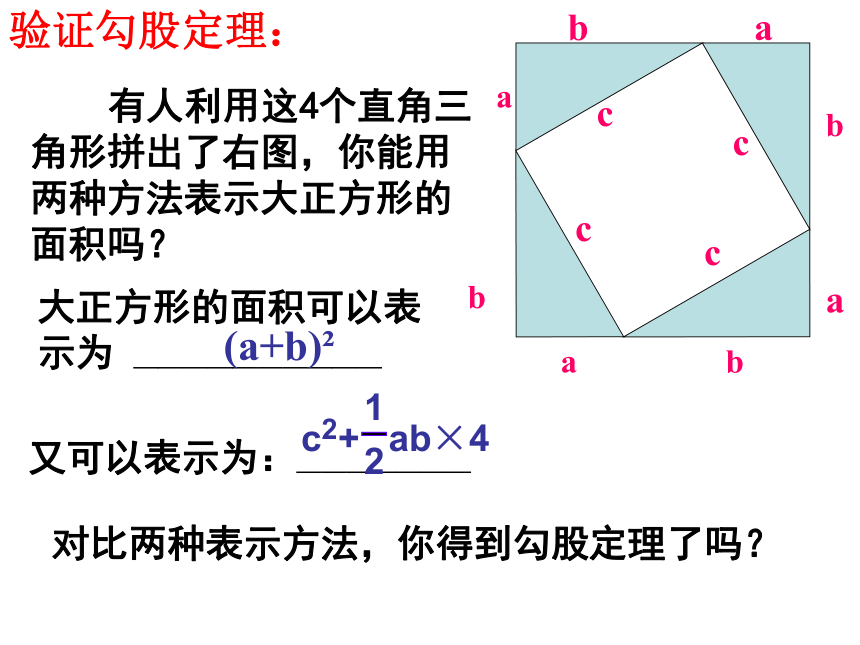
有人利用这4个直角三角形拼出了右图,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为 ——————————
又可以表示为:———————
a
a
a
a
b
b
b
b
c
c
c
c
对比两种表示方法,你得到勾股定理了吗?
(a+b)
c
2
+
1
2
ab×4
验证勾股定理:
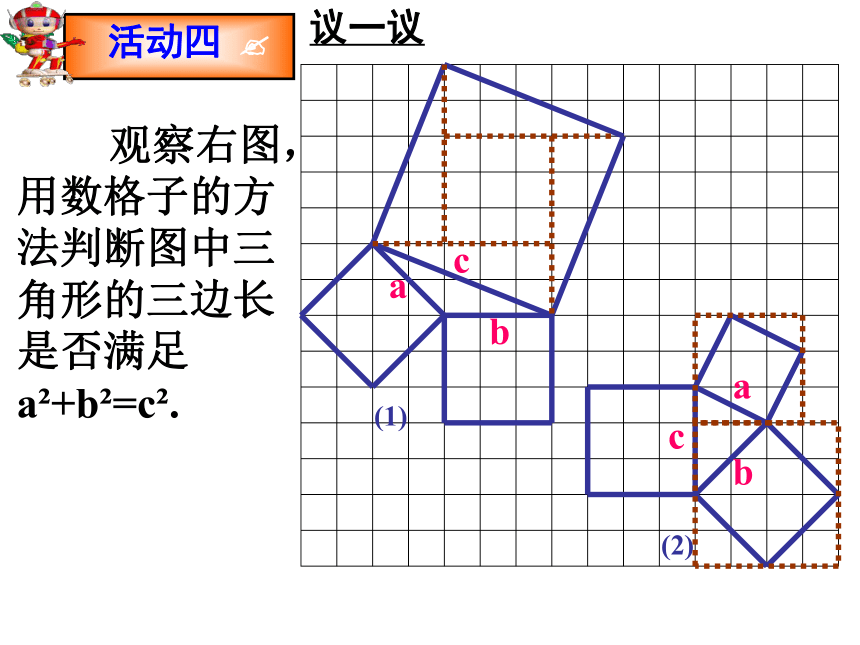
议一议
a
b
c
(1)
b
a
c
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
活动四
课堂练习: 一判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为_____,斜边为上的高为______.
24
4.8
学以致用
c
a
b
1、已知:a=3,
b=4,求c
2、已知: c =10,a=6,求b
3、已知: c =13,a=5,
求阴影总分面积
a
c
小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?
动脑筋
58厘米
46厘米
74厘米
活动五
∴售货员没搞错
∵
荧屏对角线大约为74厘米
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?
A
学以致用
4000米
5000米
20秒后
B
C
练一练
1、已知:∠C=90°,a:b=3:4,c=10,求a和b
2、已知:△ABC,AB=AC=17,
BC=16,则高AD=___,
S△ABC=___
c
a
b
1、利用数格子的方法,探索了直角三角形的三边关系,得到勾股定理:
即直角三角形两直角边的平方和等于斜边的平方
C
c
b
a
A
B
A的面积+B的面积=C的面积
a2+b2=c2
回顾 &小结:
1. 如图,你能解决这个问题吗?
3
5
x
┓
练一练
2. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
C
D
D
A
B
C
3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
唐僧:此番取经应当找个快捷方式! 悟空:坐飞机比骑马快! 八戒:神六更快! 沙僧拿出一支枪:听说这玩艺儿立马就送人上西天。
探索勾股定理
1
十二中 陈伟利
B
C
图1--1
A
(图中每个小方格代表一个单位面积)
(1)观察图
正方形A中含有 个小方格,即A的面积是_____位面积;
正方形B中含有 个小方格,即B的面积是_____个单位面积;
正方形C中含有 个小方格,即C的面积是____个单位面积。
9
9
18
9
9
18
观察 & 发现
活动一
图1—2
A
B
C
(2)观察图2:
正方形A、B、C中各有多少个小方格?它们的面积各是多少?
A的面积+ B的面积= C的面积
(3)你能发现图1与2中的三个正方形的面积有什么关系吗?
(1)观察图并填写下表:
A的面积 B的面积 C的面积
图1-3
图1-4
(2)三个正方形A,B,C的面积之间有什么关系?
16
9
25
4
9
13
A
B
C
图1--4
A
B
C
图1--3
A的面积+B的面积=C的面积
活动二
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
b
a
c
a2+b2=c2
活动三
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理
c
a
b
勾
股
弦
有人利用这4个直角三角形拼出了右图,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为 ——————————
又可以表示为:———————
a
a
a
a
b
b
b
b
c
c
c
c
对比两种表示方法,你得到勾股定理了吗?
(a+b)
c
2
+
1
2
ab×4
验证勾股定理:
议一议
a
b
c
(1)
b
a
c
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
活动四
课堂练习: 一判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为_____,斜边为上的高为______.
24
4.8
学以致用
c
a
b
1、已知:a=3,
b=4,求c
2、已知: c =10,a=6,求b
3、已知: c =13,a=5,
求阴影总分面积
a
c
小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?
动脑筋
58厘米
46厘米
74厘米
活动五
∴售货员没搞错
∵
荧屏对角线大约为74厘米
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?
A
学以致用
4000米
5000米
20秒后
B
C
练一练
1、已知:∠C=90°,a:b=3:4,c=10,求a和b
2、已知:△ABC,AB=AC=17,
BC=16,则高AD=___,
S△ABC=___
c
a
b
1、利用数格子的方法,探索了直角三角形的三边关系,得到勾股定理:
即直角三角形两直角边的平方和等于斜边的平方
C
c
b
a
A
B
A的面积+B的面积=C的面积
a2+b2=c2
回顾 &小结:
1. 如图,你能解决这个问题吗?
3
5
x
┓
练一练
2. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
C
D
D
A
B
C
3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
唐僧:此番取经应当找个快捷方式! 悟空:坐飞机比骑马快! 八戒:神六更快! 沙僧拿出一支枪:听说这玩艺儿立马就送人上西天。
