人教版 数学九年级上册课件:23.2.1 中心对称(共24张PPT)
文档属性
| 名称 | 人教版 数学九年级上册课件:23.2.1 中心对称(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 14:36:41 | ||
图片预览





文档简介
(共24张PPT)
23.2.1
中心对称
23.2
中心对称
3.掌握中心对称的性质及其应用.
1.理解中心对称的定义.
2.探究中心对称的性质.
学习目标
O
创设情境
导入新课
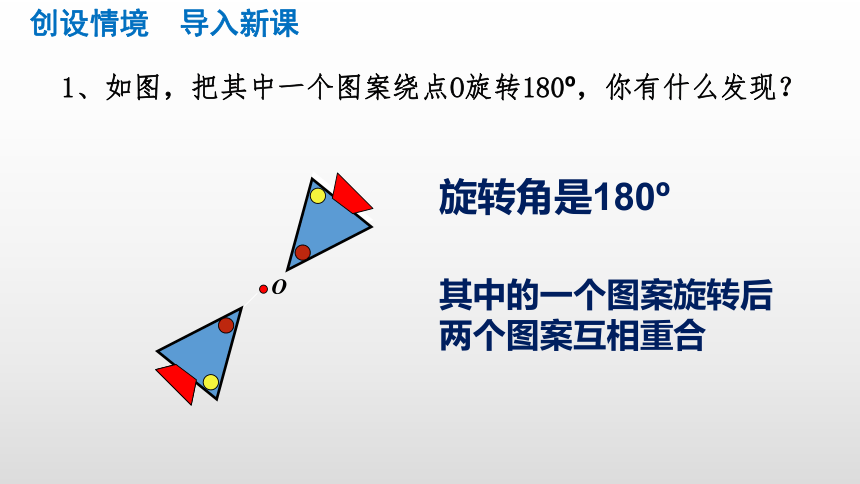
1、如图,把其中一个图案绕点O旋转180?,你有什么发现?
旋转角是180?
其中的一个图案旋转后两个图案互相重合
A
O
D
B
C
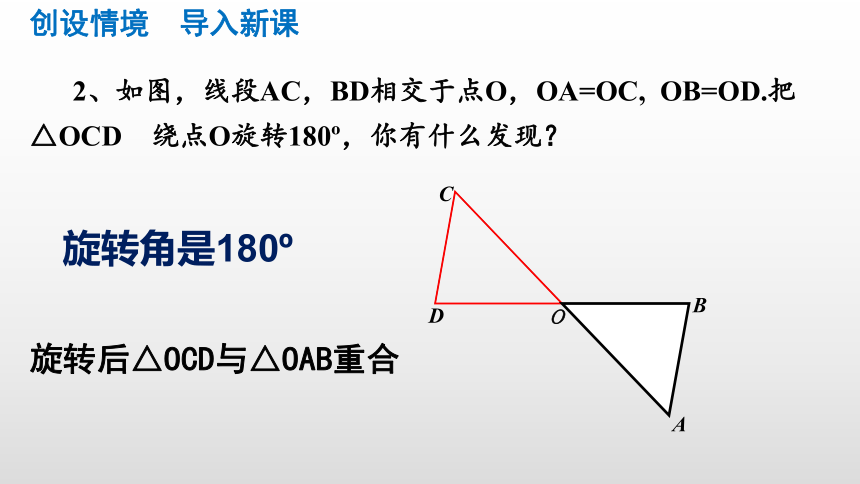
2、如图,线段AC,BD相交于点O,OA=OC,
OB=OD.把△OCD
绕点O旋转180?,你有什么发现?
创设情境
导入新课
旋转角是180?
旋转后△OCD与△OAB重合
把一个图形
,如果它
,那么就说这两个图形关于这个点
或
,这个点叫做
.
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
合作探究
感受新知
中心对称的概念
A
O
D
B
C
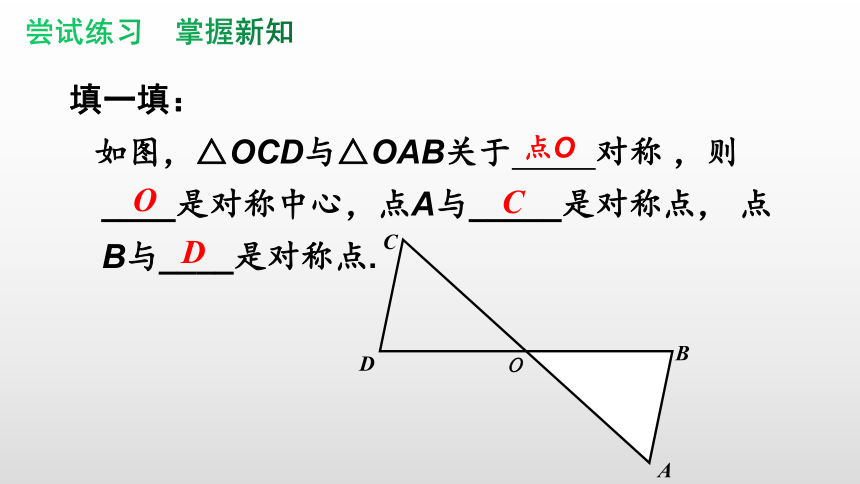
填一填:
如图,△OCD与△OAB关于
对称
,则____是对称中心,点A与_____是对称点,
点B与____是对称点.
O
B
C
A
D
O
C
D
尝试练习
掌握新知
点O
【思考】两个图形成中心对称需要具备什么条件?
两个图形成中心对称须具备三个条件:
①能找到一个对称中心;
②旋转角为180°;
③这两个图形旋转后能重合.
合作探究
感受新知
1.中心对称是一种特殊的旋转,其旋转角是180
°.
2.中心对称是两个图形之间一种特殊的位置关系.
【归纳】
合作探究
感受新知
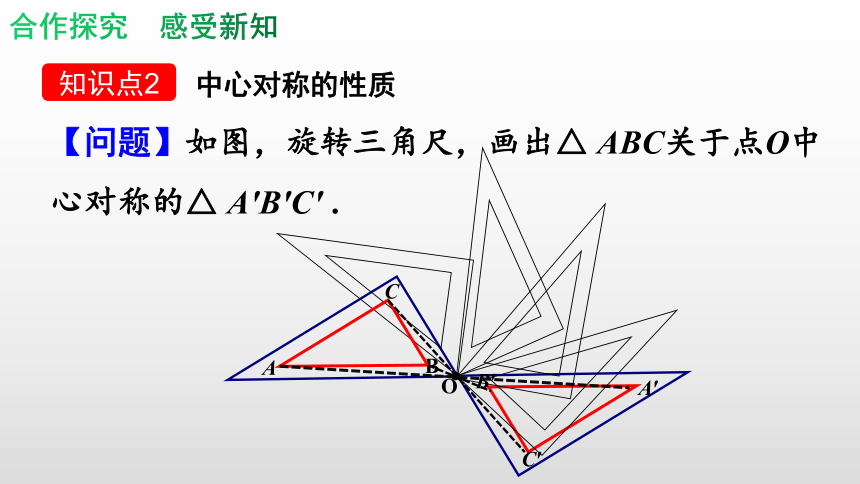
【问题】如图,旋转三角尺,画出△
ABC关于点O中心对称的△
A′B′C′
.
A′
C
A
B
B′
C′
O
●
中心对称的性质
知识点2
合作探究
感受新知
1.中心对称的两个图形中,对称点所连线段都经过对称中心,且被对称中心所平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等图形.
中心对称的性质
归纳
例1
(1)如图,选择点O为对称中心,画出点A关于点O的对称点A'
O
合作探究
感受新知
A
如图,连接AO,在AO的延长线上截取OA'=OA,即可以求得点A关于点O的对称点A'
A'
(2)如图,选择点0为对称中心,画出与△ABC关于点O对称的△A'B'C'
B'
A'
O
C
B
A
C'
②依次连接A'B',B'C',C'A',就可得到与△ABC关于点O对称的△A'B'C'
如图,①作出A、B、C三点关于点O的对称点A'B'C'
尝试练习
掌握新知
1、分别画出下列图形关于点O对称的图形
0
0
尝试练习
掌握新知
2.图中的两个四边形关于某点对称,找出它们的对称中心。
O
则点O就是所求的对称中心
3.如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是(
)
A.AD∥EF,AB∥GF
B.BO=GO
C.CD=HE,BC=GH
D.DO=HO
D
G
尝试练习
掌握新知
4.如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高为________.
解析:设AB边上的高为h,因为△AOB的面积
是12,AB=3,易得h=8.
又因为△AOB与△DOC成中心对称,△COD≌△AOB,
所以△DOC中CD边上的高是8.
8
尝试练习
掌握新知
(2016?中考)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1,C1的坐标.
连接中考
尝试练习
掌握新知
解:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,∵D1、D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A、D的坐标分别是(0,4)、(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B、C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1、C1的坐标分别是(2,1)、(2,3),
综上,可得:顶点B、C、B1、C1的坐标分别是(﹣2,4),(﹣2,2)、(2,1)、(2,3).
巩固练习
1.判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.(
)
(2)成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形.
(
)
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形.
(
)
√
√
×
基础巩固题
尝试练习
掌握新知
2.
如下所示的4组图形中,左边数字与右边数字成中心对称的有(
)
A.1组
B.2组
C.3组
D.4组
D
3.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( )
A.2
B.4
C.6
D.8
A
B
C
D
O
B
尝试练习
掌握新知
如图,已知等边三角形ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
A′
B′
C′
O
A
B
C
能力提升题
1.连接AO并且延长AO至A′,使AO=A′O;
2.连接BO并且延长BO至B′,使BO=B′O;
3.连接CO并且延长CO至C′,使CO=C′O;
则△A′B′C′即为所求.
作法:
尝试练习
掌握新知
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,
求四边形ABFE的面积.
拓广探索题
尝试练习
掌握新知
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形
(2)S四边形ABFE=4S△ABC=12
cm2.
课堂检测
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
能找到一个对称中心
两个图形旋转后重合
课堂小结
23.2.1
中心对称
23.2
中心对称
3.掌握中心对称的性质及其应用.
1.理解中心对称的定义.
2.探究中心对称的性质.
学习目标
O
创设情境
导入新课
1、如图,把其中一个图案绕点O旋转180?,你有什么发现?
旋转角是180?
其中的一个图案旋转后两个图案互相重合
A
O
D
B
C
2、如图,线段AC,BD相交于点O,OA=OC,
OB=OD.把△OCD
绕点O旋转180?,你有什么发现?
创设情境
导入新课
旋转角是180?
旋转后△OCD与△OAB重合
把一个图形
,如果它
,那么就说这两个图形关于这个点
或
,这个点叫做
.
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
合作探究
感受新知
中心对称的概念
A
O
D
B
C
填一填:
如图,△OCD与△OAB关于
对称
,则____是对称中心,点A与_____是对称点,
点B与____是对称点.
O
B
C
A
D
O
C
D
尝试练习
掌握新知
点O
【思考】两个图形成中心对称需要具备什么条件?
两个图形成中心对称须具备三个条件:
①能找到一个对称中心;
②旋转角为180°;
③这两个图形旋转后能重合.
合作探究
感受新知
1.中心对称是一种特殊的旋转,其旋转角是180
°.
2.中心对称是两个图形之间一种特殊的位置关系.
【归纳】
合作探究
感受新知
【问题】如图,旋转三角尺,画出△
ABC关于点O中心对称的△
A′B′C′
.
A′
C
A
B
B′
C′
O
●
中心对称的性质
知识点2
合作探究
感受新知
1.中心对称的两个图形中,对称点所连线段都经过对称中心,且被对称中心所平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等图形.
中心对称的性质
归纳
例1
(1)如图,选择点O为对称中心,画出点A关于点O的对称点A'
O
合作探究
感受新知
A
如图,连接AO,在AO的延长线上截取OA'=OA,即可以求得点A关于点O的对称点A'
A'
(2)如图,选择点0为对称中心,画出与△ABC关于点O对称的△A'B'C'
B'
A'
O
C
B
A
C'
②依次连接A'B',B'C',C'A',就可得到与△ABC关于点O对称的△A'B'C'
如图,①作出A、B、C三点关于点O的对称点A'B'C'
尝试练习
掌握新知
1、分别画出下列图形关于点O对称的图形
0
0
尝试练习
掌握新知
2.图中的两个四边形关于某点对称,找出它们的对称中心。
O
则点O就是所求的对称中心
3.如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是(
)
A.AD∥EF,AB∥GF
B.BO=GO
C.CD=HE,BC=GH
D.DO=HO
D
G
尝试练习
掌握新知
4.如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高为________.
解析:设AB边上的高为h,因为△AOB的面积
是12,AB=3,易得h=8.
又因为△AOB与△DOC成中心对称,△COD≌△AOB,
所以△DOC中CD边上的高是8.
8
尝试练习
掌握新知
(2016?中考)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1,C1的坐标.
连接中考
尝试练习
掌握新知
解:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,∵D1、D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A、D的坐标分别是(0,4)、(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B、C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1、C1的坐标分别是(2,1)、(2,3),
综上,可得:顶点B、C、B1、C1的坐标分别是(﹣2,4),(﹣2,2)、(2,1)、(2,3).
巩固练习
1.判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.(
)
(2)成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形.
(
)
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形.
(
)
√
√
×
基础巩固题
尝试练习
掌握新知
2.
如下所示的4组图形中,左边数字与右边数字成中心对称的有(
)
A.1组
B.2组
C.3组
D.4组
D
3.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( )
A.2
B.4
C.6
D.8
A
B
C
D
O
B
尝试练习
掌握新知
如图,已知等边三角形ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
A′
B′
C′
O
A
B
C
能力提升题
1.连接AO并且延长AO至A′,使AO=A′O;
2.连接BO并且延长BO至B′,使BO=B′O;
3.连接CO并且延长CO至C′,使CO=C′O;
则△A′B′C′即为所求.
作法:
尝试练习
掌握新知
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,
求四边形ABFE的面积.
拓广探索题
尝试练习
掌握新知
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形
(2)S四边形ABFE=4S△ABC=12
cm2.
课堂检测
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
能找到一个对称中心
两个图形旋转后重合
课堂小结
同课章节目录
