《2.1、探索勾股定理》
图片预览



文档简介
(共20张PPT)
探索勾股定理
济宁十二中: 陈伟利
没有人能让我输,除非我自己不想赢!
我们知道,任意三角形的三条边必须满足定理:三角形的两边之和大于第三边。对于等腰三角形和等边三角形的边,除满足三边关系定理外,它们还分别存在着两边相等和三边相等的特殊关系。那么对于直角三角形的边,除满足三边关系定理外,它们之间也存在着特殊的关系,这就是我们这一节要研究的问题:勾股定理。
创设问题情境,激发学习热情
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
你是怎样得到上面的结果的?与同伴交流交流。
1
2
3
(2)(3)
C
A
B
A
B
C
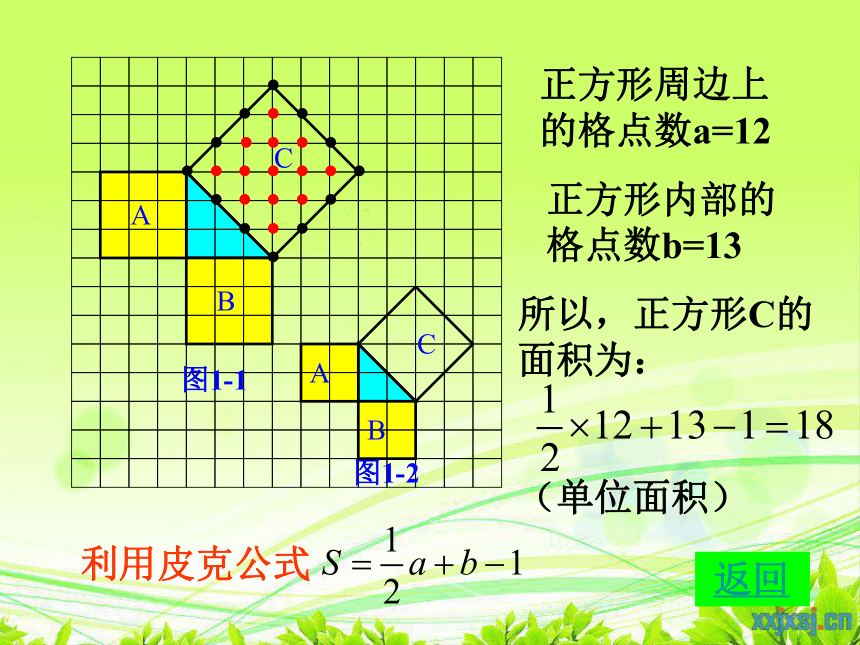
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
(单位面积)
返回
图1-1
图1-2
A
B
C
A
B
C
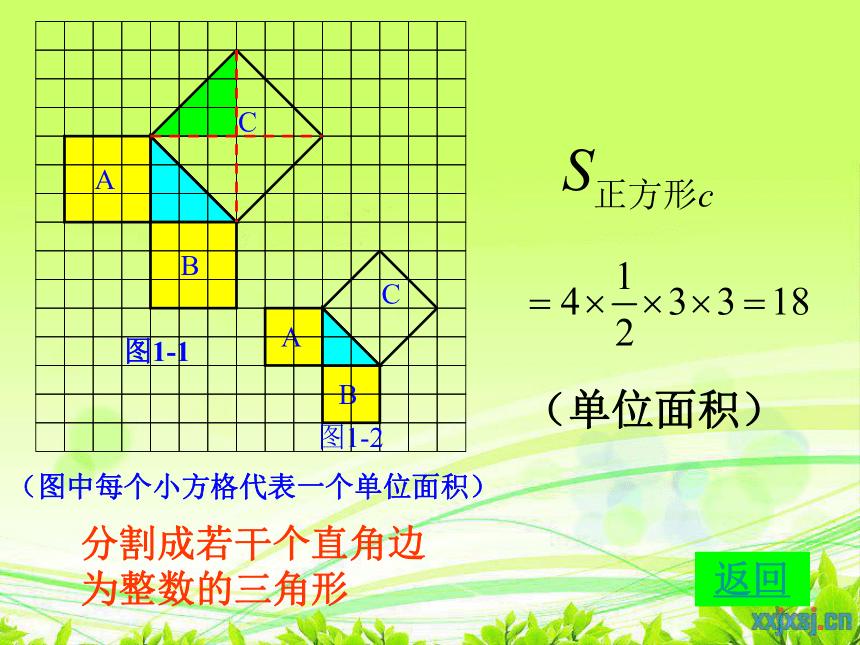
(图中每个小方格代表一个单位面积)
图1-1
图1-2
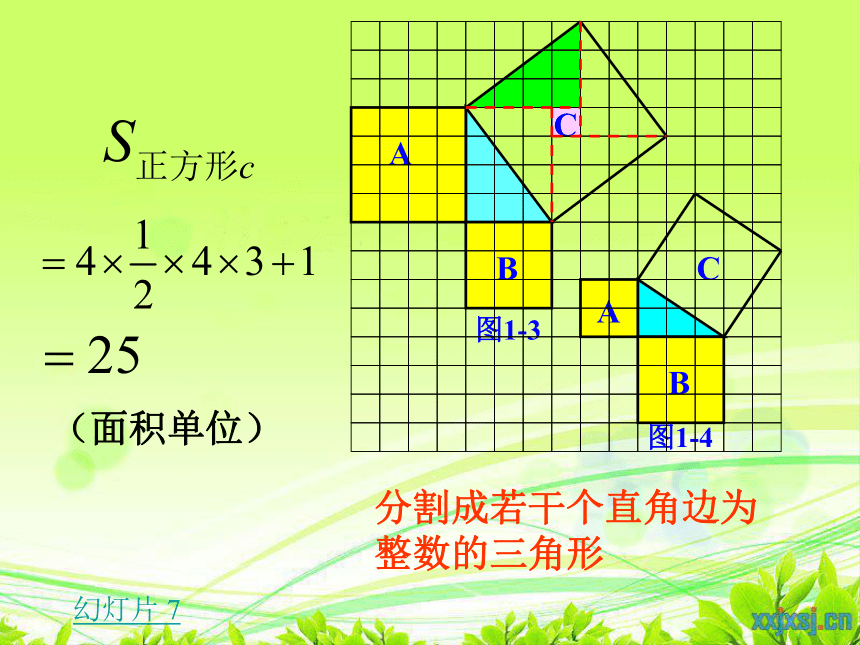
分割成若干个直角边为整数的三角形
(单位面积)
返回
A
B
C
A
B
C
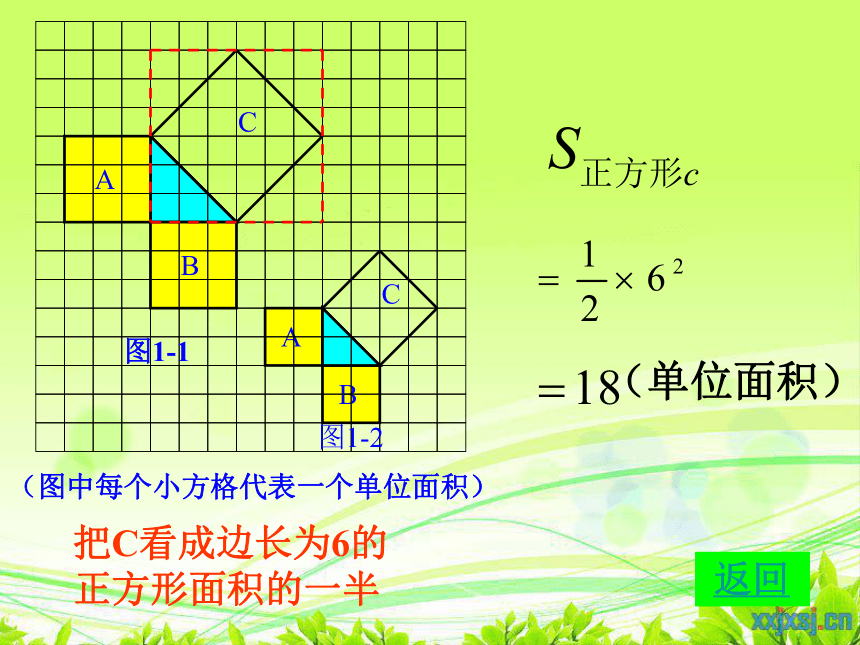
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
把C看成边长为6的正方形面积的一半
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
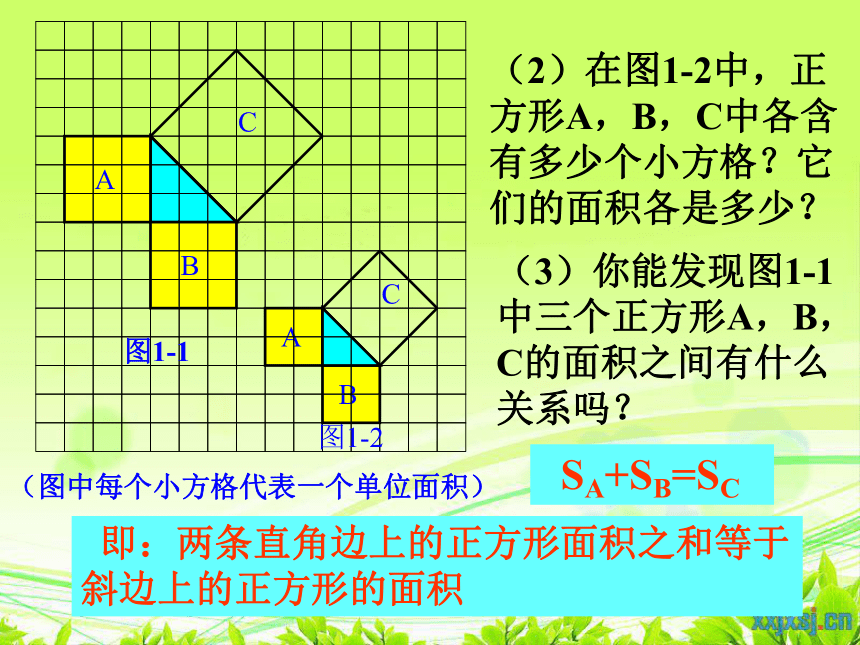
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
A
B
C
图1-3
A
B
C
图1-4
(1)观察图1-3、图1-4,并填写右表:
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流。
做一做
幻灯片 9
A
B
C
图1-3
A
B
C
图1-4
分割成若干个直角边为整数的三角形
(面积单位)
幻灯片 7
A
B
C
图1-3
A
B
C
图1-4
(2)三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
幻灯片 7
A
B
C
图1-3
A
B
C
图1-4
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?
议一议
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
我国古代称直角三角形的较短的直角边为勾,较长的直角边为股,斜边为弦,这就是勾股定理的由来。
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
想一想
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
想一想
∴售货员没搞错
∵
荧屏对角线大约为74厘米
1、已知在Rt△ABC中,∠C=90°。
①若a=3,b=4,则c=________;
②若a=40,b=9,则c=________;
③若a=6,c=10,则b=_______;
④若c=25,b=15,则a=________。
2、已知在Rt△ABC中,∠C=90°,AB=10。
①若∠A=30°,则BC=______,AC=_______;
②若∠A=45°,则BC=______,AC=_______。
3、已知等边三角形ABC的边长是6cm。求:
(1)高AD的长;
(2)△ABC的面积。
探索勾股定理
济宁十二中: 陈伟利
没有人能让我输,除非我自己不想赢!
我们知道,任意三角形的三条边必须满足定理:三角形的两边之和大于第三边。对于等腰三角形和等边三角形的边,除满足三边关系定理外,它们还分别存在着两边相等和三边相等的特殊关系。那么对于直角三角形的边,除满足三边关系定理外,它们之间也存在着特殊的关系,这就是我们这一节要研究的问题:勾股定理。
创设问题情境,激发学习热情
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
你是怎样得到上面的结果的?与同伴交流交流。
1
2
3
(2)(3)
C
A
B
A
B
C
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
(单位面积)
返回
图1-1
图1-2
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
分割成若干个直角边为整数的三角形
(单位面积)
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
把C看成边长为6的正方形面积的一半
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
A
B
C
图1-3
A
B
C
图1-4
(1)观察图1-3、图1-4,并填写右表:
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流。
做一做
幻灯片 9
A
B
C
图1-3
A
B
C
图1-4
分割成若干个直角边为整数的三角形
(面积单位)
幻灯片 7
A
B
C
图1-3
A
B
C
图1-4
(2)三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
幻灯片 7
A
B
C
图1-3
A
B
C
图1-4
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?
议一议
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
我国古代称直角三角形的较短的直角边为勾,较长的直角边为股,斜边为弦,这就是勾股定理的由来。
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
想一想
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
想一想
∴售货员没搞错
∵
荧屏对角线大约为74厘米
1、已知在Rt△ABC中,∠C=90°。
①若a=3,b=4,则c=________;
②若a=40,b=9,则c=________;
③若a=6,c=10,则b=_______;
④若c=25,b=15,则a=________。
2、已知在Rt△ABC中,∠C=90°,AB=10。
①若∠A=30°,则BC=______,AC=_______;
②若∠A=45°,则BC=______,AC=_______。
3、已知等边三角形ABC的边长是6cm。求:
(1)高AD的长;
(2)△ABC的面积。
