《2.2、勾股数——能得到直角三角形吗》
文档属性
| 名称 | 《2.2、勾股数——能得到直角三角形吗》 |

|
|
| 格式 | rar | ||
| 文件大小 | 629.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-24 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
2.2勾股数
——能得到直角三角形吗
七年级数学(上册) 鲁教版
济宁十二中学 陈伟利
A
B
C
D
E
F
49
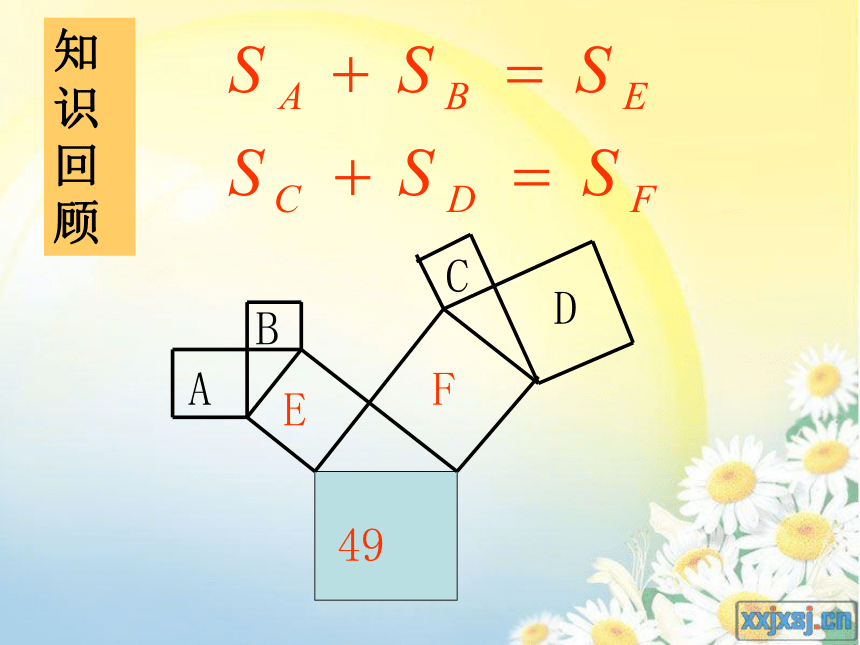
知识回顾
同学们你们知道古埃及人用什么方法得到直角
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,一个工匠同时握住
绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,
拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
2
1、这段课文说得是什么?
2、依照课文所说的做一做:把一条线段分成12等份,在第三、第七等分处折成一个三角形,并量一量最大角是多少度。
3、这个三角形的三边分别是3、4、5等分,这三个数有什么样的数量关系?
32+42=52
做一做:
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 6, 8, 10; 8,15,17.
(1)这三组数都满足a2 +b2=c2吗?
(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数
勾股定理的逆定理
在 ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则 ABC为直角三角形;
若a2 +b2>c2, 则 ABC为锐角三角形;
若a2 +b213
A
B
C
D
A
B
C
D
3
4
5
12
例1 一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示,这个 零件符合要求吗?
练习:P31的随堂练习
1. 如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是 ( )
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
B
A
三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是: ( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.
已知 ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, _____是最大角.
5. 以 ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
A
直角
直角
∠BAC
A
D
C
B
四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个四边形的面积.
7、请你写出三组勾股数;
8、一组勾股数的倍数一定是勾股数吗?为什么
小结:
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2,
那么这个三角形是直角三角形
勾股数:
满足a2 +b2=c2的三个正整数,称为勾股数
补充思考题: △ABC中,AB=17cm, BC=30cm, BC上中线AD=8cm,请你判断△ABC的形状,并说明理由。
再见
2.2勾股数
——能得到直角三角形吗
七年级数学(上册) 鲁教版
济宁十二中学 陈伟利
A
B
C
D
E
F
49
知识回顾
同学们你们知道古埃及人用什么方法得到直角
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,一个工匠同时握住
绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,
拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
2
1、这段课文说得是什么?
2、依照课文所说的做一做:把一条线段分成12等份,在第三、第七等分处折成一个三角形,并量一量最大角是多少度。
3、这个三角形的三边分别是3、4、5等分,这三个数有什么样的数量关系?
32+42=52
做一做:
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 6, 8, 10; 8,15,17.
(1)这三组数都满足a2 +b2=c2吗?
(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数
勾股定理的逆定理
在 ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则 ABC为直角三角形;
若a2 +b2>c2, 则 ABC为锐角三角形;
若a2 +b2
A
B
C
D
A
B
C
D
3
4
5
12
例1 一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示,这个 零件符合要求吗?
练习:P31的随堂练习
1. 如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是 ( )
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
B
A
三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是: ( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.
已知 ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, _____是最大角.
5. 以 ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
A
直角
直角
∠BAC
A
D
C
B
四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个四边形的面积.
7、请你写出三组勾股数;
8、一组勾股数的倍数一定是勾股数吗?为什么
小结:
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2,
那么这个三角形是直角三角形
勾股数:
满足a2 +b2=c2的三个正整数,称为勾股数
补充思考题: △ABC中,AB=17cm, BC=30cm, BC上中线AD=8cm,请你判断△ABC的形状,并说明理由。
再见
