《第二章、勾股定理复习》课件
图片预览





文档简介
(共15张PPT)
《勾股定理》复习
十二中: 陈伟利
A
B
C
如果直角三角形两直角边分别为a,b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a2 + b2 = c2
勾股定理
A的面积+B的面积=C的面积
a
b
c
一、知识网络
直角三角形:
角:
1、三内角之和为180。
2、两内角互余
边:
1、任意两边之和大于第三边
2、任意两边之差小于第三边
3、勾股定理-----应用
直角三角形的判定及应用
二、复习练:
1、判断由如下三组线段a、b、c组成的三角形是不是直角三角形
(1)a=10 b=24 c=26
(2)a=1.5 b=2 c=2.5
(3)a=b=2 c=4
2、在直角三角形ABC中,∠C=90.
(1)已知 a=b=5,求c
(2)已知 a=1 c=2 求b
(3)已知 a:b=1:2 且c=5,求a、b
(4)已知∠A=1/2 ∠B,且a=2,求b、c
三、典例解析
例1、已知直角三角形的两直角边之比为3:4, 斜边为10。 求直角三角形的两直角边
解:设两直角边为3x 、4x,由题意知:
(3x)2 + (4x )2=100
25x 2=100
X =2
3X=6,4X=8
所以 两直角边长分别为6,8
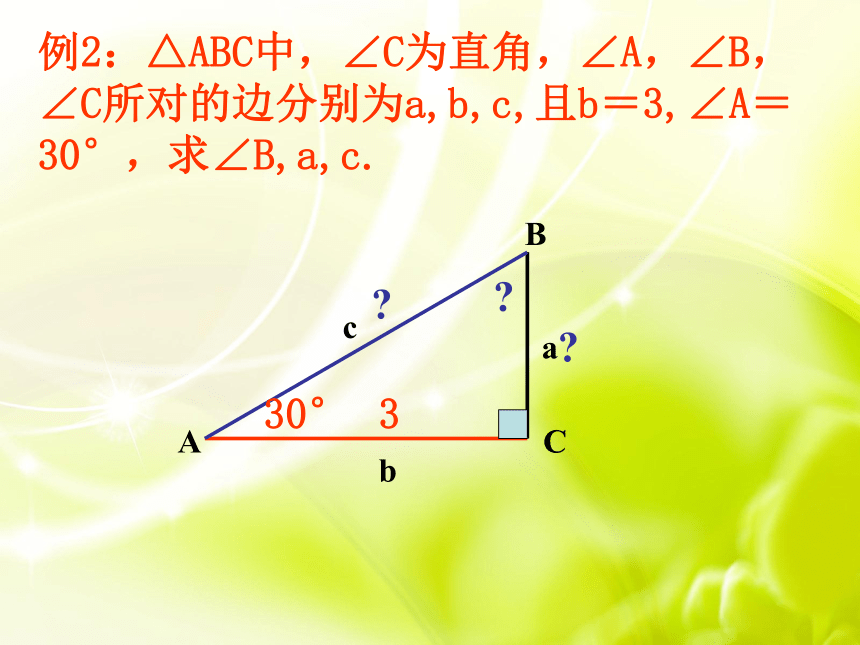
例2:△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.
A
B
C
a
b
c
3
30°
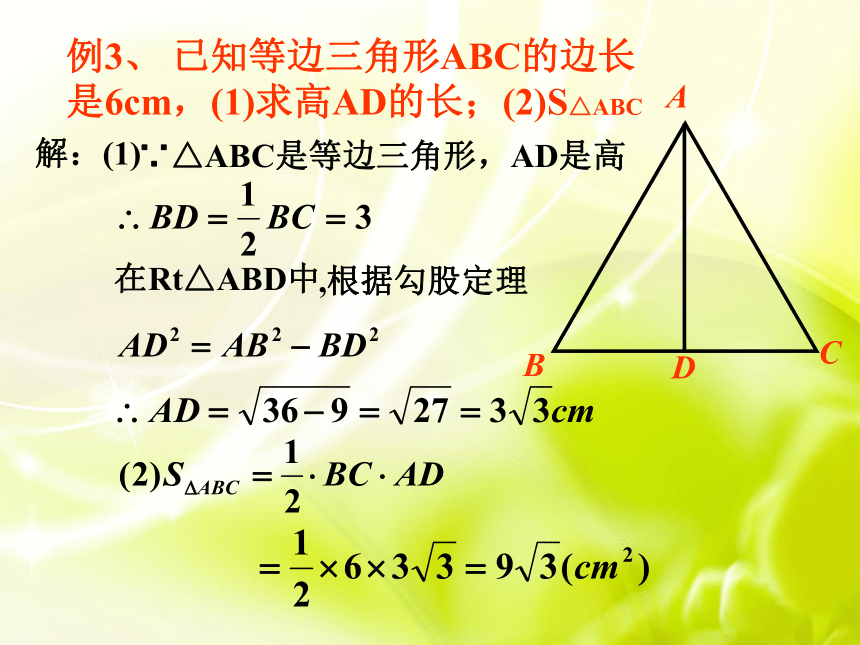
例3、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
,根据勾股定理
例4 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求CA的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
1,在直角三角形ABC中,∠C=90。,BC=12,
AB一AC=8,则AC=----------
2,在三角形ABC中,三边a b c , 若有c2=5a2 ,
b2 =4a2, 则三角形ABC是----------三角形。
3,在三角形ABC中,若三边长分别为9,12,15,则以两个这样的三角形所拼成的矩形面积为---------
4,把直角三角形两直角边同时扩大到原来的2倍,则其 斜边扩大到原来的( )
A、2倍 B、4倍 C、3倍 D、5倍
四、达标检测:
5
直角
108
A
例5: 如图,公路MN和公路PQ在点P处交汇。点A处有一所中学,AP=160m,点A到公路MN的距离为80m。假设拖拉机行驶时,周围100m以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受影响,已知拖拉机的速度18km/h,那么学校受影响的时间为多少秒?
M
N
P
Q
A
解:因为A到MN 的距离为80m,而拖拉机的噪音范围100m以内,80<100,所以拖拉机会影响学校
B
D
C
5、在三角形ABC中,∠C=90。 周长为60,斜边与一条直角边的比为13:5,则这个三角形的三边长分别为( )
A、5,4,3 B、13,12,5
C、10,8,6 D、26,24,10
6、以面积为9的正方形的对角线为边,作一个正方形,其面 积为( ) A、9、 B、13 C、18 D、24
7、如果三角形ABC的三边长分别为m 2-1,2m ,m2+1,(m>1) 那么( )
A、三角形ABC是直角三角形,且斜边长为m2+1
B、三角形ABC是直角三角形,且斜边长是2m
C 、三角形ABC是直角三角形,但斜边长需由m 的大小而定
D、三角形ABC不是直角三角形
D
C
A
8、如图是一个三级台阶,它的每一级的长、宽、高分别等于55寸,10寸和6寸。A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,请想一想,这只蚂蚁从A点出发沿着台阶爬到B点最短路线是多少?
A
B
A
B
亲爱的同学,通过今天的复习,对“勾股定理”的知识还有疑惑吗?
再 见!
《勾股定理》复习
十二中: 陈伟利
A
B
C
如果直角三角形两直角边分别为a,b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a2 + b2 = c2
勾股定理
A的面积+B的面积=C的面积
a
b
c
一、知识网络
直角三角形:
角:
1、三内角之和为180。
2、两内角互余
边:
1、任意两边之和大于第三边
2、任意两边之差小于第三边
3、勾股定理-----应用
直角三角形的判定及应用
二、复习练:
1、判断由如下三组线段a、b、c组成的三角形是不是直角三角形
(1)a=10 b=24 c=26
(2)a=1.5 b=2 c=2.5
(3)a=b=2 c=4
2、在直角三角形ABC中,∠C=90.
(1)已知 a=b=5,求c
(2)已知 a=1 c=2 求b
(3)已知 a:b=1:2 且c=5,求a、b
(4)已知∠A=1/2 ∠B,且a=2,求b、c
三、典例解析
例1、已知直角三角形的两直角边之比为3:4, 斜边为10。 求直角三角形的两直角边
解:设两直角边为3x 、4x,由题意知:
(3x)2 + (4x )2=100
25x 2=100
X =2
3X=6,4X=8
所以 两直角边长分别为6,8
例2:△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.
A
B
C
a
b
c
3
30°
例3、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
,根据勾股定理
例4 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求CA的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
1,在直角三角形ABC中,∠C=90。,BC=12,
AB一AC=8,则AC=----------
2,在三角形ABC中,三边a b c , 若有c2=5a2 ,
b2 =4a2, 则三角形ABC是----------三角形。
3,在三角形ABC中,若三边长分别为9,12,15,则以两个这样的三角形所拼成的矩形面积为---------
4,把直角三角形两直角边同时扩大到原来的2倍,则其 斜边扩大到原来的( )
A、2倍 B、4倍 C、3倍 D、5倍
四、达标检测:
5
直角
108
A
例5: 如图,公路MN和公路PQ在点P处交汇。点A处有一所中学,AP=160m,点A到公路MN的距离为80m。假设拖拉机行驶时,周围100m以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受影响,已知拖拉机的速度18km/h,那么学校受影响的时间为多少秒?
M
N
P
Q
A
解:因为A到MN 的距离为80m,而拖拉机的噪音范围100m以内,80<100,所以拖拉机会影响学校
B
D
C
5、在三角形ABC中,∠C=90。 周长为60,斜边与一条直角边的比为13:5,则这个三角形的三边长分别为( )
A、5,4,3 B、13,12,5
C、10,8,6 D、26,24,10
6、以面积为9的正方形的对角线为边,作一个正方形,其面 积为( ) A、9、 B、13 C、18 D、24
7、如果三角形ABC的三边长分别为m 2-1,2m ,m2+1,(m>1) 那么( )
A、三角形ABC是直角三角形,且斜边长为m2+1
B、三角形ABC是直角三角形,且斜边长是2m
C 、三角形ABC是直角三角形,但斜边长需由m 的大小而定
D、三角形ABC不是直角三角形
D
C
A
8、如图是一个三级台阶,它的每一级的长、宽、高分别等于55寸,10寸和6寸。A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,请想一想,这只蚂蚁从A点出发沿着台阶爬到B点最短路线是多少?
A
B
A
B
亲爱的同学,通过今天的复习,对“勾股定理”的知识还有疑惑吗?
再 见!
