《勾股定理》复习课件
图片预览







文档简介
(共48张PPT)
《勾股定理》复习
课件改编: 陈伟利
A
B
C
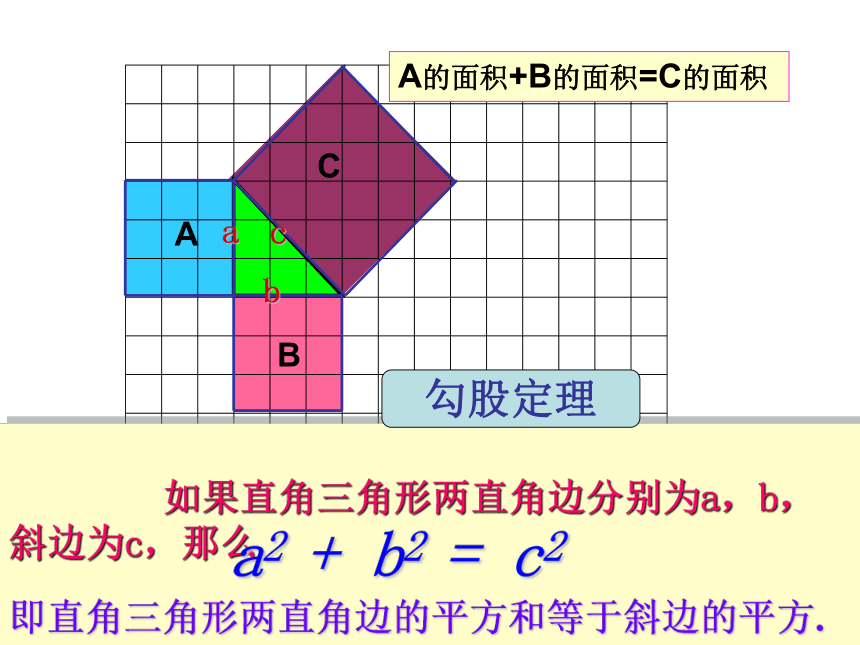
如果直角三角形两直角边分别为a,b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a2 + b2 = c2
勾股定理
A的面积+B的面积=C的面积
a
b
c
1.如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
2.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形。
勾股定理专题
一.勾股定理与面积
四.分类思想
二.方程思想
三.展开思想
一.勾股定理与面积
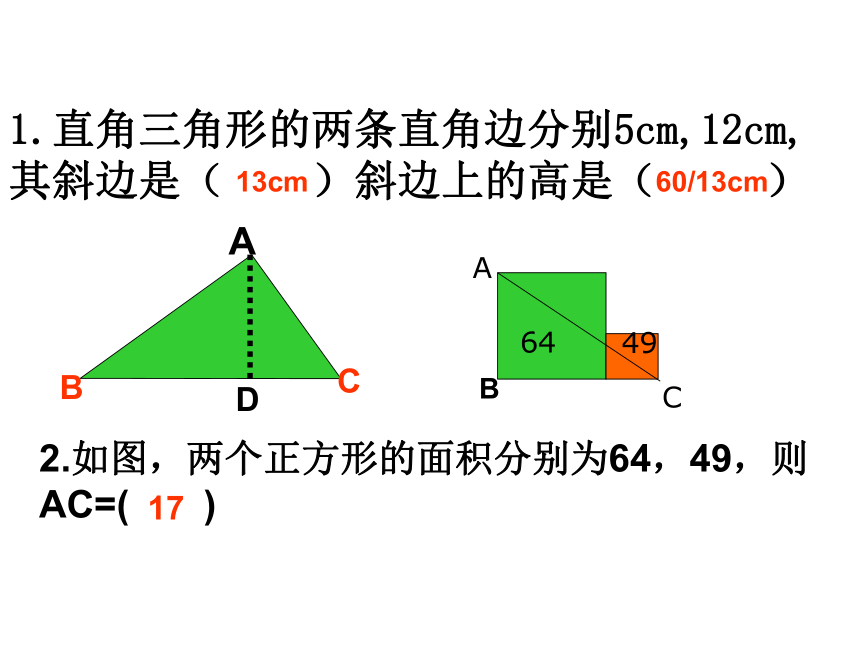
1.直角三角形的两条直角边分别5cm,12cm,其斜边是( )斜边上的高是( )
2.如图,两个正方形的面积分别为64,49,则AC=( )
A
C
64
49
B
A
B
C
13cm
60/13cm
17
D
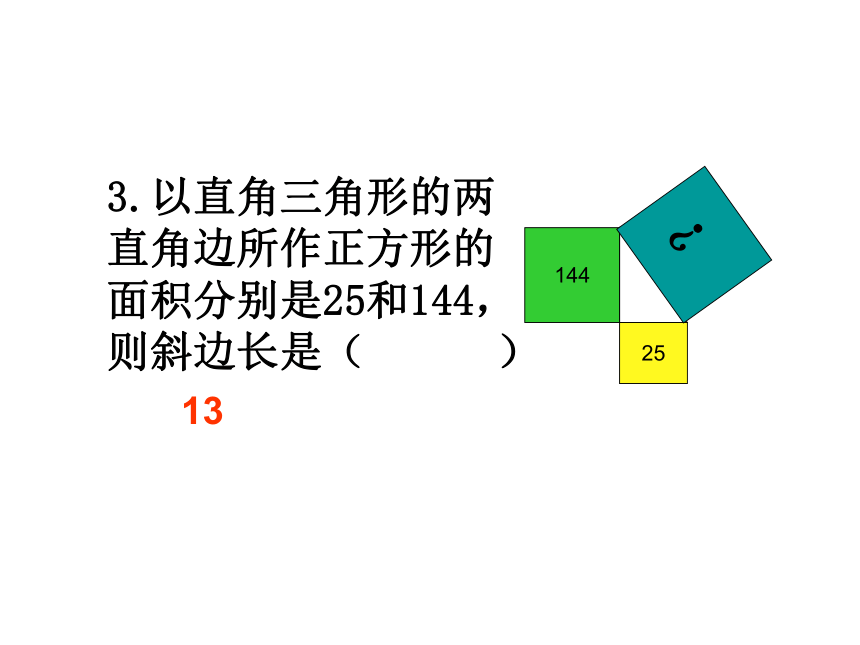
3.以直角三角形的两直角边所作正方形的面积分别是25和144,则斜边长是( )
13
25
144
?
4.如图,分别以直角三角形三边为半径作半圆,则这三个半圆A,B,C的面积之间的关系( )
SA+SB=SC
D
A
B
C
a
b
c
5.若以直角三角形三边为边向外作正三角形呢?
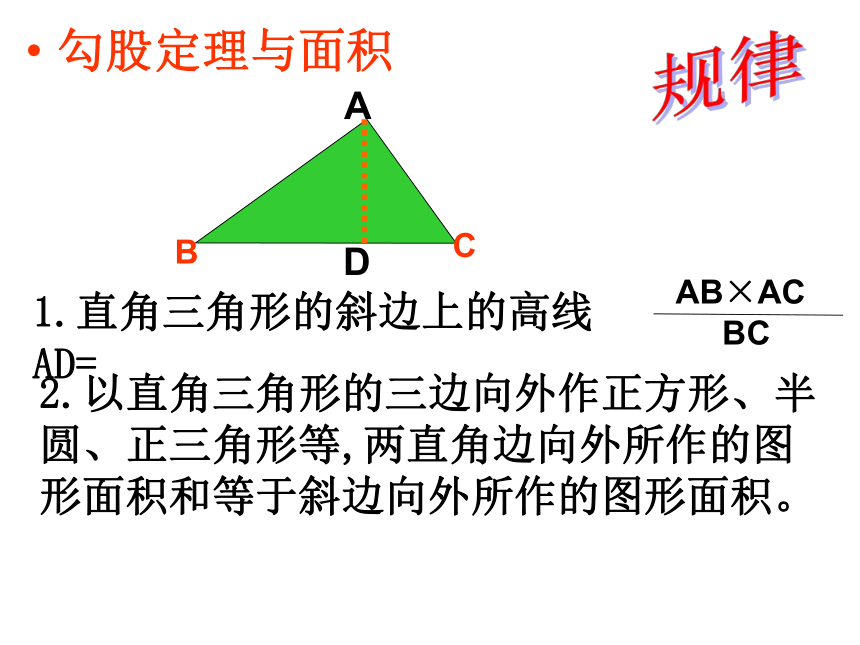
勾股定理与面积
1.直角三角形的斜边上的高线AD=
A
B
C
D
AB×AC
BC
2.以直角三角形的三边向外作正方形、半圆、正三角形等,两直角边向外所作的图形面积和等于斜边向外所作的图形面积。
二.方程思想
1.在直角三角形中,∠C为直角,已知a:b=5:12,c=6.5,求a,b.
A
B
C
2.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,求旗杆的断裂处离地面的距离。
A
B
C
三.展开思想
1.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1.CF 2.EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
B
C
D
E
F
8
10
10
X
8-X
8-X
6
4
解:由题意得AD= BC=10CM
∴BF2=AF2-AB2=102-82
在直角三角形EFC中FC2+EC2=EF2
解,得 X=3
∴BF=6 FC=4
∵AB⊥BC
设EC=X,则EF=8-X。
即42+X2=(8-X)2
∴EC=3
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
三.展开思想
四.分类思想
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求(1)BD (2)CD (3)BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=
25
或7
A
B
C
分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
一.勾股定理与面积
1.直角三角形的斜边上的高线AD=
A
B
C
D
AB×AC
BC
2.以直角三角形的三边向外作正方形、半圆、正三角形两直角边向外所作的图形面积和等于斜边向外所作的图形面积。
二.方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.并利用两点之间线段最短,及勾股定理求解。
三.展开思想
四.分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
已知三角形ABC中,AB=10,BC=21,AC=17,求BC边上的高线AD。
A
B
C
D
解:设BD=X,则DC=21-X。
∵AD⊥BC
∴AD2=AB2-BD2=102-X2
AD2=AC2-CD2=172-(21-X)2
解,得 X=6
∴102-X2=172-(21-X)2
∴AD2=102-62=64
∴AD=8
再 见!
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
分割成若干个直角边为整数的三角形
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
把C看成边长为6的正方形面积的一半
C
A
B
A
B
C
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
图1-1
图1-2
∟
a
b
c
用四个全等的三角形拼一拼、摆一摆,看看能否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?
大正方形的面积可以表示为 ——————————
又可以表示为:———————
(a+b)
c2+1/2ab 4
a2 + b2 = c2
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
大正方形的面积可以表示为 ——————————
又可以表示为:———————
∟
a
b
c
c
(b-a) +1/2ab 4
a2 + b2 = c2
3.已知一个Rt△的两边长分别为3和4,
则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
2.下列各组数中,以a,b,c为边的三角形
不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5
④若a∶b=3∶4,c=10,
则Rt△ABC的面积为________。
②若a=15,c=25,则b=___________;
1.在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
③若c=61,b=60,则a=__________;
13
20
11
24
A
D
4.以直角三角形的两直角边所作正方形的面积
分别是25和144,则斜边长是( )
5.如图,两个正方形的面积
分别为64,49,则AC=( )
A
D
C
64
C
64
49
6.三角形的三边长为(a+b)2=c2+2ab,则这个三角形是( )
A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.
13
17
C
7.果汁饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
A
C
B
5
12
13
1)郑凯想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
2)如图,厉俊杰家有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。请你算出他家这块地的面积。
A
C
B
D
C
A
D
B
3m
12m
4m
13m
3)如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
4)如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
亲爱的同学,通过今天的复习,对“勾股定理”的知识还有疑惑吗?
印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”,请用学过的数学知识回答这个问题。
2
X+0.5
X
C
B
A
已知Rt△ABC中,∠C=90°,
若a+b=14cm,c=10cm,
求Rt△ABC的面积.
《勾股定理》复习
课件改编: 陈伟利
A
B
C
如果直角三角形两直角边分别为a,b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a2 + b2 = c2
勾股定理
A的面积+B的面积=C的面积
a
b
c
1.如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
2.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形。
勾股定理专题
一.勾股定理与面积
四.分类思想
二.方程思想
三.展开思想
一.勾股定理与面积
1.直角三角形的两条直角边分别5cm,12cm,其斜边是( )斜边上的高是( )
2.如图,两个正方形的面积分别为64,49,则AC=( )
A
C
64
49
B
A
B
C
13cm
60/13cm
17
D
3.以直角三角形的两直角边所作正方形的面积分别是25和144,则斜边长是( )
13
25
144
?
4.如图,分别以直角三角形三边为半径作半圆,则这三个半圆A,B,C的面积之间的关系( )
SA+SB=SC
D
A
B
C
a
b
c
5.若以直角三角形三边为边向外作正三角形呢?
勾股定理与面积
1.直角三角形的斜边上的高线AD=
A
B
C
D
AB×AC
BC
2.以直角三角形的三边向外作正方形、半圆、正三角形等,两直角边向外所作的图形面积和等于斜边向外所作的图形面积。
二.方程思想
1.在直角三角形中,∠C为直角,已知a:b=5:12,c=6.5,求a,b.
A
B
C
2.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,求旗杆的断裂处离地面的距离。
A
B
C
三.展开思想
1.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
10
20
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1.CF 2.EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
B
C
D
E
F
8
10
10
X
8-X
8-X
6
4
解:由题意得AD= BC=10CM
∴BF2=AF2-AB2=102-82
在直角三角形EFC中FC2+EC2=EF2
解,得 X=3
∴BF=6 FC=4
∵AB⊥BC
设EC=X,则EF=8-X。
即42+X2=(8-X)2
∴EC=3
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
三.展开思想
四.分类思想
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求(1)BD (2)CD (3)BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=
25
或7
A
B
C
分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
一.勾股定理与面积
1.直角三角形的斜边上的高线AD=
A
B
C
D
AB×AC
BC
2.以直角三角形的三边向外作正方形、半圆、正三角形两直角边向外所作的图形面积和等于斜边向外所作的图形面积。
二.方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.并利用两点之间线段最短,及勾股定理求解。
三.展开思想
四.分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
已知三角形ABC中,AB=10,BC=21,AC=17,求BC边上的高线AD。
A
B
C
D
解:设BD=X,则DC=21-X。
∵AD⊥BC
∴AD2=AB2-BD2=102-X2
AD2=AC2-CD2=172-(21-X)2
解,得 X=6
∴102-X2=172-(21-X)2
∴AD2=102-62=64
∴AD=8
再 见!
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
分割成若干个直角边为整数的三角形
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
把C看成边长为6的正方形面积的一半
C
A
B
A
B
C
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
图1-1
图1-2
∟
a
b
c
用四个全等的三角形拼一拼、摆一摆,看看能否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?
大正方形的面积可以表示为 ——————————
又可以表示为:———————
(a+b)
c2+1/2ab 4
a2 + b2 = c2
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
∟
a
b
c
大正方形的面积可以表示为 ——————————
又可以表示为:———————
∟
a
b
c
c
(b-a) +1/2ab 4
a2 + b2 = c2
3.已知一个Rt△的两边长分别为3和4,
则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
2.下列各组数中,以a,b,c为边的三角形
不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5
④若a∶b=3∶4,c=10,
则Rt△ABC的面积为________。
②若a=15,c=25,则b=___________;
1.在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
③若c=61,b=60,则a=__________;
13
20
11
24
A
D
4.以直角三角形的两直角边所作正方形的面积
分别是25和144,则斜边长是( )
5.如图,两个正方形的面积
分别为64,49,则AC=( )
A
D
C
64
C
64
49
6.三角形的三边长为(a+b)2=c2+2ab,则这个三角形是( )
A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.
13
17
C
7.果汁饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
A
C
B
5
12
13
1)郑凯想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
2)如图,厉俊杰家有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。请你算出他家这块地的面积。
A
C
B
D
C
A
D
B
3m
12m
4m
13m
3)如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
4)如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
亲爱的同学,通过今天的复习,对“勾股定理”的知识还有疑惑吗?
印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”,请用学过的数学知识回答这个问题。
2
X+0.5
X
C
B
A
已知Rt△ABC中,∠C=90°,
若a+b=14cm,c=10cm,
求Rt△ABC的面积.
