2.7、二次函数与一元二次方程
图片预览




文档简介
(共19张PPT)
2.7、二次函数与一元二次方程
济宁十二中 陈伟利
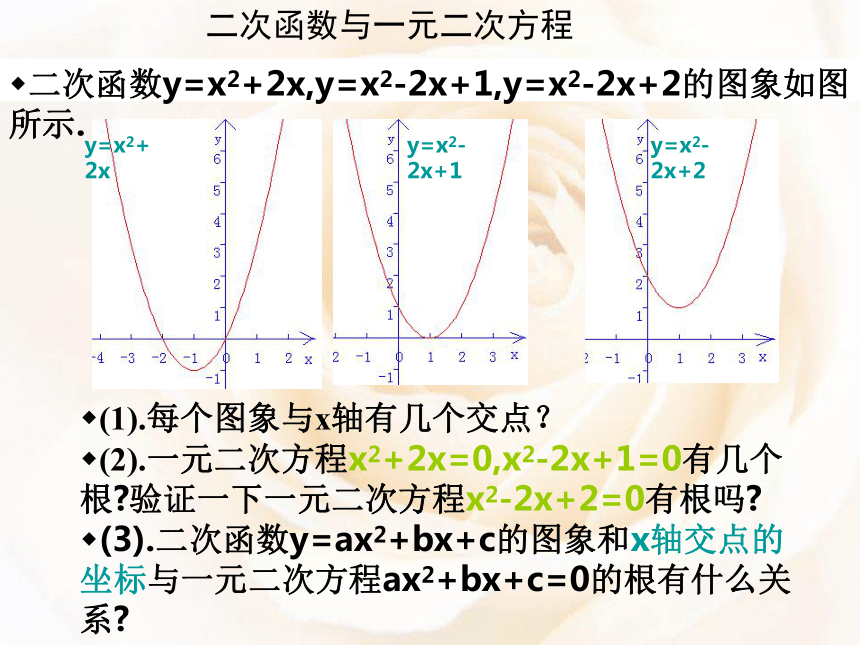
(1).每个图象与x轴有几个交点?
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数与一元二次方程
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.
y=x2+2x
y=x2-2x+1
y=x2-2x+2
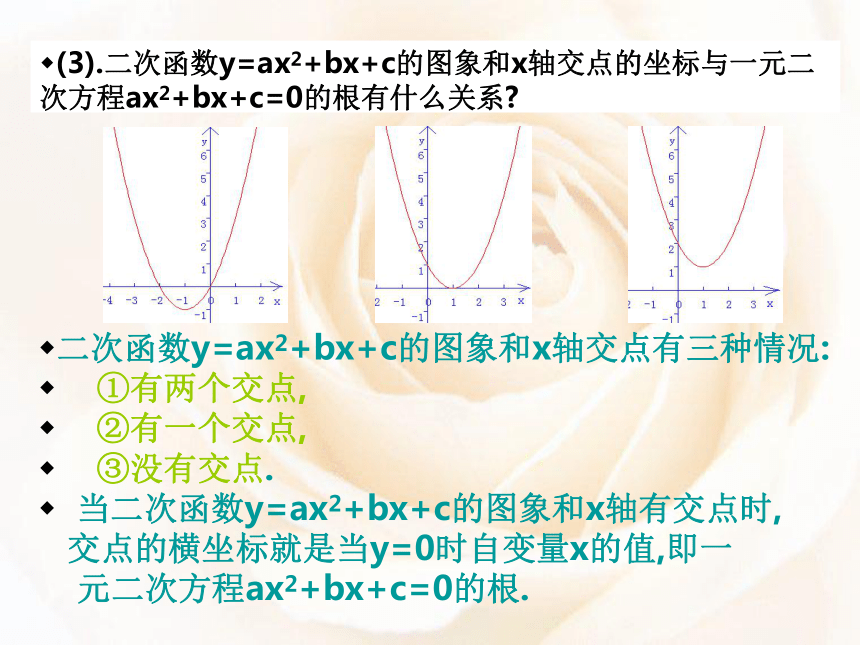
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
一、探究
探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)
你发现方程 的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0
点燃智慧的火花
结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。
即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )
x1,0
x2,0
x
O
A
B
x1
x2
y
开启 智慧
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
开启 智慧
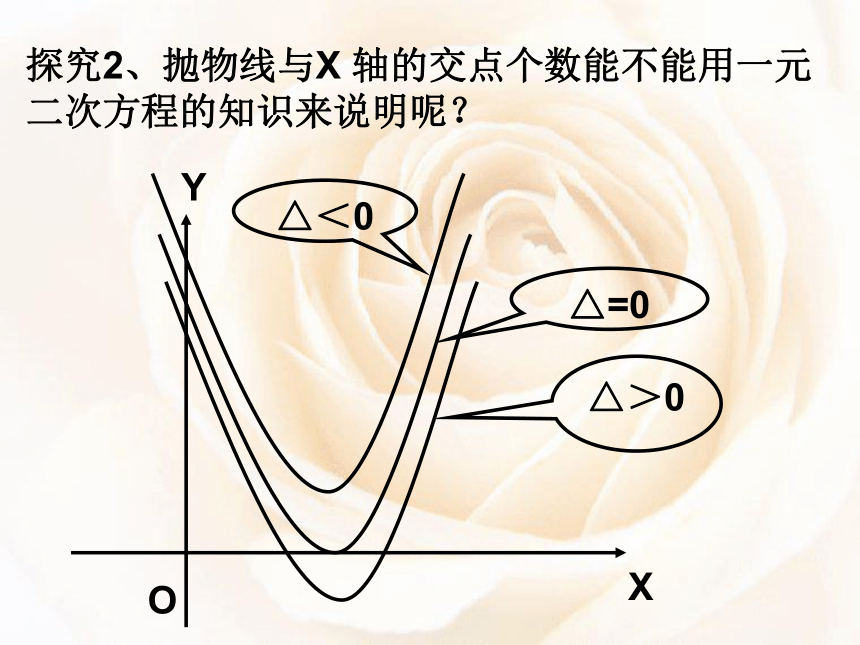
探究2、抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?
△>0
△=0
△<0
O
X
Y
结论2:
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、△>0 一元二次方程ax2+bx+c=0
有两个不等的实数根
与x轴有两个交点——相交。
抛物线y=ax2+bx+c
2、△=0 一元二次方程ax2+bx+c=0
有两个相等的实数根
与x轴有唯一公共点——相切(顶点)。
抛物线y=ax2+bx+c
3、△<0 一元二次方程ax2+bx+c=0
没有实数根
与x轴没有公共点——相离。
二、基础训练
1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;
3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。
2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。
独立
作业
评:若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),利用根与系数的关系,求证:A、B两点间的距离
AB=
4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+4
5. 已知抛物线 ,①求抛物线与y轴的交点坐标;②求抛物线与x轴的两个交点间的距离.
6、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0
D
7.已知二次函数y=-ax2,下列说法不正确的是( )
A.当a>0,x≠0时,y总取负值
B.当a<0,x<0时,y随x的增大而减小
C.当a<0时,函数图象有最低点,即y有最小值
D.当x<0,y= -ax2的对称轴是y轴
D
三、例题精讲
1、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,
求m的值。
提示:(1)⊿=4-4(m+1)=0
注:本题也可问当此抛物线顶点在x轴上时,求m的值。
(2)即方程x2+2x+m+1=x+2m的根只有一个。
2、已知抛物线y=-x2+2(m+1)x+m+3与x轴有两个交点A、B,其中A在x轴的正半轴,B在x轴的负半轴,
1)若OA=3OB,求m的值。
2)若3(OA-OB)=2OA·OB,求m的值。
例题精讲
学以致用右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
1、求抛物线
的解析式.
2、求两盏景观灯之
间的水平距离.
5
1
10
5m
1m
10m
A
B
C
D
4
注意知识的联系哦
学以致用
已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)k为何值时,二次函数y=x2-kx-2+k与轴两个交点A、B之间的距离最小?
(3)设此抛物线与y轴的交点为C,当k为6时,求S△ABC .
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。
3、A、B两点间的距离AB= 。
4、二次函数y=ax2+bx+c何时为一元二次方程 它们的关系如何
小结 拓展
驶向胜利的彼岸
课后探究
校运会上,某运动员掷铅球,铅球的高y(m)与水平距离x(m)之间的函数关系式为y=-0.2x2+2x+1.7,则此运动员的成绩是多少?
网址:http:///chenmo536
2.7、二次函数与一元二次方程
济宁十二中 陈伟利
(1).每个图象与x轴有几个交点?
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数与一元二次方程
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.
y=x2+2x
y=x2-2x+1
y=x2-2x+2
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
一、探究
探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)
你发现方程 的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0
点燃智慧的火花
结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。
即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )
x1,0
x2,0
x
O
A
B
x1
x2
y
开启 智慧
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
开启 智慧
探究2、抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?
△>0
△=0
△<0
O
X
Y
结论2:
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、△>0 一元二次方程ax2+bx+c=0
有两个不等的实数根
与x轴有两个交点——相交。
抛物线y=ax2+bx+c
2、△=0 一元二次方程ax2+bx+c=0
有两个相等的实数根
与x轴有唯一公共点——相切(顶点)。
抛物线y=ax2+bx+c
3、△<0 一元二次方程ax2+bx+c=0
没有实数根
与x轴没有公共点——相离。
二、基础训练
1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;
3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。
2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。
独立
作业
评:若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( x1,0 ), B(x2,0 ),利用根与系数的关系,求证:A、B两点间的距离
AB=
4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+4
5. 已知抛物线 ,①求抛物线与y轴的交点坐标;②求抛物线与x轴的两个交点间的距离.
6、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0
D
7.已知二次函数y=-ax2,下列说法不正确的是( )
A.当a>0,x≠0时,y总取负值
B.当a<0,x<0时,y随x的增大而减小
C.当a<0时,函数图象有最低点,即y有最小值
D.当x<0,y= -ax2的对称轴是y轴
D
三、例题精讲
1、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,
求m的值。
提示:(1)⊿=4-4(m+1)=0
注:本题也可问当此抛物线顶点在x轴上时,求m的值。
(2)即方程x2+2x+m+1=x+2m的根只有一个。
2、已知抛物线y=-x2+2(m+1)x+m+3与x轴有两个交点A、B,其中A在x轴的正半轴,B在x轴的负半轴,
1)若OA=3OB,求m的值。
2)若3(OA-OB)=2OA·OB,求m的值。
例题精讲
学以致用右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
1、求抛物线
的解析式.
2、求两盏景观灯之
间的水平距离.
5
1
10
5m
1m
10m
A
B
C
D
4
注意知识的联系哦
学以致用
已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)k为何值时,二次函数y=x2-kx-2+k与轴两个交点A、B之间的距离最小?
(3)设此抛物线与y轴的交点为C,当k为6时,求S△ABC .
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。
3、A、B两点间的距离AB= 。
4、二次函数y=ax2+bx+c何时为一元二次方程 它们的关系如何
小结 拓展
驶向胜利的彼岸
课后探究
校运会上,某运动员掷铅球,铅球的高y(m)与水平距离x(m)之间的函数关系式为y=-0.2x2+2x+1.7,则此运动员的成绩是多少?
网址:http:///chenmo536
