2.5、用三种方式表示二次函数.
图片预览


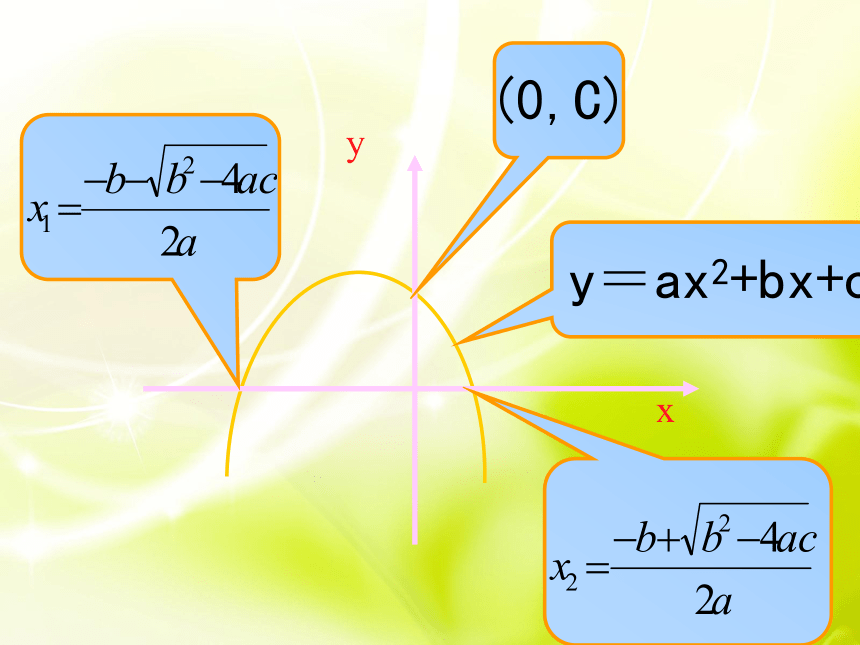



文档简介
(共20张PPT)
九年级数学(上) 第二章 二次函数
----用三种方式表示二次函数
济宁十二中 陈伟利
1、二次函数y=ax2+bx+c
配方得:
顶点是:
对称轴:
一元二次方程求根公式:
x
y
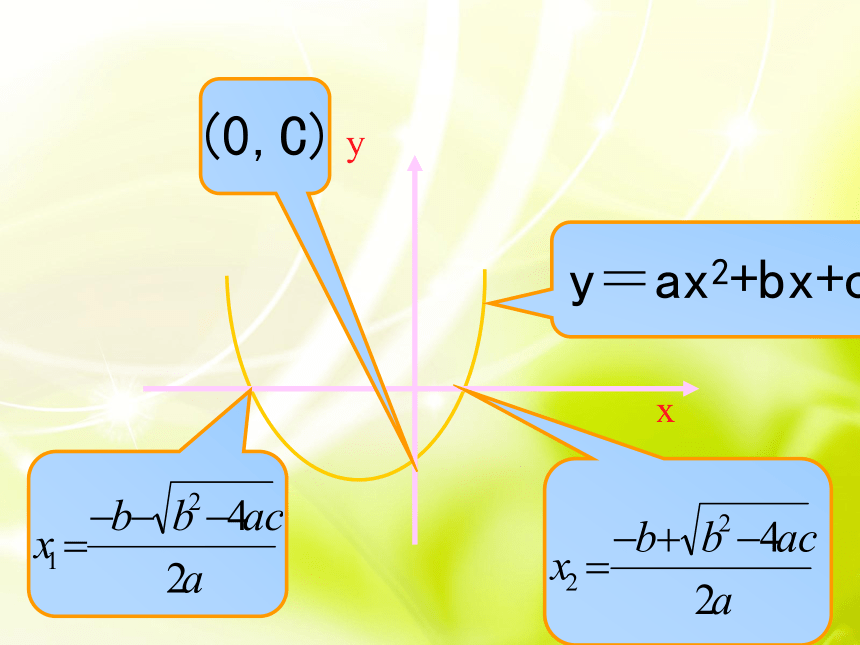
y=ax2+bx+c
(0,C)
x
y
y=ax2+bx+c
(0,C)
x
y
(1,0)
(-5,0)
(0,-1)
1、函数 对称轴是 ;
顶点坐标是 ;
2、求下列函数的顶点坐标、对称轴。
一、课前一测
(1)
(2)
注意:画二次函数图象要注意如下技巧:
(1)先找到对称轴、顶点坐标;
(2)取“5个点”绘出图象,
这5点一定包括:
例1、画出 的图象。
二、新课探究
例2、作出 的图象。
五点
x轴的交点坐标(两个)
与y轴的交点(一个)及其对称的点(一个)
顶点(一个)
例3:一名同学推铅球时,铅球行进中离地的高度y(m)与水平距离x(m)之间的关系可
以用 的函数关系来描述。
(1)求铅球最高达到多高?
(2)作出函数图象。并根据图象说明:
铅球行进中x(m)在什么范围内离地面越来越远?铅球最远有多远?
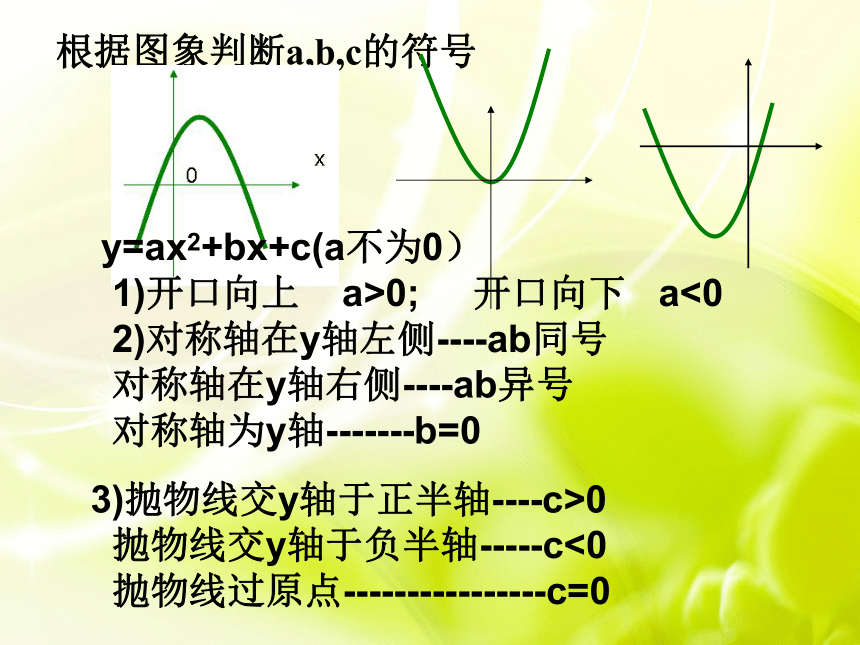
根据图象判断a,b,c的符号
y=ax2+bx+c(a不为0) 1)开口向上 a>0; 开口向下 a<0 2)对称轴在y轴左侧----ab同号 对称轴在y轴右侧----ab异号 对称轴为y轴-------b=0
3)抛物线交y轴于正半轴----c>0 抛物线交y轴于负半轴-----c<0 抛物线过原点----------------c=0
①图象开口向上:a>0,图象开口向下:a<0,
②图象与y轴正半轴有交点:c>0,
图象与y轴负半轴有交点:c<0
图象过原点:c=0
③对称轴在y轴右側:a,b异号;
对称轴在y轴左側:a,b同号。
对称轴为y轴: b =0
④图象与x轴有两个交点:b2-4ac >0;
图象与x轴有1个交点:b2-4ac =0;
图象与x轴无交点:b2-4ac < 0;
⑤图象与x轴交点已知:可以判断ax2+bx+c=0的根
⑥x轴有横坐标n:可以判断an2+bn+c的符号。
识图规律
o
x
y
a<0
b<0
c>0
b2-4ac > 0
1
填空:
a___0; b____0
c___0 a+b+c___0
a-b+c___0
-1
y=ax2+bx+c
o
x
y
2
1
-1
例4:已知二次函数y=ax2+bx+c
(a≠0)的图象,则
(1) a 0; (2) b 0;
(3) c 0;
(4) a+b+c 0;
(5) a-b+c 0;
(6) b2 - 4ac 0;
(7) 2a+b 0; (8) 4a+2b+c 0;
<
>
<
>
<
>
>
=
(3)在同一直角坐标系中,函数y=ax2+b、y=ax+b(ab≠0)
的图象大致如图 ( )
y
y
y
y
x
x
x
x
O
O
O
O
A
B
C
D
D
(2)直线y=ax+b(ab≠0)不过第三象限,那么函数
y=ax2+bx的图象大致如图 ( )
B
A B C D
1. 一次函数y=ax+b与y=ax2-b在同一坐标系中的大致图象是( )
思维与拓展
x
0
y
x
0
x
0
x
0
x
x
y
y
y
B.
A.
C.
D.
B
2. 函数y=ax2+a与y= (a≠0)在同一坐标系中 的大致图象是( )
思维与拓展
y
x
0
x
0
y
x
0
y
A.
x
y
0
B.
C.
D.
D.
三、二次函数解析式的求法
(1)一般式 y=ax2+bx+c
(2) 顶点式 y=a(x-h)2+k
有三个系数a,b,c故需三个点坐标.
例:抛物线过A(-1,0), (1,-4),(0,-3),求抛物线解析式
需两点,其中一点是顶点.
例:过A(-1,0)的抛物线的顶点是(2,3),求 抛物线的解析式
解析式最后都要用一般式表示
三、二次函数解析式的求法:
(3)通过看图确定解释式;
解析式最后都要用一般式表示
(2,4)
(2,5)
1
-2
(-3,4)
2
-4
(3,7)
解:设
解:设
解:设
解:建立如图所示的坐标系
例.一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少 (结果精确到0.1m).
●A(2,-2)
●B(X,-3)
三、拓展训练:
变式训练:如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽为20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.
(1)在如图的坐标系中求出此抛物线的表达式;
(2)若洪水到来时,水位以每小时0.2米的速度上升,从正常水位开始,再持续多长时间,会达到共拱顶
x
y
o
C
D
A
B
九年级数学(上) 第二章 二次函数
----用三种方式表示二次函数
济宁十二中 陈伟利
1、二次函数y=ax2+bx+c
配方得:
顶点是:
对称轴:
一元二次方程求根公式:
x
y
y=ax2+bx+c
(0,C)
x
y
y=ax2+bx+c
(0,C)
x
y
(1,0)
(-5,0)
(0,-1)
1、函数 对称轴是 ;
顶点坐标是 ;
2、求下列函数的顶点坐标、对称轴。
一、课前一测
(1)
(2)
注意:画二次函数图象要注意如下技巧:
(1)先找到对称轴、顶点坐标;
(2)取“5个点”绘出图象,
这5点一定包括:
例1、画出 的图象。
二、新课探究
例2、作出 的图象。
五点
x轴的交点坐标(两个)
与y轴的交点(一个)及其对称的点(一个)
顶点(一个)
例3:一名同学推铅球时,铅球行进中离地的高度y(m)与水平距离x(m)之间的关系可
以用 的函数关系来描述。
(1)求铅球最高达到多高?
(2)作出函数图象。并根据图象说明:
铅球行进中x(m)在什么范围内离地面越来越远?铅球最远有多远?
根据图象判断a,b,c的符号
y=ax2+bx+c(a不为0) 1)开口向上 a>0; 开口向下 a<0 2)对称轴在y轴左侧----ab同号 对称轴在y轴右侧----ab异号 对称轴为y轴-------b=0
3)抛物线交y轴于正半轴----c>0 抛物线交y轴于负半轴-----c<0 抛物线过原点----------------c=0
①图象开口向上:a>0,图象开口向下:a<0,
②图象与y轴正半轴有交点:c>0,
图象与y轴负半轴有交点:c<0
图象过原点:c=0
③对称轴在y轴右側:a,b异号;
对称轴在y轴左側:a,b同号。
对称轴为y轴: b =0
④图象与x轴有两个交点:b2-4ac >0;
图象与x轴有1个交点:b2-4ac =0;
图象与x轴无交点:b2-4ac < 0;
⑤图象与x轴交点已知:可以判断ax2+bx+c=0的根
⑥x轴有横坐标n:可以判断an2+bn+c的符号。
识图规律
o
x
y
a<0
b<0
c>0
b2-4ac > 0
1
填空:
a___0; b____0
c___0 a+b+c___0
a-b+c___0
-1
y=ax2+bx+c
o
x
y
2
1
-1
例4:已知二次函数y=ax2+bx+c
(a≠0)的图象,则
(1) a 0; (2) b 0;
(3) c 0;
(4) a+b+c 0;
(5) a-b+c 0;
(6) b2 - 4ac 0;
(7) 2a+b 0; (8) 4a+2b+c 0;
<
>
<
>
<
>
>
=
(3)在同一直角坐标系中,函数y=ax2+b、y=ax+b(ab≠0)
的图象大致如图 ( )
y
y
y
y
x
x
x
x
O
O
O
O
A
B
C
D
D
(2)直线y=ax+b(ab≠0)不过第三象限,那么函数
y=ax2+bx的图象大致如图 ( )
B
A B C D
1. 一次函数y=ax+b与y=ax2-b在同一坐标系中的大致图象是( )
思维与拓展
x
0
y
x
0
x
0
x
0
x
x
y
y
y
B.
A.
C.
D.
B
2. 函数y=ax2+a与y= (a≠0)在同一坐标系中 的大致图象是( )
思维与拓展
y
x
0
x
0
y
x
0
y
A.
x
y
0
B.
C.
D.
D.
三、二次函数解析式的求法
(1)一般式 y=ax2+bx+c
(2) 顶点式 y=a(x-h)2+k
有三个系数a,b,c故需三个点坐标.
例:抛物线过A(-1,0), (1,-4),(0,-3),求抛物线解析式
需两点,其中一点是顶点.
例:过A(-1,0)的抛物线的顶点是(2,3),求 抛物线的解析式
解析式最后都要用一般式表示
三、二次函数解析式的求法:
(3)通过看图确定解释式;
解析式最后都要用一般式表示
(2,4)
(2,5)
1
-2
(-3,4)
2
-4
(3,7)
解:设
解:设
解:设
解:建立如图所示的坐标系
例.一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少 (结果精确到0.1m).
●A(2,-2)
●B(X,-3)
三、拓展训练:
变式训练:如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽为20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.
(1)在如图的坐标系中求出此抛物线的表达式;
(2)若洪水到来时,水位以每小时0.2米的速度上升,从正常水位开始,再持续多长时间,会达到共拱顶
x
y
o
C
D
A
B
