人教A版必修5第三章3.4.1基本不等式 课件(共16张PPT)
文档属性
| 名称 | 人教A版必修5第三章3.4.1基本不等式 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 21.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 16:22:14 | ||
图片预览





文档简介
(共16张PPT)
3.4
基本不等式:
人教A版数学必修5
第三章
不等式
(第一课时)
1.如果矩形菜园的面积为100m2,为节省材料,就应该考虑所用篱笆最
的问题.
最大是
m2;
最短是
m;
情境1:陶渊明为防止家畜家禽对菜地的破坏,打算用篱笆围成一个菜园.
2.如果用一段长为36m的篱笆围成矩形菜园,为了充分利用材料,就要考虑所围菜园面积最
的问题.
一、情境创设
导入课题
短
大
?
?
一、情境创设
导入课题
情境2:请看一段视频,并观察下面这个图形在视频中出现了几次?
一、情境创设
导入课题
一、情境创设
导入课题
情境2:这个图形在视频中出现了3次.你见过这个图形吗?
第24届国际数学家大会(ICM2002)的会标
(3)
=
(2)
=
(1)正方形
的边长为
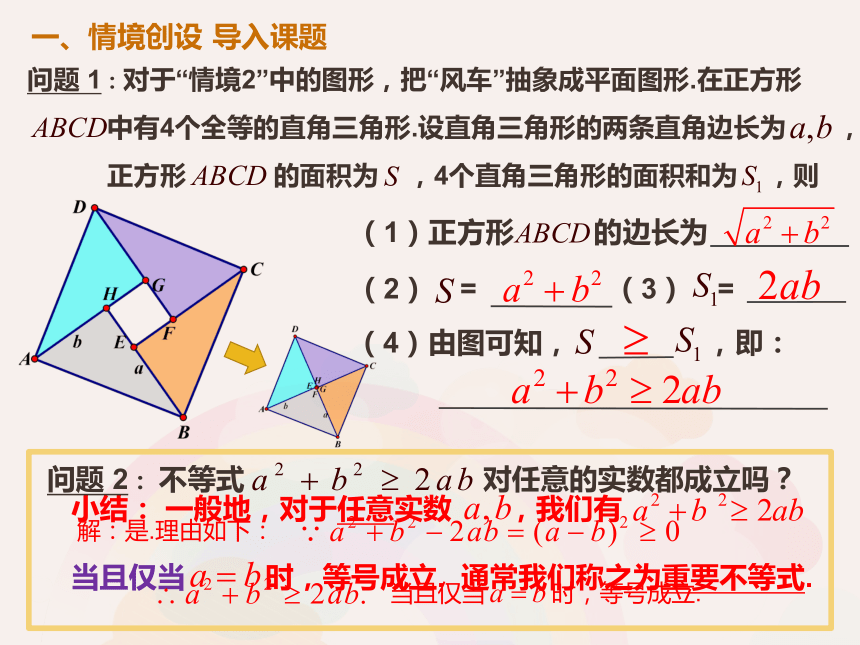
问题
1:对于“情境2”中的图形,把“风车”抽象成平面图形.在正方形
中有4个全等的直角三角形.设直角三角形的两条直角边长为
,
正方形
的面积为
,4个直角三角形的面积和为
,则
(4)由图可知,
,即:
小结:
一般地,对于任意实数
,我们有
当且仅当
时,等号成立.
通常我们称之为重要不等式.
问题
2:
不等式
对任意的实数都成立吗?
当且仅当
时,等号成立.
解:是.理由如下:
一、情境创设
导入课题
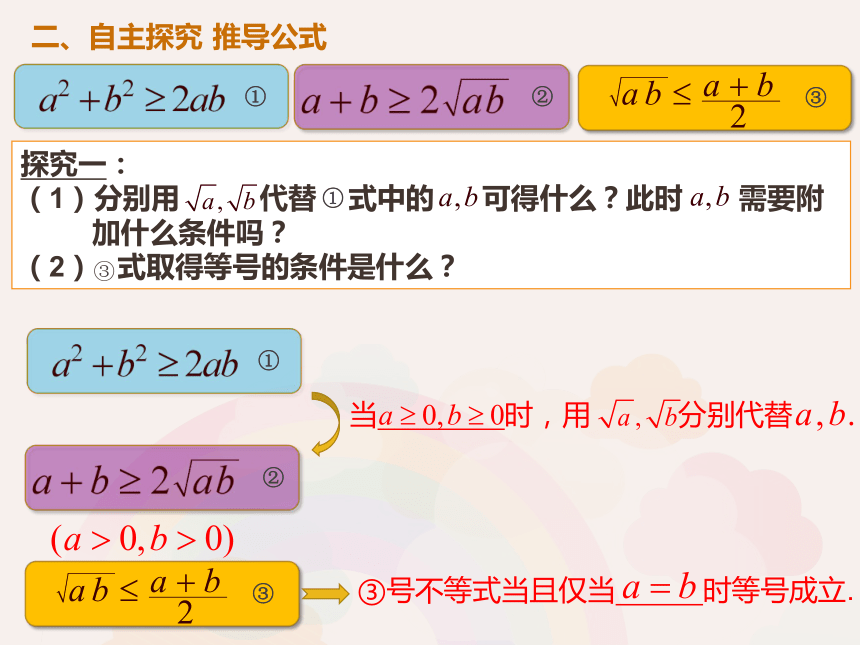
①
②
③
当
时,用
分别代替
①
②
③
探究一:
(1)分别用
代替
式中的
可得什么?此时
需要附
加什么条件吗?
(2)
式取得等号的条件是什么?
①
③号不等式当且仅当
时等号成立.
二、自主探究
推导公式
③
要证
①
只要证
②
要证②,
只要证
③
要证③,
只要证
④
显然,④是成立的.当且仅当
时,④中的等号成立.
小结:如果
那么
,
通常我们称之为
基本不等式.
当且仅当
时,等号成立.
①
②
③
二、自主探究
推导公式
问题
3:能否利用不等式的性质,直接推导出
?我们来分析一下.
正数
的算术平均数不小于它们的几何平均数
基本不等式的几何意义:
半径不小于弦长的一半
探究二:如图,
是圆的直径,点
是
上一点,
,
.
过点
作垂直于
的弦
,
连接
,
.
用含
的代数式填空.
(1)半径
(2)
(3)显然
二、自主探究
推导公式
(2)把
写成两个正数的和,当这两个正数取什么值时,
它们的积最大?
(1)把
写成两个正数的积,当这两个正数取什么值时,
它们的和最小?
例1
归纳小结
利用基本不等式求最值:对于两个正实数
如果它们的积
是定值,当且仅当
时,它们的和
取得最小值.(积定和最小)
如果它们的和
是定值,当且仅当
时,它们的积
取得最大值.(和定积最大)
三、巩固强化
深化认识
函数
的最小值为
(
)
若
且
则
(
)
函数
的最小值为
(
)
强化训练:判断下列3个命题是否正确,请简单说理.
注意:利用基本不等式求最值时:“一正二定三相等”
三、巩固强化
深化认识
背景材料:陶渊明为防止家畜家禽对菜地的破坏,打算用篱笆围成一个菜园.如果菜园的面积一定,为节省材料,就应该考虑所用篱笆最短的问题;如果所用篱笆的长度一定,为了充分利用材料,就要考虑所围菜园面积最大的问题.
例2
(1)用篱笆围一个面积为
的矩形菜园,问这个矩
形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少?
(2)一段长为
的篱笆围成一个矩形菜园,问这个矩形
的长、宽各为多少时,菜园的面积最大.最大面积是多少?
四、实际应用
升华理解
(1)正确理解题意,设出变量,一般可以把要求最大(小)
值的变量定为函数;
(2)建立相应的函数关系式,把实际问题抽象成求函数的
最大值或最小值问题;
(3)在定义域内,求出函数的最大值或最小值;
(4)正确写出答案.
本题小结:利用基本不等式解决实际问题的一般步骤:
四、实际应用
升华理解
情境1:陶渊明为防止家畜家禽对菜地的破坏,打算用篱笆围成一个菜园.
1.如果矩形菜园的面积为100m2,为节省材料,就应该考虑所用篱笆最短的问题,最短是
40
m;
2.如果用一段长为36m的篱笆围成矩形菜园,为了充分利用材料,就要考虑所围菜园面积最大的问题,最大是
81
m2;
情境再现:
六、课堂小结
布置作业
数学抽象
直观想象
数形结合
分类
代换
逻辑推理
当且仅当
时等号成立.
掌握
特殊到一般
化归与转化
两个正数
和定积最大
积定和最小
两数相等取最值
数学运算
数学建模
数形结合
应用
变形
……
注意:一正二定三相等!!
1、阅读课本97-100页;
2、课本100页练习2、3;
3、思考题(选做):水管为什么做成圆柱形?
六、课堂小结
布置作业
鹿邑县高中
徐志华
感谢各位领导及老师的聆听!
同学们,
加油哦!
拓展提高:
1、若
求
的最大值.
3.4
基本不等式:
人教A版数学必修5
第三章
不等式
(第一课时)
1.如果矩形菜园的面积为100m2,为节省材料,就应该考虑所用篱笆最
的问题.
最大是
m2;
最短是
m;
情境1:陶渊明为防止家畜家禽对菜地的破坏,打算用篱笆围成一个菜园.
2.如果用一段长为36m的篱笆围成矩形菜园,为了充分利用材料,就要考虑所围菜园面积最
的问题.
一、情境创设
导入课题
短
大
?
?
一、情境创设
导入课题
情境2:请看一段视频,并观察下面这个图形在视频中出现了几次?
一、情境创设
导入课题
一、情境创设
导入课题
情境2:这个图形在视频中出现了3次.你见过这个图形吗?
第24届国际数学家大会(ICM2002)的会标
(3)
=
(2)
=
(1)正方形
的边长为
问题
1:对于“情境2”中的图形,把“风车”抽象成平面图形.在正方形
中有4个全等的直角三角形.设直角三角形的两条直角边长为
,
正方形
的面积为
,4个直角三角形的面积和为
,则
(4)由图可知,
,即:
小结:
一般地,对于任意实数
,我们有
当且仅当
时,等号成立.
通常我们称之为重要不等式.
问题
2:
不等式
对任意的实数都成立吗?
当且仅当
时,等号成立.
解:是.理由如下:
一、情境创设
导入课题
①
②
③
当
时,用
分别代替
①
②
③
探究一:
(1)分别用
代替
式中的
可得什么?此时
需要附
加什么条件吗?
(2)
式取得等号的条件是什么?
①
③号不等式当且仅当
时等号成立.
二、自主探究
推导公式
③
要证
①
只要证
②
要证②,
只要证
③
要证③,
只要证
④
显然,④是成立的.当且仅当
时,④中的等号成立.
小结:如果
那么
,
通常我们称之为
基本不等式.
当且仅当
时,等号成立.
①
②
③
二、自主探究
推导公式
问题
3:能否利用不等式的性质,直接推导出
?我们来分析一下.
正数
的算术平均数不小于它们的几何平均数
基本不等式的几何意义:
半径不小于弦长的一半
探究二:如图,
是圆的直径,点
是
上一点,
,
.
过点
作垂直于
的弦
,
连接
,
.
用含
的代数式填空.
(1)半径
(2)
(3)显然
二、自主探究
推导公式
(2)把
写成两个正数的和,当这两个正数取什么值时,
它们的积最大?
(1)把
写成两个正数的积,当这两个正数取什么值时,
它们的和最小?
例1
归纳小结
利用基本不等式求最值:对于两个正实数
如果它们的积
是定值,当且仅当
时,它们的和
取得最小值.(积定和最小)
如果它们的和
是定值,当且仅当
时,它们的积
取得最大值.(和定积最大)
三、巩固强化
深化认识
函数
的最小值为
(
)
若
且
则
(
)
函数
的最小值为
(
)
强化训练:判断下列3个命题是否正确,请简单说理.
注意:利用基本不等式求最值时:“一正二定三相等”
三、巩固强化
深化认识
背景材料:陶渊明为防止家畜家禽对菜地的破坏,打算用篱笆围成一个菜园.如果菜园的面积一定,为节省材料,就应该考虑所用篱笆最短的问题;如果所用篱笆的长度一定,为了充分利用材料,就要考虑所围菜园面积最大的问题.
例2
(1)用篱笆围一个面积为
的矩形菜园,问这个矩
形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少?
(2)一段长为
的篱笆围成一个矩形菜园,问这个矩形
的长、宽各为多少时,菜园的面积最大.最大面积是多少?
四、实际应用
升华理解
(1)正确理解题意,设出变量,一般可以把要求最大(小)
值的变量定为函数;
(2)建立相应的函数关系式,把实际问题抽象成求函数的
最大值或最小值问题;
(3)在定义域内,求出函数的最大值或最小值;
(4)正确写出答案.
本题小结:利用基本不等式解决实际问题的一般步骤:
四、实际应用
升华理解
情境1:陶渊明为防止家畜家禽对菜地的破坏,打算用篱笆围成一个菜园.
1.如果矩形菜园的面积为100m2,为节省材料,就应该考虑所用篱笆最短的问题,最短是
40
m;
2.如果用一段长为36m的篱笆围成矩形菜园,为了充分利用材料,就要考虑所围菜园面积最大的问题,最大是
81
m2;
情境再现:
六、课堂小结
布置作业
数学抽象
直观想象
数形结合
分类
代换
逻辑推理
当且仅当
时等号成立.
掌握
特殊到一般
化归与转化
两个正数
和定积最大
积定和最小
两数相等取最值
数学运算
数学建模
数形结合
应用
变形
……
注意:一正二定三相等!!
1、阅读课本97-100页;
2、课本100页练习2、3;
3、思考题(选做):水管为什么做成圆柱形?
六、课堂小结
布置作业
鹿邑县高中
徐志华
感谢各位领导及老师的聆听!
同学们,
加油哦!
拓展提高:
1、若
求
的最大值.
