五年级上册数学课件5.2.4实际问题与方程-例2 人教版 (共25张PPT)
文档属性
| 名称 | 五年级上册数学课件5.2.4实际问题与方程-例2 人教版 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
简易方程
实际问题与方程
例2
1、会解较复杂的方程。
2、进一步掌握列方程解决问题的方法。
学习目标:
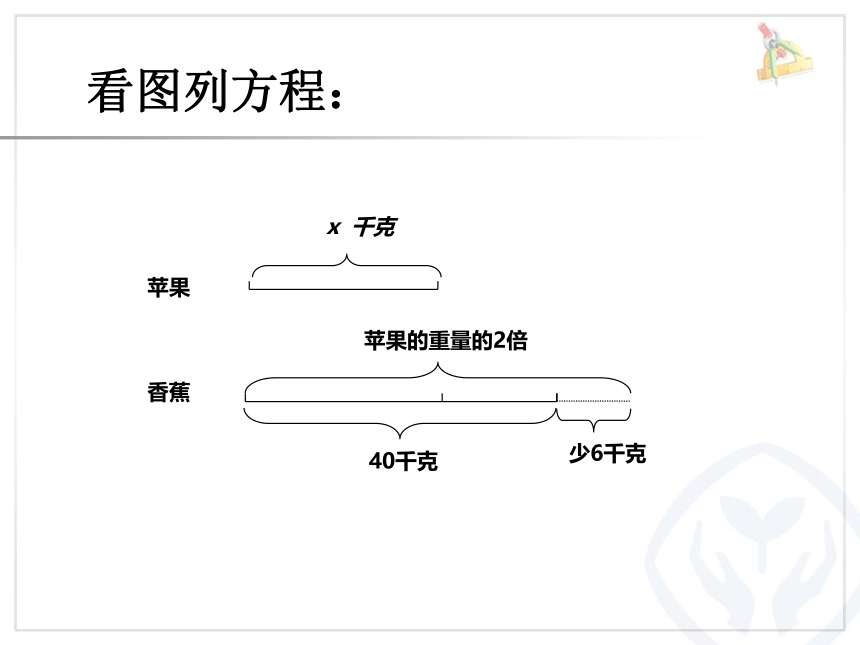
少6千克
40千克
苹果
香蕉
苹果的重量的2倍
x
千克
看图列方程:
复习:
1.先说说下面各题的数量关系,再列方程,不用求解。
(1)公鸡x
只,母鸡30只,比公鸡只数少6只。
(2)公鸡x
只,母鸡30只,是公鸡只数的2倍。
找出下面各题的等量关系式。
故事书的本数比文艺书的3倍还多50本。
爸爸的年龄比小明的4倍小8岁。
一本书,看了的页数比剩下页数的2倍少10页。
苹果的筐数比梨的2.4倍多12筐。
不得已流浪在外,
被追逐处处难待,
偶然能逃进门来,
却又被一脚踢开。
(打一体育运动)
令无数人着迷的足球
一、复习导入
1、足球上黑色皮共有12块,白色皮比黑色皮
的2倍少4块,足球上白色皮有多少块?
(只列式不计算)
列式:______
12
×2-4
问题:从图中得到了哪些数学信息?
一、创设情境
激发兴趣
(五边形、六边形与所要解决的问题没有关系,是多余条件)
已知条件:①白色皮20块
②白色皮比黑色皮的2倍少4块。
所求问题:
黑色皮多少块?
二、合作交流
探究新知
(一)明确问题
提出要求
2.
像这样的题我们可以用列方程的方法,使逆向的问题变成顺向就简单了。如果再有困难,我们还可以画
线段图来帮助思考。
用算术方法做,只列式不计算,列式:________
问题:这道题同学们为什么做的这么慢呢?是什么原因?
二、合作交流
探究新知
4块
20块
黑色皮
白色皮
2x块
x块
线段示意图
4块
20块
黑色皮
白色皮
2x块
x块
二、合作交流
探究新知
根据题意及线段图列等量关系式
黑色皮的块数×2-4=白色皮的块数
黑色皮块数×2-白色皮块数=4
黑色皮块数×2=白色皮块数+4
解:设共有x块黑色皮。
共有多少块黑色皮?
用线段表示
少4块
20块
?块
用方程解答
黑色皮的块数×2-4=白色皮的块数
2x-4=20
2x-4+4=20+4
x=12
2x÷2=24÷2
2x=24
答:共有20块白皮球。
二、合作交流
探究新知
解:设共有x块黑色皮。
2x-4=20
解:设共有x块黑色皮。
2x-20=4
解:设共有x块黑色皮。
2x=20+4
(三)设未知数列方程并解方程
x=12
2x÷2=24÷2
2x=24
2x-4+4=20+4
x=12
2x÷2=24÷2
2x=24
x=12
2x÷2=24÷2
2x=24
2
x-20+20=4+20
黑色皮块数×2=白色皮块数+4
黑色皮块数×2-白色皮块数=4
黑色皮块数×2
-4=白色皮块数
1.
仔细观察解方程的过程,它们有什么共同的特点?
(都是先把2x看作一个整体,先求2x等于多少,再求x等于多少;且最终都转化成2x=24的形式,)
4.怎么检验这道题是否正确?
3.
解决同一个问题,我们根据等量关系式列出了三个不同的方程,如果把
其中一个看做主体的话,那么另两个就是它的变式。
2.化繁为简,化难为易,化新知为旧知,化未知为已知是数学常用的方法。
①弄清题意,设未知量为x。
刚才我们通过列方程解决了一个稍复杂的问题,你能说说列方程解决问题主要有哪些步骤吗?其中哪一个步骤是最关键的?
(五)总结提升
①
设
②分析题意,找等量关系。
②
找▲(关键)
③根据等量关系列出方程。
③
列
④解方程。
④解
⑤检验答案是不是方程的解。
⑤验答
共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
从题目中你还能找到什么样的等量关系式进行解答?
1、共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
每筒网球的个数×筒数+3=网球总数
解:设一共装了x筒。
答:一共装了285筒。
5x+3=1428
5x+3-3=1428-3
5x=1425
5x
÷
5=1425
÷
5
x=285
检验:
方程左边=5x+3
=5╳285+3
=1425+3
=1428
=方程右边
所以:x=285是所列方程的解。
2、根据方程列出等量关系式。
粮店运来72吨大米,比运来的面粉的3倍多12吨。运来面粉多少吨?
根据_______________________________________,
列方程:3x
+12=72。
根据_______________________________________,
列方程:72-3x
=12。
面粉的吨数╳3+12=大米的吨数(72吨)
大米的吨数(72吨)-面粉的吨数╳3=12
2.蓝鲸的寿命大约是100年。
海象的寿命大约是多少?
比海象的3倍少20年。
4.蓝鲸的寿命大约是100年。
比海象的3倍少20年。
海象的寿命大约是多少?
海象寿命×3-20=蓝鲸寿命
解:设海象的寿命大约是x年。
3x-20=100
3x-20+20=100+20
3x=120
3x÷3=120÷3
x
=
40
方程左边=3x-20
=3╳40-20
=120-20
=100
=方程右边
所以:x=
40是所列方程的解。
检验:
答:海象的寿命大约是40年。
3、先说说下列各题的数量关系,再列方程解决问题。
天安门广场的面积╳2-16=故宫的面积(72万m?)
解:设天安门广场的面积是x万平方米。
2x-16=72
2x-16+16=72+16
2
x
=
88
2x÷2=88÷2
x
=
44
方程左边=2x-16
=2╳44-16
=88-16
=722
=方程右边
所以:x=
44是所列方程的解。
检验:
答:天安门广场的面积是44万平方米。
故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。天安门广场的面积是多少万平方米?
用方程解答。
2.
一头大象的体重是4吨,比一头牛体重的4倍还多0.2吨。这头牛体重多少吨?
3.
四、总结质疑
反思评价
1.
今天这节课你有哪些收获?
2.这节课你学会了用什么方法来解决实际问题?
3.什么类型的题目适合用今天所学的方法来解答?
4.用这样的方法来解决实际问题时要注意什么?
作业
四、总结质疑
反思评价
1.
回顾一下,今天这节课你有哪些收获?
(1)已知标准量,求比较量,用算式方法解比较简单;逆向思维的问题
用方程解能使它变成顺向,降低难度,用方程解比较简单。
(2)把没有学过的方程转化成学过的方程,数学中很多地方都要用到这种方法,
化繁为简,化难为易,化新知为旧知。
(3)对于复杂的问题,我们可以画线段图,分析数量关系,理解题意。
(4)列方程解决问题要记住步骤,书写要规范,并自觉养成检验的习惯。
简易方程
实际问题与方程
例2
1、会解较复杂的方程。
2、进一步掌握列方程解决问题的方法。
学习目标:
少6千克
40千克
苹果
香蕉
苹果的重量的2倍
x
千克
看图列方程:
复习:
1.先说说下面各题的数量关系,再列方程,不用求解。
(1)公鸡x
只,母鸡30只,比公鸡只数少6只。
(2)公鸡x
只,母鸡30只,是公鸡只数的2倍。
找出下面各题的等量关系式。
故事书的本数比文艺书的3倍还多50本。
爸爸的年龄比小明的4倍小8岁。
一本书,看了的页数比剩下页数的2倍少10页。
苹果的筐数比梨的2.4倍多12筐。
不得已流浪在外,
被追逐处处难待,
偶然能逃进门来,
却又被一脚踢开。
(打一体育运动)
令无数人着迷的足球
一、复习导入
1、足球上黑色皮共有12块,白色皮比黑色皮
的2倍少4块,足球上白色皮有多少块?
(只列式不计算)
列式:______
12
×2-4
问题:从图中得到了哪些数学信息?
一、创设情境
激发兴趣
(五边形、六边形与所要解决的问题没有关系,是多余条件)
已知条件:①白色皮20块
②白色皮比黑色皮的2倍少4块。
所求问题:
黑色皮多少块?
二、合作交流
探究新知
(一)明确问题
提出要求
2.
像这样的题我们可以用列方程的方法,使逆向的问题变成顺向就简单了。如果再有困难,我们还可以画
线段图来帮助思考。
用算术方法做,只列式不计算,列式:________
问题:这道题同学们为什么做的这么慢呢?是什么原因?
二、合作交流
探究新知
4块
20块
黑色皮
白色皮
2x块
x块
线段示意图
4块
20块
黑色皮
白色皮
2x块
x块
二、合作交流
探究新知
根据题意及线段图列等量关系式
黑色皮的块数×2-4=白色皮的块数
黑色皮块数×2-白色皮块数=4
黑色皮块数×2=白色皮块数+4
解:设共有x块黑色皮。
共有多少块黑色皮?
用线段表示
少4块
20块
?块
用方程解答
黑色皮的块数×2-4=白色皮的块数
2x-4=20
2x-4+4=20+4
x=12
2x÷2=24÷2
2x=24
答:共有20块白皮球。
二、合作交流
探究新知
解:设共有x块黑色皮。
2x-4=20
解:设共有x块黑色皮。
2x-20=4
解:设共有x块黑色皮。
2x=20+4
(三)设未知数列方程并解方程
x=12
2x÷2=24÷2
2x=24
2x-4+4=20+4
x=12
2x÷2=24÷2
2x=24
x=12
2x÷2=24÷2
2x=24
2
x-20+20=4+20
黑色皮块数×2=白色皮块数+4
黑色皮块数×2-白色皮块数=4
黑色皮块数×2
-4=白色皮块数
1.
仔细观察解方程的过程,它们有什么共同的特点?
(都是先把2x看作一个整体,先求2x等于多少,再求x等于多少;且最终都转化成2x=24的形式,)
4.怎么检验这道题是否正确?
3.
解决同一个问题,我们根据等量关系式列出了三个不同的方程,如果把
其中一个看做主体的话,那么另两个就是它的变式。
2.化繁为简,化难为易,化新知为旧知,化未知为已知是数学常用的方法。
①弄清题意,设未知量为x。
刚才我们通过列方程解决了一个稍复杂的问题,你能说说列方程解决问题主要有哪些步骤吗?其中哪一个步骤是最关键的?
(五)总结提升
①
设
②分析题意,找等量关系。
②
找▲(关键)
③根据等量关系列出方程。
③
列
④解方程。
④解
⑤检验答案是不是方程的解。
⑤验答
共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
从题目中你还能找到什么样的等量关系式进行解答?
1、共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
每筒网球的个数×筒数+3=网球总数
解:设一共装了x筒。
答:一共装了285筒。
5x+3=1428
5x+3-3=1428-3
5x=1425
5x
÷
5=1425
÷
5
x=285
检验:
方程左边=5x+3
=5╳285+3
=1425+3
=1428
=方程右边
所以:x=285是所列方程的解。
2、根据方程列出等量关系式。
粮店运来72吨大米,比运来的面粉的3倍多12吨。运来面粉多少吨?
根据_______________________________________,
列方程:3x
+12=72。
根据_______________________________________,
列方程:72-3x
=12。
面粉的吨数╳3+12=大米的吨数(72吨)
大米的吨数(72吨)-面粉的吨数╳3=12
2.蓝鲸的寿命大约是100年。
海象的寿命大约是多少?
比海象的3倍少20年。
4.蓝鲸的寿命大约是100年。
比海象的3倍少20年。
海象的寿命大约是多少?
海象寿命×3-20=蓝鲸寿命
解:设海象的寿命大约是x年。
3x-20=100
3x-20+20=100+20
3x=120
3x÷3=120÷3
x
=
40
方程左边=3x-20
=3╳40-20
=120-20
=100
=方程右边
所以:x=
40是所列方程的解。
检验:
答:海象的寿命大约是40年。
3、先说说下列各题的数量关系,再列方程解决问题。
天安门广场的面积╳2-16=故宫的面积(72万m?)
解:设天安门广场的面积是x万平方米。
2x-16=72
2x-16+16=72+16
2
x
=
88
2x÷2=88÷2
x
=
44
方程左边=2x-16
=2╳44-16
=88-16
=722
=方程右边
所以:x=
44是所列方程的解。
检验:
答:天安门广场的面积是44万平方米。
故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。天安门广场的面积是多少万平方米?
用方程解答。
2.
一头大象的体重是4吨,比一头牛体重的4倍还多0.2吨。这头牛体重多少吨?
3.
四、总结质疑
反思评价
1.
今天这节课你有哪些收获?
2.这节课你学会了用什么方法来解决实际问题?
3.什么类型的题目适合用今天所学的方法来解答?
4.用这样的方法来解决实际问题时要注意什么?
作业
四、总结质疑
反思评价
1.
回顾一下,今天这节课你有哪些收获?
(1)已知标准量,求比较量,用算式方法解比较简单;逆向思维的问题
用方程解能使它变成顺向,降低难度,用方程解比较简单。
(2)把没有学过的方程转化成学过的方程,数学中很多地方都要用到这种方法,
化繁为简,化难为易,化新知为旧知。
(3)对于复杂的问题,我们可以画线段图,分析数量关系,理解题意。
(4)列方程解决问题要记住步骤,书写要规范,并自觉养成检验的习惯。
