高中数学人教A版(2019)必修第一册第四章4.4《对数函数及其性质》 教 案(word版)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册第四章4.4《对数函数及其性质》 教 案(word版) |

|
|
| 格式 | docx | ||
| 文件大小 | 260.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 17:24:23 | ||
图片预览


文档简介
《对数函数及其性质》
教材分析
本节内容是在学习了指数函数后,通过具体实例了解对数函数模型的实际背景,学习对数的概念进而学习对数函数.教材的编写中反映了指数函数与对数函数的很多对应关系,为反函数的提出作为铺垫.本本节的重难点是对数函数的定义、图像和性质.解决有关对数函数的问题时,一要注意对数函数的定义域,二要注意底数的取值范围的限制,需要分类讨论时一定要分类讨论.
教学目标
1.对数函数的概念,熟悉对数函数的图像与性质规律. 掌握对数函数的性质,能初步运用性质解决问题.
2.让学生通过观察对数函数的图像,发现并归纳对数函数的性质. 学生通过观察和类比函数图像,体会两种函数的单调性差异.
3.培养学生数形结合的思想以及分析推理的能力,体会指数函数与对数函数互为反函数,培养学生严谨的科学态度.
教学重难点
【教学重点】
理解对数函数的定义,掌握对数函数的图像和性质. 理解指数函数与对数函数内在联系.
【教学难点】
底数a对图像的影响及对数函数性质的作用.
课前准备
回顾指数与指数函数的性质和对数与对数的运算,阅读材料《对数的发明》.
教学过程
1.设置情境
在2.2.1的例6中,考古学家利用估算出土文物或古遗址的年代,对于每一个C14含量P,通过关系式,都有唯一确定的年代与之对应.同理,对于每一个对数式中的,任取一个正的实数值,均有唯一的值与之对应,所以的函数.
2.探索新知
一般地,我们把函数(>0且≠1)叫做对数函数,其中是自变量,函数的定义域是(0,+∞).
提问:(1)在函数的定义中,为什么要限定>0且≠1.
(2)为什么对数函数(>0且≠1)的定义域是(0,+∞).组织学生充分讨论、交流,使学生更加理解对数函数的含义,从而加深对对数函数的理解.
答:①根据对数与指数式的关系,知可化为,由指数的概念,要使有意义,必须规定>0且≠1.
②因为可化为,不管取什么值,由指数函数的性质,>0,所以.
下面我们来研究函数的图像,并通过图像来研究函数的性质:
先完成P81表2-3,并根据此表用描点法或用电脑画出函数 再利用电脑软件画出
1
2
4
6
8
12
16
-1
0
1
2
2.58
3
3.58
4
y
0 x
注意到:,若点的图像上,则点的图像上. 由于()与()关于轴对称,因此,的图像与的图像关于轴对称. 所以,由此我们可以画出的图像.
先由学生自己画出的图像,再由电脑软件画出与的图像.
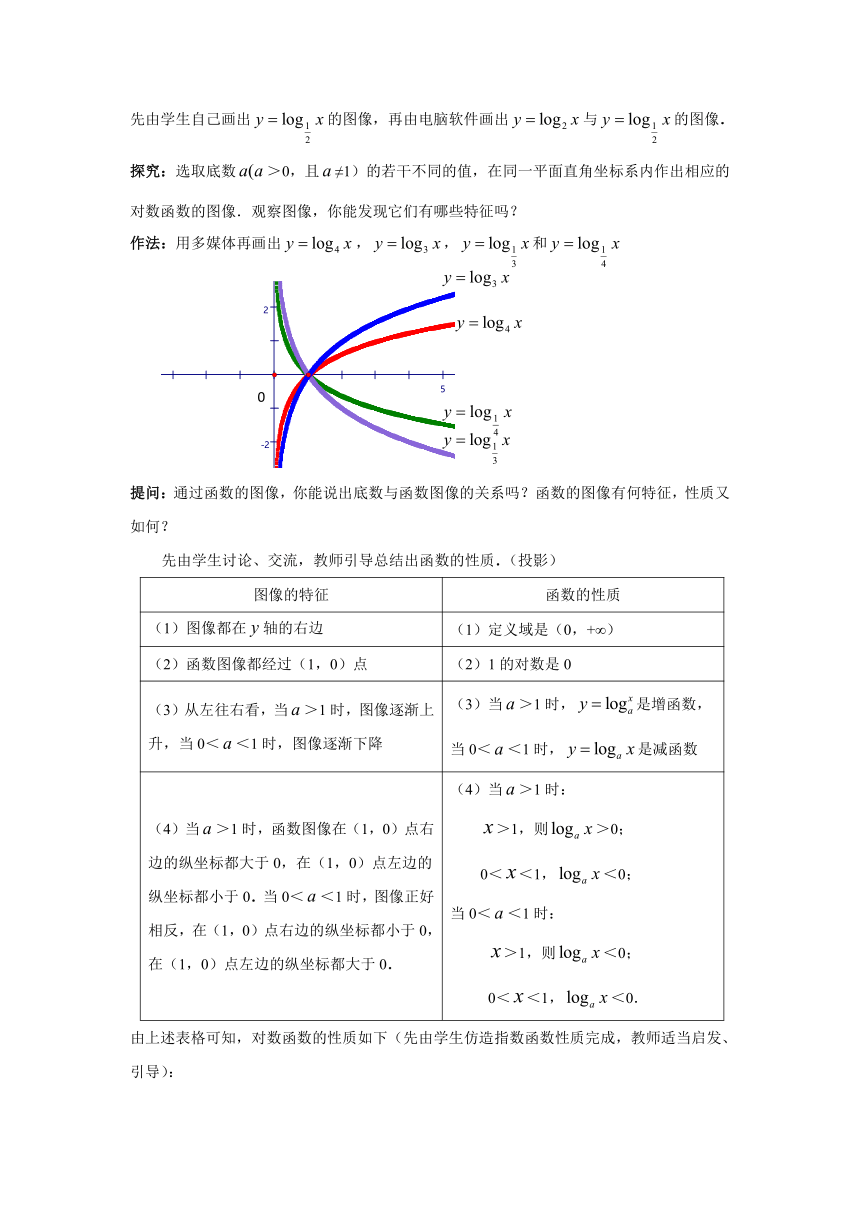
探究:选取底数>0,且≠1)的若干不同的值,在同一平面直角坐标系内作出相应的对数函数的图像.观察图像,你能发现它们有哪些特征吗?
作法:用多媒体再画出,,和
0
提问:通过函数的图像,你能说出底数与函数图像的关系吗?函数的图像有何特征,性质又如何?
先由学生讨论、交流,教师引导总结出函数的性质.(投影)
图像的特征
函数的性质
(1)图像都在轴的右边
(1)定义域是(0,+∞)
(2)函数图像都经过(1,0)点
(2)1的对数是0
(3)从左往右看,当>1时,图像逐渐上升,当0<<1时,图像逐渐下降
(3)当>1时,是增函数,当0<<1时,是减函数
(4)当>1时,函数图像在(1,0)点右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0.当0<<1时,图像正好相反,在(1,0)点右边的纵坐标都小于0,在(1,0)点左边的纵坐标都大于0.
(4)当>1时:
>1,则>0;
0<<1,<0;
当0<<1时:
>1,则<0;
0<<1,<0.
由上述表格可知,对数函数的性质如下(先由学生仿造指数函数性质完成,教师适当启发、引导):
>1
0<<1
图
像
49784086995
58420087630
性
质
(1)定义域(0,+∞);
(2)值域R;
(3)过点(1,0),即当=1,=0;
(4)在(0,+∞)上是增函数
在(0,+∞)是上减函数
3.例题讲解
例1 求下列函数的定义域
(1) (2) (>0且≠1)
分析:由对数函数的定义知:>0;>0,解出不等式就可求出定义域.
解:(1)因为>0,即≠0,所以函数的定义域为.
(2)因为>0,即<4,所以函数的定义域为<.
例2 比较下列各组数中的两个值大小
(1)
(2)
(3) (>0,且≠1)
分析:由数形结合的方法或利用函数的单调性来完成:
(1)解法1:用图形计算器或多媒体画出对数函数的图像.在图像上,横坐标为3、4的点在横坐标为8.5的点的下方:
所以,
解法2:由函数+上是单调增函数,且3.4<8.5,所以.
解法3:直接用计算器计算得:,
(2)第(2)小题类似
(3)注:底数是常数,但要分类讨论的范围,再由函数单调性判断大小.
解法1:当>1时,在(0,+∞)上是增函数,且5.1<5.9.
所以,
当1时,在(0,+∞)上是减函数,且5.1<5.9.
所以,
解法2:转化为指数函数,再由指数函数的单调判断大小不一,
令 令 则
当>1时,在R上是增函数,且5.1<5.9
所以,<,即<
当0<<1时,在R上是减函数,且5.1>5.9
所以,<,即>
说明:先画图像,由数形结合方法解答
4.课堂练习:
教材对应习题.
5.反函数
探究:在指数函数中,为自变量,为因变量,如果把当成自变量,当成因变量,那么是的函数吗?如果是,那么对应关系是什么?如果不是,请说明理由.
引导学生通过观察、类比、思考与交流,得出结论.
在指数函数中,是自变量, 是的函数(),而且其在R上是单调递增函数.过轴正半轴上任意一点作轴的平行线,与的图像有且只有一个交点.由指数式与对数式关系,,即对于每一个,在关系式的作用之下,都有唯一的确定的值和它对应,所以,可以把作为自变量,作为的函数,我们说.
从我们的列表中知道,是同一个函数图像.
引出反函数的概念(只让学生理解,加宽学生视野)
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数为反函数.
由反函数的概念可知,同底的指数函数和对数函数互为反函数.
如的反函数,但习惯上,通常以表示自变量,表示函数,对调中的,这样是指数函的反函数.
以后,我们所说的反函数是对调后的函数,如的反函数是.
同理,>1)的反函数是>0且.
课堂练习:求下列函数的反函数
(1) (2)
补充练习
1.已知函数的定义域为[-1,1],则函数的定义域为 .
2.求函数的值域.
3.已知<<0,按大小顺序排列m, n, 0, 1.
4.已知0<<1, b>1, ab>1. 比较.
6.归纳小结:
(1)对数函数的概念必要性与重要性;
(2)对数函数的性质,列表展现.
(3)反函数.
7.布置作业
教材对应习题.
教学反思
略.
教材分析
本节内容是在学习了指数函数后,通过具体实例了解对数函数模型的实际背景,学习对数的概念进而学习对数函数.教材的编写中反映了指数函数与对数函数的很多对应关系,为反函数的提出作为铺垫.本本节的重难点是对数函数的定义、图像和性质.解决有关对数函数的问题时,一要注意对数函数的定义域,二要注意底数的取值范围的限制,需要分类讨论时一定要分类讨论.
教学目标
1.对数函数的概念,熟悉对数函数的图像与性质规律. 掌握对数函数的性质,能初步运用性质解决问题.
2.让学生通过观察对数函数的图像,发现并归纳对数函数的性质. 学生通过观察和类比函数图像,体会两种函数的单调性差异.
3.培养学生数形结合的思想以及分析推理的能力,体会指数函数与对数函数互为反函数,培养学生严谨的科学态度.
教学重难点
【教学重点】
理解对数函数的定义,掌握对数函数的图像和性质. 理解指数函数与对数函数内在联系.
【教学难点】
底数a对图像的影响及对数函数性质的作用.
课前准备
回顾指数与指数函数的性质和对数与对数的运算,阅读材料《对数的发明》.
教学过程
1.设置情境
在2.2.1的例6中,考古学家利用估算出土文物或古遗址的年代,对于每一个C14含量P,通过关系式,都有唯一确定的年代与之对应.同理,对于每一个对数式中的,任取一个正的实数值,均有唯一的值与之对应,所以的函数.
2.探索新知
一般地,我们把函数(>0且≠1)叫做对数函数,其中是自变量,函数的定义域是(0,+∞).
提问:(1)在函数的定义中,为什么要限定>0且≠1.
(2)为什么对数函数(>0且≠1)的定义域是(0,+∞).组织学生充分讨论、交流,使学生更加理解对数函数的含义,从而加深对对数函数的理解.
答:①根据对数与指数式的关系,知可化为,由指数的概念,要使有意义,必须规定>0且≠1.
②因为可化为,不管取什么值,由指数函数的性质,>0,所以.
下面我们来研究函数的图像,并通过图像来研究函数的性质:
先完成P81表2-3,并根据此表用描点法或用电脑画出函数 再利用电脑软件画出
1
2
4
6
8
12
16
-1
0
1
2
2.58
3
3.58
4
y
0 x
注意到:,若点的图像上,则点的图像上. 由于()与()关于轴对称,因此,的图像与的图像关于轴对称. 所以,由此我们可以画出的图像.
先由学生自己画出的图像,再由电脑软件画出与的图像.
探究:选取底数>0,且≠1)的若干不同的值,在同一平面直角坐标系内作出相应的对数函数的图像.观察图像,你能发现它们有哪些特征吗?
作法:用多媒体再画出,,和
0
提问:通过函数的图像,你能说出底数与函数图像的关系吗?函数的图像有何特征,性质又如何?
先由学生讨论、交流,教师引导总结出函数的性质.(投影)
图像的特征
函数的性质
(1)图像都在轴的右边
(1)定义域是(0,+∞)
(2)函数图像都经过(1,0)点
(2)1的对数是0
(3)从左往右看,当>1时,图像逐渐上升,当0<<1时,图像逐渐下降
(3)当>1时,是增函数,当0<<1时,是减函数
(4)当>1时,函数图像在(1,0)点右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0.当0<<1时,图像正好相反,在(1,0)点右边的纵坐标都小于0,在(1,0)点左边的纵坐标都大于0.
(4)当>1时:
>1,则>0;
0<<1,<0;
当0<<1时:
>1,则<0;
0<<1,<0.
由上述表格可知,对数函数的性质如下(先由学生仿造指数函数性质完成,教师适当启发、引导):
>1
0<<1
图
像
49784086995
58420087630
性
质
(1)定义域(0,+∞);
(2)值域R;
(3)过点(1,0),即当=1,=0;
(4)在(0,+∞)上是增函数
在(0,+∞)是上减函数
3.例题讲解
例1 求下列函数的定义域
(1) (2) (>0且≠1)
分析:由对数函数的定义知:>0;>0,解出不等式就可求出定义域.
解:(1)因为>0,即≠0,所以函数的定义域为.
(2)因为>0,即<4,所以函数的定义域为<.
例2 比较下列各组数中的两个值大小
(1)
(2)
(3) (>0,且≠1)
分析:由数形结合的方法或利用函数的单调性来完成:
(1)解法1:用图形计算器或多媒体画出对数函数的图像.在图像上,横坐标为3、4的点在横坐标为8.5的点的下方:
所以,
解法2:由函数+上是单调增函数,且3.4<8.5,所以.
解法3:直接用计算器计算得:,
(2)第(2)小题类似
(3)注:底数是常数,但要分类讨论的范围,再由函数单调性判断大小.
解法1:当>1时,在(0,+∞)上是增函数,且5.1<5.9.
所以,
当1时,在(0,+∞)上是减函数,且5.1<5.9.
所以,
解法2:转化为指数函数,再由指数函数的单调判断大小不一,
令 令 则
当>1时,在R上是增函数,且5.1<5.9
所以,<,即<
当0<<1时,在R上是减函数,且5.1>5.9
所以,<,即>
说明:先画图像,由数形结合方法解答
4.课堂练习:
教材对应习题.
5.反函数
探究:在指数函数中,为自变量,为因变量,如果把当成自变量,当成因变量,那么是的函数吗?如果是,那么对应关系是什么?如果不是,请说明理由.
引导学生通过观察、类比、思考与交流,得出结论.
在指数函数中,是自变量, 是的函数(),而且其在R上是单调递增函数.过轴正半轴上任意一点作轴的平行线,与的图像有且只有一个交点.由指数式与对数式关系,,即对于每一个,在关系式的作用之下,都有唯一的确定的值和它对应,所以,可以把作为自变量,作为的函数,我们说.
从我们的列表中知道,是同一个函数图像.
引出反函数的概念(只让学生理解,加宽学生视野)
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数为反函数.
由反函数的概念可知,同底的指数函数和对数函数互为反函数.
如的反函数,但习惯上,通常以表示自变量,表示函数,对调中的,这样是指数函的反函数.
以后,我们所说的反函数是对调后的函数,如的反函数是.
同理,>1)的反函数是>0且.
课堂练习:求下列函数的反函数
(1) (2)
补充练习
1.已知函数的定义域为[-1,1],则函数的定义域为 .
2.求函数的值域.
3.已知<<0,按大小顺序排列m, n, 0, 1.
4.已知0<<1, b>1, ab>1. 比较.
6.归纳小结:
(1)对数函数的概念必要性与重要性;
(2)对数函数的性质,列表展现.
(3)反函数.
7.布置作业
教材对应习题.
教学反思
略.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
