北师大版七年级数学上册第四章 基本平面图形综合测评(Word版 含答案)
文档属性
| 名称 | 北师大版七年级数学上册第四章 基本平面图形综合测评(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 322.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 13:20:00 | ||
图片预览

文档简介
第四章? 基本平面图形综合测评
(本试卷满分100分)??
一、选择题(本大题共10小题,每小题3分,共30分)
1. 如图1,下列说法中正确的是( )
A. ∠BAC和∠DAE不是同一个角 B. ∠ADE可以用∠D表示
C. ∠ABC可以用∠B表示 D. ∠ABC和∠ACB是同一个角
图1
2. 木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点,有无数条直线 D. 连接两点之间的线段叫做两点间的距离
3. 将一副直角三角尺按下列不同方式摆放,图中∠α与∠β相等的是( )
A B C D
4. 如图2,已知点 A,B,C 是同一条直线上的三个点,若图中共有a条线段,b条射线,则a+b的值为( )
A. 6 B. 7 C. 8 D. 9
图2 图3 图4
5. 如图3,已知∠AOD=84°,∠AOB=18°,若OB平分∠AOC,则∠COD的度数是( )
A. 66° B. 48° C. 42° D. 36°
6.若∠A=40°18′,∠B=40°15″,∠C=40.25°,则有( )
A.∠A>∠B>∠C B.∠B>∠A>∠C C.∠A>∠C>∠B D.∠C>∠A>∠B
7. 如图4,点C,D在线段AB上,则下列表述或结论错误的是( )
A. 若AC=BD,则AD=BC B. AC=AD+DB-BC
C. AD=AB+CD-BC D. 图中共有线段12条
8.下列说法正确的是( )
A.若AC=BC,则点C是线段AB的中点
B.30.15°=30°15'
C.若经过某个多边形一个顶点的所有对角线,将这个多边形分成七个三角形,则这个多边形是八边形
D.钟表上的时间是11点10分,此时时针与分针所成的夹角是85°
9.(2020年凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12 cm,则线段BD的长为( )
A.10 cm B.8 cm C.10 cm?或8 cm D.2 cm?或4 cm
10.如图5,已知∠AOB=90°,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,有下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC+∠BOD=90°.其中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
图5
二、填空题(本大题共6小题,每小题3分,共18分)
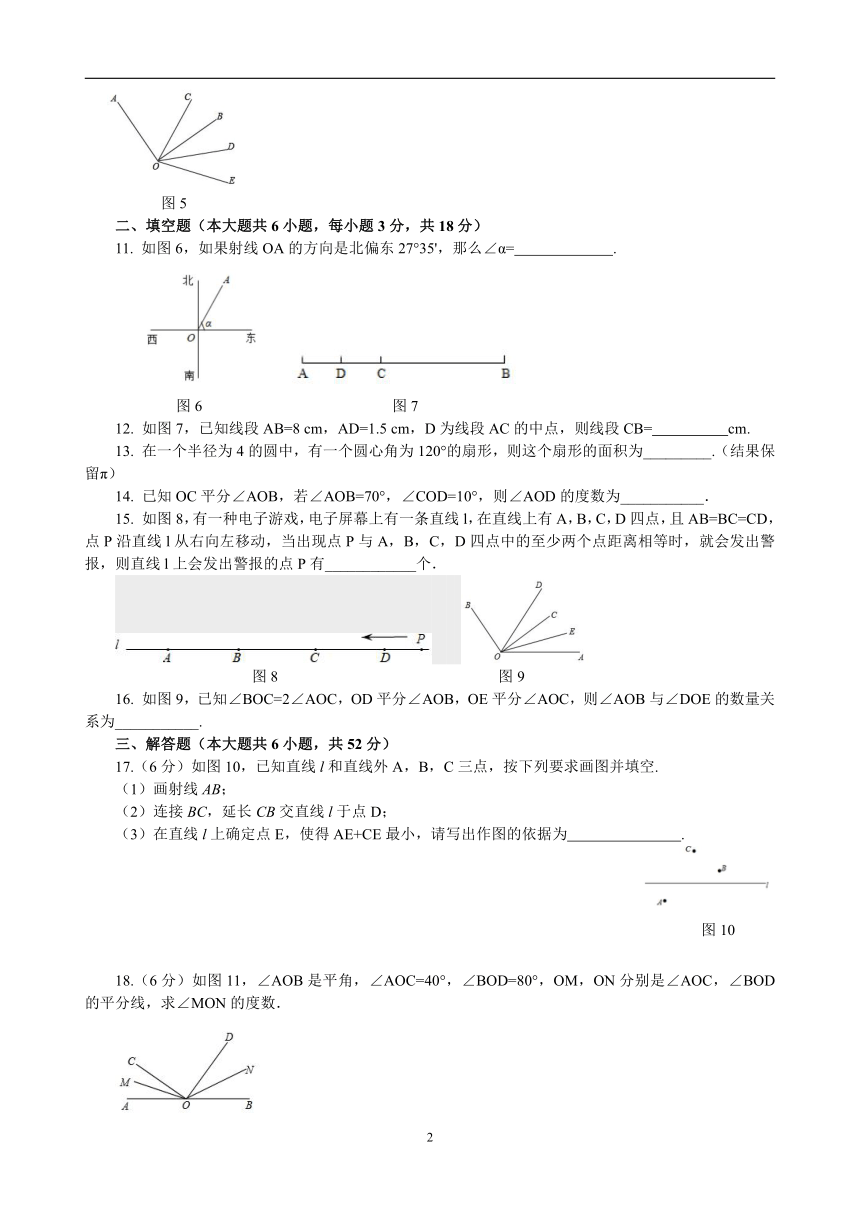
11. 如图6,如果射线OA的方向是北偏东27°35',那么∠α= .
图6 图7
12. 如图7,已知线段AB=8 cm,AD=1.5 cm,D为线段AC的中点,则线段CB= 5cm.
在一个半径为4的圆中,有一个圆心角为120°的扇形,则这个扇形的面积为_________.(结果保留π)
已知OC平分∠AOB,若∠AOB=70°,∠COD=10°,则∠AOD的度数为___________.
15. 如图8,有一种电子游戏,电子屏幕上有一条直线l,在直线上有A,B,C,D四点,且AB=BC=CD,点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P有____________个.
图8 图9
16. 如图9,已知∠BOC=2∠AOC,OD平分∠AOB,OE平分∠AOC,则∠AOB与∠DOE的数量关系为___________.
三、解答题(本大题共6小题,共52分)
17.(6分)如图10,已知直线l和直线外A,B,C三点,按下列要求画图并填空.
(1)画射线AB;
(2)连接BC,延长CB交直线l于点D;
(3)在直线l上确定点E,使得AE+CE最小,请写出作图的依据为 .
图10
18.(6分)如图11,∠AOB是平角,∠AOC=40°,∠BOD=80°,OM,ON分别是∠AOC,∠BOD的平分线,求∠MON的度数.
图11
19.(8分)如图12,已知点A为线段CB上的一点.
(1)根据要求画出图形(尺规作图,不要求写法,保留作图痕迹):延长AB至点D,使BD=AB;反向延长CA至点E,使CE=CA;
(2)如果ED=18,BD=6,求CA的长.
图12
20.(10分)如图13,一、二、三、四这四个扇形的面积之比为1:3:5:1.
(1)请分别求出它们圆心角的度数.
(2)一、二、四这三个扇形的圆心角的度数之和是多少?
图13
21.(10分)如图14,已知∠AOC:∠BOC=3:4,∠COD=∠AOD,OE平分∠BOC,且∠DOE=60°.
(1)图中共有__________个角;
(2)求∠AOE的度数.
图14
22.(12分)如图15,点C在线段AB上,M,N分别是线段AC,BC的中点.
(1)若AC=7 cm,BC=5 cm,求线段MN的长;
(2)若AB=a,C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;
(3)若将(2)中“C为线段AB上任意一点”改为“C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.
图15
附加题(20分,不计入总分)
如图所示,以直线AB上一点O为端点作射线OC,使∠BOC=60°,将一块直角三角尺DOE的直角顶点放在O处,一边OD放在射线OB上,将直角三角尺DOE绕点O逆时针方向旋转至OE边第一次与射线OA重合时停止.
(1)如图①,边OD在射线OB上,则∠COE = ;
(2)如图②,若OE恰好平分∠AOC,则∠BOD = ;
(3)如图③,若∠COE=105°,求∠BOD的度数;
(4)在旋转过程中,请写出∠COE与∠BOD始终保持的数量关系,并请说明理由.
② ③
第四章? 基本平面图形综合测评
一、1. C 2. B 3. C 4. D 5. B 6. C 7. D 8. D 9. C 10. A
二、11. 62°25′ 12. 5 13. 14. 25°或45° 15. 5 16. ∠AOB=3∠DOE
三、17. 解:(1)如图1所示,射线AB即为所求;
(2)如图1所示,线段CB,射线CD即为所求;
(3)如图1所示,点E即为所求.依据为:两点之间,线段最短.
图1
18. 解:因为∠AOC+∠COD+∠BOD=∠AOB,∠AOB是平角,∠AOC=40°,∠BOD=80°,所以∠COD=180°-
∠AOC-∠BOD=180°-40°-80°=60°.因为OM,ON分别是∠AOC,∠BOD的平分线,所以∠COM=∠AOC=20°,∠NOD=∠BOD=40°.所以∠MON=∠COM+∠COD+∠DON=20°+60°
+40°=120°.
19. 解:(1)画出的图形如图2所示.
图2
(2)因为BD=AB,BD=6,所以AB=6.因为ED=18,所以AE=ED-AB-BD=18-6-6=6.因为CE=CA,所以AC=AE= ×6=3.
20. 解:(1)因为一、二、三、四这四个扇形的面积之比为1:3:5:1,所以各个扇形的面积分别占整个圆面积的,,,.所以各个扇形的圆心角的度数分别为×360°=36°,×360°=108°,×360°=180°,×360°=36°.
(2)一、二、四这三个扇形的圆心角的度数之和是36°+36°+108°=180°.
21. 解:(1)10
(2)设∠AOC=3x,则∠BOC=4x.因为∠COD=∠AOD,所以∠COD=∠AOC=x.因为OE平分∠BOC,所以∠COE=∠BOC=2x.所以∠DOE=∠COD+∠COE=x+2x=60°,解得x=20°.
所以∠AOE=∠AOC+∠COE=5x=100°.
22.解:(1)因为AC=7 cm,M是线段AC的中点,所以MC=AC=cm.因为BC=5 cm,N是线段BC的中点,所以CN=BC=cm.所以MN=MC+CN=6 cm.
(2)能.因为M是线段AC的中点,所以MC=AC.因为N是线段BC的中点,所以CN=BC.所以MN=MC+CN=AC+BC=AB=a.
(3)结论成立.理由如下:当点C在线段AB的延长线上时,如图3.因为N为BC的中点,所以CN=BN=BC.
因为M是AC的中点,所以MC=AC.所以MN=MC-NC=AC-BC=AB.
当点C在线段BA的延长线上时,如图4.因为N是线段BC的中点,所以CN=BN=BC.因为M是线段AC的中点,所以MC=AC.所以MN=NC-CM=BC-AC=AB.
综上所述,(2)的结论成立.
附加题:解:(1)30 (2)30
因为∠COE=105°,所以∠COD=∠COE-∠DOE=105°-90°=15°.所以∠BOD=∠COD+∠BOC=15°+60°=75.
(4)∠COE-∠BOD=30°.理由如下:①当OD在∠BOC的内部时,如图1.因为∠COE+∠COD=∠DOE=90°,所以∠COE+(∠BOC-∠BOD)=90°,即∠COE+60°-∠BOD=90°,所以∠COE-∠BOD=30°.
图1 图2
②当OD在∠BOC的外部时,如图2.因为∠COE-∠COD=∠DOE=90°,所以∠COE-(∠BOD-∠BOC)=90°,即∠COE-∠BOD+60°=90°.所以∠COE-∠BOD=30°.
综上,∠COE-∠BOD=30°.
(本试卷满分100分)??
一、选择题(本大题共10小题,每小题3分,共30分)
1. 如图1,下列说法中正确的是( )
A. ∠BAC和∠DAE不是同一个角 B. ∠ADE可以用∠D表示
C. ∠ABC可以用∠B表示 D. ∠ABC和∠ACB是同一个角
图1
2. 木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点,有无数条直线 D. 连接两点之间的线段叫做两点间的距离
3. 将一副直角三角尺按下列不同方式摆放,图中∠α与∠β相等的是( )
A B C D
4. 如图2,已知点 A,B,C 是同一条直线上的三个点,若图中共有a条线段,b条射线,则a+b的值为( )
A. 6 B. 7 C. 8 D. 9
图2 图3 图4
5. 如图3,已知∠AOD=84°,∠AOB=18°,若OB平分∠AOC,则∠COD的度数是( )
A. 66° B. 48° C. 42° D. 36°
6.若∠A=40°18′,∠B=40°15″,∠C=40.25°,则有( )
A.∠A>∠B>∠C B.∠B>∠A>∠C C.∠A>∠C>∠B D.∠C>∠A>∠B
7. 如图4,点C,D在线段AB上,则下列表述或结论错误的是( )
A. 若AC=BD,则AD=BC B. AC=AD+DB-BC
C. AD=AB+CD-BC D. 图中共有线段12条
8.下列说法正确的是( )
A.若AC=BC,则点C是线段AB的中点
B.30.15°=30°15'
C.若经过某个多边形一个顶点的所有对角线,将这个多边形分成七个三角形,则这个多边形是八边形
D.钟表上的时间是11点10分,此时时针与分针所成的夹角是85°
9.(2020年凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12 cm,则线段BD的长为( )
A.10 cm B.8 cm C.10 cm?或8 cm D.2 cm?或4 cm
10.如图5,已知∠AOB=90°,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,有下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC+∠BOD=90°.其中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
图5
二、填空题(本大题共6小题,每小题3分,共18分)
11. 如图6,如果射线OA的方向是北偏东27°35',那么∠α= .
图6 图7
12. 如图7,已知线段AB=8 cm,AD=1.5 cm,D为线段AC的中点,则线段CB= 5cm.
在一个半径为4的圆中,有一个圆心角为120°的扇形,则这个扇形的面积为_________.(结果保留π)
已知OC平分∠AOB,若∠AOB=70°,∠COD=10°,则∠AOD的度数为___________.
15. 如图8,有一种电子游戏,电子屏幕上有一条直线l,在直线上有A,B,C,D四点,且AB=BC=CD,点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P有____________个.
图8 图9
16. 如图9,已知∠BOC=2∠AOC,OD平分∠AOB,OE平分∠AOC,则∠AOB与∠DOE的数量关系为___________.
三、解答题(本大题共6小题,共52分)
17.(6分)如图10,已知直线l和直线外A,B,C三点,按下列要求画图并填空.
(1)画射线AB;
(2)连接BC,延长CB交直线l于点D;
(3)在直线l上确定点E,使得AE+CE最小,请写出作图的依据为 .
图10
18.(6分)如图11,∠AOB是平角,∠AOC=40°,∠BOD=80°,OM,ON分别是∠AOC,∠BOD的平分线,求∠MON的度数.
图11
19.(8分)如图12,已知点A为线段CB上的一点.
(1)根据要求画出图形(尺规作图,不要求写法,保留作图痕迹):延长AB至点D,使BD=AB;反向延长CA至点E,使CE=CA;
(2)如果ED=18,BD=6,求CA的长.
图12
20.(10分)如图13,一、二、三、四这四个扇形的面积之比为1:3:5:1.
(1)请分别求出它们圆心角的度数.
(2)一、二、四这三个扇形的圆心角的度数之和是多少?
图13
21.(10分)如图14,已知∠AOC:∠BOC=3:4,∠COD=∠AOD,OE平分∠BOC,且∠DOE=60°.
(1)图中共有__________个角;
(2)求∠AOE的度数.
图14
22.(12分)如图15,点C在线段AB上,M,N分别是线段AC,BC的中点.
(1)若AC=7 cm,BC=5 cm,求线段MN的长;
(2)若AB=a,C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;
(3)若将(2)中“C为线段AB上任意一点”改为“C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.
图15
附加题(20分,不计入总分)
如图所示,以直线AB上一点O为端点作射线OC,使∠BOC=60°,将一块直角三角尺DOE的直角顶点放在O处,一边OD放在射线OB上,将直角三角尺DOE绕点O逆时针方向旋转至OE边第一次与射线OA重合时停止.
(1)如图①,边OD在射线OB上,则∠COE = ;
(2)如图②,若OE恰好平分∠AOC,则∠BOD = ;
(3)如图③,若∠COE=105°,求∠BOD的度数;
(4)在旋转过程中,请写出∠COE与∠BOD始终保持的数量关系,并请说明理由.
② ③
第四章? 基本平面图形综合测评
一、1. C 2. B 3. C 4. D 5. B 6. C 7. D 8. D 9. C 10. A
二、11. 62°25′ 12. 5 13. 14. 25°或45° 15. 5 16. ∠AOB=3∠DOE
三、17. 解:(1)如图1所示,射线AB即为所求;
(2)如图1所示,线段CB,射线CD即为所求;
(3)如图1所示,点E即为所求.依据为:两点之间,线段最短.
图1
18. 解:因为∠AOC+∠COD+∠BOD=∠AOB,∠AOB是平角,∠AOC=40°,∠BOD=80°,所以∠COD=180°-
∠AOC-∠BOD=180°-40°-80°=60°.因为OM,ON分别是∠AOC,∠BOD的平分线,所以∠COM=∠AOC=20°,∠NOD=∠BOD=40°.所以∠MON=∠COM+∠COD+∠DON=20°+60°
+40°=120°.
19. 解:(1)画出的图形如图2所示.
图2
(2)因为BD=AB,BD=6,所以AB=6.因为ED=18,所以AE=ED-AB-BD=18-6-6=6.因为CE=CA,所以AC=AE= ×6=3.
20. 解:(1)因为一、二、三、四这四个扇形的面积之比为1:3:5:1,所以各个扇形的面积分别占整个圆面积的,,,.所以各个扇形的圆心角的度数分别为×360°=36°,×360°=108°,×360°=180°,×360°=36°.
(2)一、二、四这三个扇形的圆心角的度数之和是36°+36°+108°=180°.
21. 解:(1)10
(2)设∠AOC=3x,则∠BOC=4x.因为∠COD=∠AOD,所以∠COD=∠AOC=x.因为OE平分∠BOC,所以∠COE=∠BOC=2x.所以∠DOE=∠COD+∠COE=x+2x=60°,解得x=20°.
所以∠AOE=∠AOC+∠COE=5x=100°.
22.解:(1)因为AC=7 cm,M是线段AC的中点,所以MC=AC=cm.因为BC=5 cm,N是线段BC的中点,所以CN=BC=cm.所以MN=MC+CN=6 cm.
(2)能.因为M是线段AC的中点,所以MC=AC.因为N是线段BC的中点,所以CN=BC.所以MN=MC+CN=AC+BC=AB=a.
(3)结论成立.理由如下:当点C在线段AB的延长线上时,如图3.因为N为BC的中点,所以CN=BN=BC.
因为M是AC的中点,所以MC=AC.所以MN=MC-NC=AC-BC=AB.
当点C在线段BA的延长线上时,如图4.因为N是线段BC的中点,所以CN=BN=BC.因为M是线段AC的中点,所以MC=AC.所以MN=NC-CM=BC-AC=AB.
综上所述,(2)的结论成立.
附加题:解:(1)30 (2)30
因为∠COE=105°,所以∠COD=∠COE-∠DOE=105°-90°=15°.所以∠BOD=∠COD+∠BOC=15°+60°=75.
(4)∠COE-∠BOD=30°.理由如下:①当OD在∠BOC的内部时,如图1.因为∠COE+∠COD=∠DOE=90°,所以∠COE+(∠BOC-∠BOD)=90°,即∠COE+60°-∠BOD=90°,所以∠COE-∠BOD=30°.
图1 图2
②当OD在∠BOC的外部时,如图2.因为∠COE-∠COD=∠DOE=90°,所以∠COE-(∠BOD-∠BOC)=90°,即∠COE-∠BOD+60°=90°.所以∠COE-∠BOD=30°.
综上,∠COE-∠BOD=30°.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
