2.6.3 有理数的加减混合运算教学课件(共21张PPT)
文档属性
| 名称 | 2.6.3 有理数的加减混合运算教学课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 15:45:21 | ||
图片预览








文档简介
(共21张PPT)
北师大版
初中数学
北师大版七年级数学(上册)
第二章
有理数及其运算
2.6有理数的加减混合运算
第三课时
学习目标
1.熟悉在水位变化过程中出现的量,进一步加深对有理数意义的理解,巩固有理数在实际生活中的作用.
2.能综合运用有理数及其加减法的有关知识,解决简单的实际问题,体会数学与现实生活的联系.
温故而知新
2.减法可以转化为加法,再写成代数和的形式,
如(-12)+(-5)-(-7)-(+6)=
.
1.加法分为
和
相加,关键在于确定
.
正
负
-12-5+7-6
确定符号
某电动自行车制造厂计划前半年内每月生产汽车360辆,由于另有任务,每月上班人数有变化,1月至6月实际每月生产量和计划每月生产量相比,变化情况如下(增加为正,减少为负,单位:辆):
+5,-3,-2,+7,+1,-6.
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
解:(1)(+7)-(-6)=13(辆).
故生产量最多的一个月比生产量最少的一个月多生产了13辆;
导入新课
(2)前半年的实际总产量是多少?比计划的总产量多了还是少了?相差多少?
解:(2)前半年实际总产量为
(+5)+(-3)+(-2)+(+7)+(+1)+(-6)
=+2(辆).
所以比原计划的总产量多了2辆.
右图是流花河的水文资料(单位:m)如果取河流的警戒水位
为0点,那么图中的其它数据可以记作什么?
解:最高水位可以记作:35.3-33.4=+1.9(m).
平均水位可以记作:22.6-33.4=-10.8(m).
最低水位可以记作:11.5-33.4=-21.9(m).
探究新知
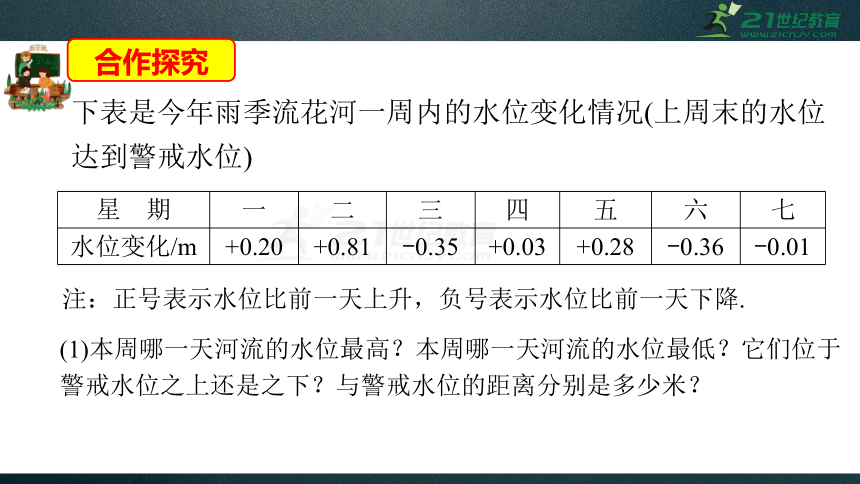
下表是今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位)
星
期
一
二
三
四
五
六
七
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?本周哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
合作探究
(1)本周哪一天河流的水位最高?本周哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
解:本周每天水位记录为:
周一:33.4+0.20=33.6(m)
周二:33.4+0.20+0.81=34.41(m)
周三:33.4+0.20+0.81-0.35=34.06(m)
周四:33.4+0.20+0.81-0.35+0.03=34.09(m)
周五:33.4+0.20+0.81-0.35+0.03+0.28=34.37(m)
周六:33.4+0.20+0.81-0.35+0.03+0.28-0.36=34.01(m)
周日:33.4+0.20+0.81-0.35+0.03+0.28-0.36-0.01=34.00(m)
所以周二的水位最高,周一的水位最低;
它们都在警戒水位以上,
其中,最高水位与警戒水位的距离是34.41-33.4=1.01(m)
或0.20+0.81=1.01(m),
最低水位与警戒水位的距离是33.6-33.4=0.2(m).
(2)与上周末相比,本周末河流水位是上升了还是下降了?
解:上周末的水位记录为33.4m,
本周末的水位记录为34.00m,
与周末相比,本周末的水位是上升了.
(3)完成下面的本周水位记录表:
星
期
一
二
三
四
五
六
七
水位记录/m
33.6
34.00
33.41
34.06
34.09
34.37
34.01
(4)以警戒水位为0点,用折线统计图表示本周的水位情况.
某校八年级1班的所有男同学进行了100米跑步测试,达标成绩为15s,下表是某小组7名男生的成绩记录(单位:s)
注:正数表示成绩大于15s,负数表示成绩小于15s.
(1)这七名同学中编号为多少的成绩最高?成绩是多少s?
解:(1)编号为3的同学的成绩最高,
15-1.2=13.8(s);
例题解析
编号
1
2
3
4
5
6
7
8
成绩(s)
-0.8
+1
-1.2
0
-0.7
+0.6
-0.4
-0.1
(2)这个小组男生的达标率是多少?
解:(2)根据题意,可知成绩即为正数的不达标,故有2人不达标,6人达标,
所以这个小组男生的达标率是6÷8×100%=75%.
(3)这个小组男生的平均成绩是多少?
(-0.8)+(+1)+(-1.2)+(0)+(-0.7)+(+0.6)+(-0.4)+(-0.1)=-1.6(s)
15-1.6÷8=14.8(s).
这个小组男生的平均成绩是14.8s.
归纳小结
1、数学来源于生活,又服务于生活,数学在生活中无处不在.
2、会用数学去解决生活中的变化现象,对于几次连续变化情况可以用有理数的加减法去解决.
3、很多实际问题可以转化为有理数的加减混合运算来解决.
挑战自我,思维拓展
1、如图是5个城市的国际标准时间(单位:时),若北京时间是2019年11月20日上午11时时,那么(
)
A、首尔时间是2019年11月20日上午10时
B、伦敦时间是2019年11月20日凌晨3时
C、多伦多时间是2019年11月19日晚22时
D、纽约时间是2019年11月19日晚20时
B
-5
-4
0
8
9
北
京
首尔
伦敦
多伦多
纽约
2、某公交车原坐有22人,经过4个站点时,上下车情况记录如下(上车为正,下车为负):+4,-8,+6,-5,+2,-3,+1,-7.则车上还有(
)
A、36人
B、
32人
C、
22人
D、
12人
C
3、如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这点开始跳,则经2019次跳后它停在的点所对应的数为( )
A.1
B.2
C.3
D.5
D
4、我国著名的“五岳”海拔高度为:东岳泰山1532米,西岳华山2154.9米,南岳衡山1300.2米,北岳恒山2016.1米,中岳嵩山1491.7米.若以西岳华山的海拔高度为0点,则东岳泰山的高度是
(
)
A、1545米
B、2160米
C、615米
D、-622.9米
D
5、潜水艇上升为正,下降为负,若潜水艇先在距离水面65m深处,两次记录情况分别是-15m,19m,那么此时潜水艇在距水面
深处.
6、A、B、C三点相对海平面分别是-15米、-8.5米、-19米,那么这三点中最高的地方比最低的地方高
米.
61m
10.5
7.一口深4.8米的深井,一只青蛙从井底沿井壁往上爬,第一次爬了1.76米又下滑了0.37米,第二次往上爬了0.72米又下滑了0.27米,第三次往上爬了1.64米又下滑了0.48米,第四次往上爬了0.85米又下滑了0.23米,第五次往上爬了0.96米.
问题:小青蛙爬出井了吗?
解:4.8-(1.76-0.37+0.72-0.27+1.64-0.48+0.85-0.23+0.96)=0.22>0
,
所以小青蛙没有爬出井口.
8.先阅读下面的问题:在实际生活中常见到求平均数的问题.例如:为了了解某路公交车高峰时段从总站乘车出行的人数,随机抽查了10个班次的乘车人数,结果如下:24,28
,29
,25
,27
,28
,29
,26,
21
,23求这10个班次乘车人数的平均数.解:分别将各数减去25,得-1,+3,+4,0,+2,+3,+4,+1,-4,-2这组数的平均数为:(-1+3+4+0+2+3+4+1-4-2)÷10=10÷10=1则已知数据的平均数为:25+1=26答:这10个班次乘车人数的平均数为26.
通过阅读上面解决问题的方法,请利用它解决下面的问题:
(1)10筐西红柿称重(千克)如下:51,48,49,52.5,52,51.5,50,48.5,52,48.5问这10筐苹果的平均重量是多少?
(2)若有一组数为:2a+1,2a+3,2a-2.5,2a-3.5,2a-1,2a+5,2a-2,这组数的平均数为______.
解:(1)分别将各数减去以50,得+1,-2,-1,+2.5,+2,+1.5,0,-1.5,+2,-1.5.
由题意可得:+1-2-1+2.5+2+1.5+0-1.5+2-1.5=3,
则原数据的平均数=50+3÷10=50.3(kg);
答:10筐西红柿的平均重量是50.3kg;
(2)分别将各数减去以2a,得+1、+3、-2.5、-3.5、-1、+5、-2,则+1+3-2.5-3.5-1+5-2=
0,
则已知数据的平均数为2a+0=2a.
答:平均数为2a.
别忘记了作业
北师大版
初中数学
北师大版七年级数学(上册)
第二章
有理数及其运算
2.6有理数的加减混合运算
第三课时
学习目标
1.熟悉在水位变化过程中出现的量,进一步加深对有理数意义的理解,巩固有理数在实际生活中的作用.
2.能综合运用有理数及其加减法的有关知识,解决简单的实际问题,体会数学与现实生活的联系.
温故而知新
2.减法可以转化为加法,再写成代数和的形式,
如(-12)+(-5)-(-7)-(+6)=
.
1.加法分为
和
相加,关键在于确定
.
正
负
-12-5+7-6
确定符号
某电动自行车制造厂计划前半年内每月生产汽车360辆,由于另有任务,每月上班人数有变化,1月至6月实际每月生产量和计划每月生产量相比,变化情况如下(增加为正,减少为负,单位:辆):
+5,-3,-2,+7,+1,-6.
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
解:(1)(+7)-(-6)=13(辆).
故生产量最多的一个月比生产量最少的一个月多生产了13辆;
导入新课
(2)前半年的实际总产量是多少?比计划的总产量多了还是少了?相差多少?
解:(2)前半年实际总产量为
(+5)+(-3)+(-2)+(+7)+(+1)+(-6)
=+2(辆).
所以比原计划的总产量多了2辆.
右图是流花河的水文资料(单位:m)如果取河流的警戒水位
为0点,那么图中的其它数据可以记作什么?
解:最高水位可以记作:35.3-33.4=+1.9(m).
平均水位可以记作:22.6-33.4=-10.8(m).
最低水位可以记作:11.5-33.4=-21.9(m).
探究新知
下表是今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位)
星
期
一
二
三
四
五
六
七
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?本周哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
合作探究
(1)本周哪一天河流的水位最高?本周哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
解:本周每天水位记录为:
周一:33.4+0.20=33.6(m)
周二:33.4+0.20+0.81=34.41(m)
周三:33.4+0.20+0.81-0.35=34.06(m)
周四:33.4+0.20+0.81-0.35+0.03=34.09(m)
周五:33.4+0.20+0.81-0.35+0.03+0.28=34.37(m)
周六:33.4+0.20+0.81-0.35+0.03+0.28-0.36=34.01(m)
周日:33.4+0.20+0.81-0.35+0.03+0.28-0.36-0.01=34.00(m)
所以周二的水位最高,周一的水位最低;
它们都在警戒水位以上,
其中,最高水位与警戒水位的距离是34.41-33.4=1.01(m)
或0.20+0.81=1.01(m),
最低水位与警戒水位的距离是33.6-33.4=0.2(m).
(2)与上周末相比,本周末河流水位是上升了还是下降了?
解:上周末的水位记录为33.4m,
本周末的水位记录为34.00m,
与周末相比,本周末的水位是上升了.
(3)完成下面的本周水位记录表:
星
期
一
二
三
四
五
六
七
水位记录/m
33.6
34.00
33.41
34.06
34.09
34.37
34.01
(4)以警戒水位为0点,用折线统计图表示本周的水位情况.
某校八年级1班的所有男同学进行了100米跑步测试,达标成绩为15s,下表是某小组7名男生的成绩记录(单位:s)
注:正数表示成绩大于15s,负数表示成绩小于15s.
(1)这七名同学中编号为多少的成绩最高?成绩是多少s?
解:(1)编号为3的同学的成绩最高,
15-1.2=13.8(s);
例题解析
编号
1
2
3
4
5
6
7
8
成绩(s)
-0.8
+1
-1.2
0
-0.7
+0.6
-0.4
-0.1
(2)这个小组男生的达标率是多少?
解:(2)根据题意,可知成绩即为正数的不达标,故有2人不达标,6人达标,
所以这个小组男生的达标率是6÷8×100%=75%.
(3)这个小组男生的平均成绩是多少?
(-0.8)+(+1)+(-1.2)+(0)+(-0.7)+(+0.6)+(-0.4)+(-0.1)=-1.6(s)
15-1.6÷8=14.8(s).
这个小组男生的平均成绩是14.8s.
归纳小结
1、数学来源于生活,又服务于生活,数学在生活中无处不在.
2、会用数学去解决生活中的变化现象,对于几次连续变化情况可以用有理数的加减法去解决.
3、很多实际问题可以转化为有理数的加减混合运算来解决.
挑战自我,思维拓展
1、如图是5个城市的国际标准时间(单位:时),若北京时间是2019年11月20日上午11时时,那么(
)
A、首尔时间是2019年11月20日上午10时
B、伦敦时间是2019年11月20日凌晨3时
C、多伦多时间是2019年11月19日晚22时
D、纽约时间是2019年11月19日晚20时
B
-5
-4
0
8
9
北
京
首尔
伦敦
多伦多
纽约
2、某公交车原坐有22人,经过4个站点时,上下车情况记录如下(上车为正,下车为负):+4,-8,+6,-5,+2,-3,+1,-7.则车上还有(
)
A、36人
B、
32人
C、
22人
D、
12人
C
3、如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这点开始跳,则经2019次跳后它停在的点所对应的数为( )
A.1
B.2
C.3
D.5
D
4、我国著名的“五岳”海拔高度为:东岳泰山1532米,西岳华山2154.9米,南岳衡山1300.2米,北岳恒山2016.1米,中岳嵩山1491.7米.若以西岳华山的海拔高度为0点,则东岳泰山的高度是
(
)
A、1545米
B、2160米
C、615米
D、-622.9米
D
5、潜水艇上升为正,下降为负,若潜水艇先在距离水面65m深处,两次记录情况分别是-15m,19m,那么此时潜水艇在距水面
深处.
6、A、B、C三点相对海平面分别是-15米、-8.5米、-19米,那么这三点中最高的地方比最低的地方高
米.
61m
10.5
7.一口深4.8米的深井,一只青蛙从井底沿井壁往上爬,第一次爬了1.76米又下滑了0.37米,第二次往上爬了0.72米又下滑了0.27米,第三次往上爬了1.64米又下滑了0.48米,第四次往上爬了0.85米又下滑了0.23米,第五次往上爬了0.96米.
问题:小青蛙爬出井了吗?
解:4.8-(1.76-0.37+0.72-0.27+1.64-0.48+0.85-0.23+0.96)=0.22>0
,
所以小青蛙没有爬出井口.
8.先阅读下面的问题:在实际生活中常见到求平均数的问题.例如:为了了解某路公交车高峰时段从总站乘车出行的人数,随机抽查了10个班次的乘车人数,结果如下:24,28
,29
,25
,27
,28
,29
,26,
21
,23求这10个班次乘车人数的平均数.解:分别将各数减去25,得-1,+3,+4,0,+2,+3,+4,+1,-4,-2这组数的平均数为:(-1+3+4+0+2+3+4+1-4-2)÷10=10÷10=1则已知数据的平均数为:25+1=26答:这10个班次乘车人数的平均数为26.
通过阅读上面解决问题的方法,请利用它解决下面的问题:
(1)10筐西红柿称重(千克)如下:51,48,49,52.5,52,51.5,50,48.5,52,48.5问这10筐苹果的平均重量是多少?
(2)若有一组数为:2a+1,2a+3,2a-2.5,2a-3.5,2a-1,2a+5,2a-2,这组数的平均数为______.
解:(1)分别将各数减去以50,得+1,-2,-1,+2.5,+2,+1.5,0,-1.5,+2,-1.5.
由题意可得:+1-2-1+2.5+2+1.5+0-1.5+2-1.5=3,
则原数据的平均数=50+3÷10=50.3(kg);
答:10筐西红柿的平均重量是50.3kg;
(2)分别将各数减去以2a,得+1、+3、-2.5、-3.5、-1、+5、-2,则+1+3-2.5-3.5-1+5-2=
0,
则已知数据的平均数为2a+0=2a.
答:平均数为2a.
别忘记了作业
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
