华师大版七年级上册数学第5章 相交线与平行线解答题能力突破与提升专项练习(无答案)
文档属性
| 名称 | 华师大版七年级上册数学第5章 相交线与平行线解答题能力突破与提升专项练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 20:19:13 | ||
图片预览

文档简介
华师大版七年级上册数学《相交线与平行线》解答题
能力突破与提升专项练习
一.相交线部分:
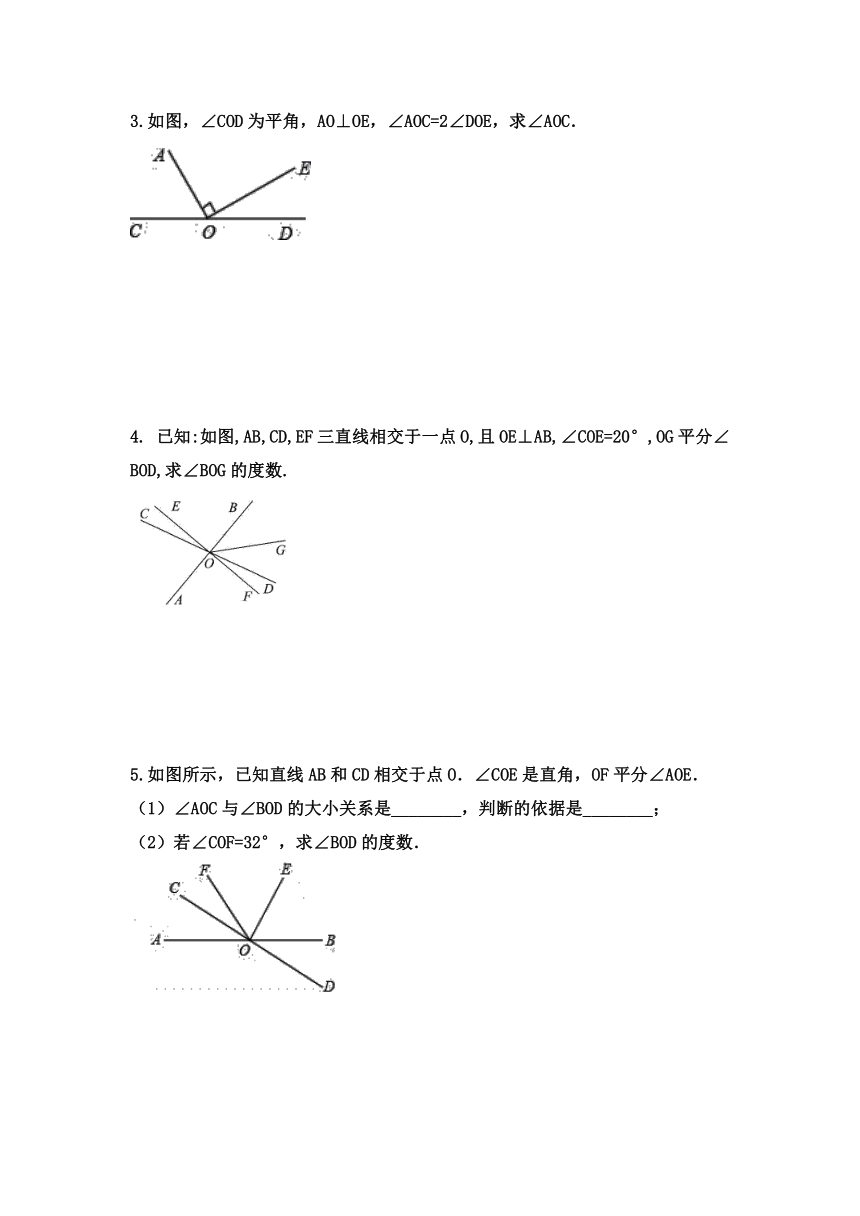
1.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?
2.如图,直线AB,CD相交于点O.写出∠1,∠2,∠3,∠4中每两个角之间的位置关系.
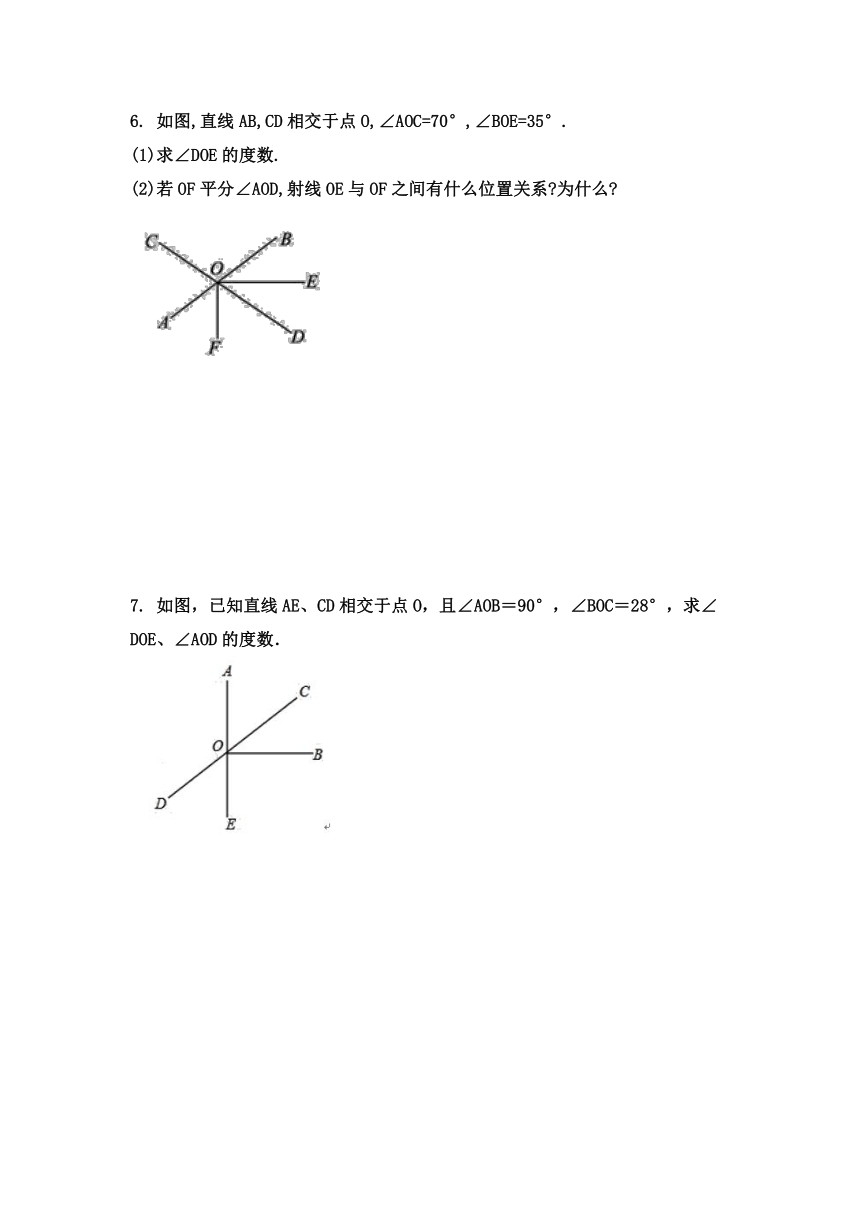
3.如图,∠COD为平角,AO⊥OE,∠AOC=2∠DOE,求∠AOC.
4.
已知:如图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
5.如图所示,已知直线AB和CD相交于点O.∠COE是直角,OF平分∠AOE.
(1)∠AOC与∠BOD的大小关系是________,判断的依据是________;
(2)若∠COF=32°,求∠BOD的度数.
6.
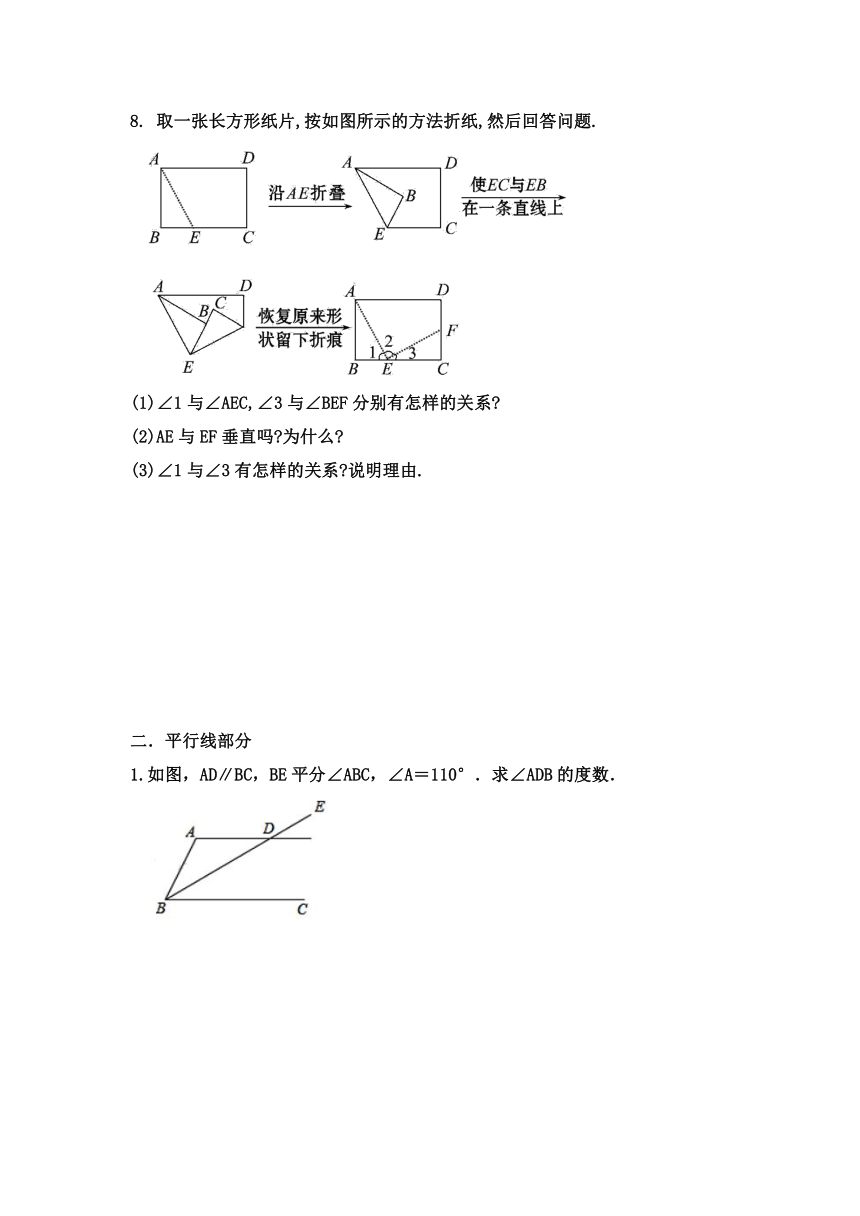
如图,直线AB,CD相交于点O,∠AOC=70°,∠BOE=35°.
(1)求∠DOE的度数.
(2)若OF平分∠AOD,射线OE与OF之间有什么位置关系?为什么?
7.
如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠
DOE、∠AOD的度数.
8.
取一张长方形纸片,按如图所示的方法折纸,然后回答问题.
(1)∠1与∠AEC,∠3与∠BEF分别有怎样的关系?
(2)AE与EF垂直吗?为什么?
(3)∠1与∠3有怎样的关系?说明理由.
二.平行线部分
1.如图,AD∥BC,BE平分∠ABC,∠A=110°.求∠ADB的度数.
2.
如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
3.
如图,已知∠1=∠2,∠3+∠4=180°,请说明AB∥EF的理由.
.
4.如图,直线MN分别交AB和CD于点E、F,点Q在PM上,∠EPM=∠FQM,且∠AEP=∠CFQ,试说明:AB∥CD.
5.如图,∠1+∠2=180°,∠DEF=∠A,∠BED=70°.
(1)试说明:EF∥AB;
(2)求∠ACB的度数.
6.如图,直线EF交直线AB、CD与点M、N,NP平分∠ENC交直线AB于点
P.已知∠EMB=112°,∠PNC=34°.
(1)求证:AB∥CD;
(2)若PQ将分∠APN成两部分,且∠APQ:∠QPN=1:3,求∠PQD的度数.
7.如图1,已知AB∥CD,∠B=30°,∠D=120°;
(1)若∠E=60°,则∠F=_____;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
8.完成下列证明过程,并在括号内填上依据.
如图,点E在AB边上,点F在CD边上,∠1=∠2,∠B=∠C,试说明AB∥CD.
解:∵∠1=∠2(已知),∠1=∠4(
),
∴∠2=
(等量代换),
∴
∥BF(
),
∴∠3=∠
(
).
又∵∠B=∠C(已知),
∴∠3=∠B(
),
∴AB∥CD(
).
9.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
10.已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
(1)如图①,若∠A=20°,∠C=40°,则∠AEC=
°;
(2)如图②,若∠A=x°,∠C=y°,则∠AEC=
°;
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
能力突破与提升专项练习
一.相交线部分:
1.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?
2.如图,直线AB,CD相交于点O.写出∠1,∠2,∠3,∠4中每两个角之间的位置关系.
3.如图,∠COD为平角,AO⊥OE,∠AOC=2∠DOE,求∠AOC.
4.
已知:如图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
5.如图所示,已知直线AB和CD相交于点O.∠COE是直角,OF平分∠AOE.
(1)∠AOC与∠BOD的大小关系是________,判断的依据是________;
(2)若∠COF=32°,求∠BOD的度数.
6.
如图,直线AB,CD相交于点O,∠AOC=70°,∠BOE=35°.
(1)求∠DOE的度数.
(2)若OF平分∠AOD,射线OE与OF之间有什么位置关系?为什么?
7.
如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠
DOE、∠AOD的度数.
8.
取一张长方形纸片,按如图所示的方法折纸,然后回答问题.
(1)∠1与∠AEC,∠3与∠BEF分别有怎样的关系?
(2)AE与EF垂直吗?为什么?
(3)∠1与∠3有怎样的关系?说明理由.
二.平行线部分
1.如图,AD∥BC,BE平分∠ABC,∠A=110°.求∠ADB的度数.
2.
如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
3.
如图,已知∠1=∠2,∠3+∠4=180°,请说明AB∥EF的理由.
.
4.如图,直线MN分别交AB和CD于点E、F,点Q在PM上,∠EPM=∠FQM,且∠AEP=∠CFQ,试说明:AB∥CD.
5.如图,∠1+∠2=180°,∠DEF=∠A,∠BED=70°.
(1)试说明:EF∥AB;
(2)求∠ACB的度数.
6.如图,直线EF交直线AB、CD与点M、N,NP平分∠ENC交直线AB于点
P.已知∠EMB=112°,∠PNC=34°.
(1)求证:AB∥CD;
(2)若PQ将分∠APN成两部分,且∠APQ:∠QPN=1:3,求∠PQD的度数.
7.如图1,已知AB∥CD,∠B=30°,∠D=120°;
(1)若∠E=60°,则∠F=_____;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
8.完成下列证明过程,并在括号内填上依据.
如图,点E在AB边上,点F在CD边上,∠1=∠2,∠B=∠C,试说明AB∥CD.
解:∵∠1=∠2(已知),∠1=∠4(
),
∴∠2=
(等量代换),
∴
∥BF(
),
∴∠3=∠
(
).
又∵∠B=∠C(已知),
∴∠3=∠B(
),
∴AB∥CD(
).
9.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
10.已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
(1)如图①,若∠A=20°,∠C=40°,则∠AEC=
°;
(2)如图②,若∠A=x°,∠C=y°,则∠AEC=
°;
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
