江西省赣州市赣县区第三中学2020-2021学年高二(零班,奥数班)九月月考数学(理)试卷(Word含答案)
文档属性
| 名称 | 江西省赣州市赣县区第三中学2020-2021学年高二(零班,奥数班)九月月考数学(理)试卷(Word含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 00:00:00 | ||
图片预览



文档简介
江西省赣州市赣县区第三中学2020-2021学年高二
(零班,奥数班)九月月考数学(理)试卷
一、单选题
1.若直线与平行,则与间的距离为(
)
A.
B.
C.
D.
2.某单位有840名职工,
现采用系统抽样方法,
抽取42人做问卷调查,
将840人按1,
2,
…,
840随机编号,
则抽取的42人中,
编号落入区间[481,
720]的人数为
(
)
A.11
B.12
C.13
D.14
3.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )
A.
B.
C.
D.
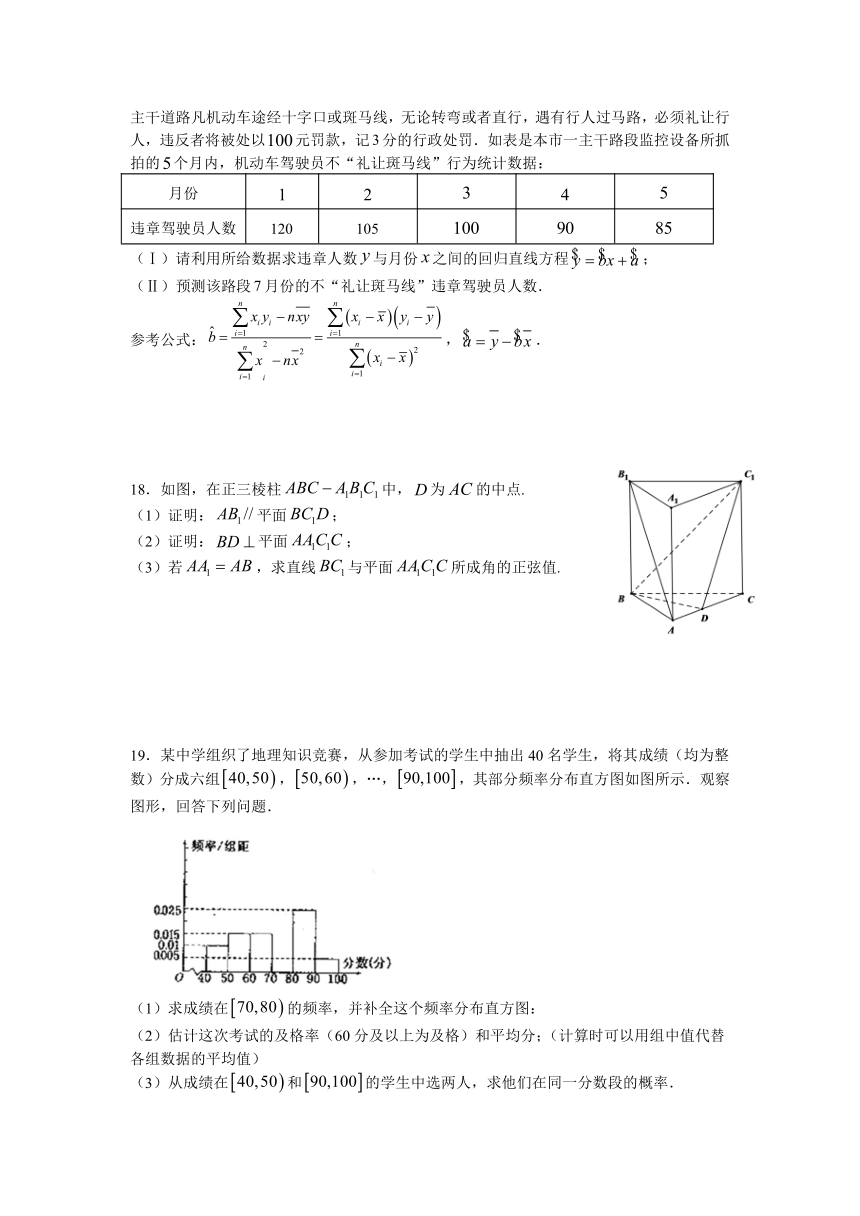
4.某中学2019年的高考考生人数是2016年高考考生人数的倍,为了更好地对比该校考生的升学情况,统计了核校2016年和2019年的高考情况,得到如图柱状图:
则下列结论正确的是(
)
A.与2016年相比,2019年一本达线人数减少
B.与2016年相比,2019年二本达线人数增加了倍
C.2016年与2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
5.已知直线、,平面、,给出下列命题:
①若,,且,则
②若,,且,则
③若,,且,则
④若,,且,则
其中正确的命题是(
)
A.②③
B.①③
C.①④
D.③④
6.如图所示,在正方体中,,分别是,的中点,则直线与所成角的余弦值是(
)
A.
B.
C.
D.
7.执行如图所示的程序框图,如果输入的是10,那么输出的是(
)
A.2
B.
C.
D.
8.若直线ax+2by-2=0(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则+的最小值为(
)
A.1
B.5
C.4
D.3+2
9.等比数列的各项均为正数,且,则(
)
A.8
B.10
C.12
D.14
10.过点作圆的最短弦,则这条弦所在直线的方程是(
)
A.
B.
C.
D.
11.某几何体的三视图如图所示,则该几何体的表面积为(
)
A.
B.
C.
D.
12.在中,角、、的对边分别为、、,已知且,则的最小值为( )
A.
B.2
C.
D.4
二、填空题
13.直线与直线垂直,且它在轴上的截距为4,则直线的方程为_______.
14.在边长为2的正内任取一点,则点到三个顶点的距离都不小于1的概率为________.
15.如图,在三棱锥中,,,,且,,则二面角的余弦值是_____.
16.已知球面上有四点,,,,,且平面,则此球的体积为______________.
三、解答题
17.平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以元罚款,记分的行政处罚.如表是本市一主干路段监控设备所抓拍的个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份
违章驾驶员人数
(Ⅰ)请利用所给数据求违章人数与月份之间的回归直线方程;
(Ⅱ)预测该路段月份的不“礼让斑马线”违章驾驶员人数.
参考公式:,.
18.如图,在正三棱柱中,为的中点.
(1)证明:平面;
(2)证明:平面;
(3)若,求直线与平面所成角的正弦值.
19.某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组,,…,,其部分频率分布直方图如图所示.观察图形,回答下列问题.
(1)求成绩在的频率,并补全这个频率分布直方图:
(2)估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)
(3)从成绩在和的学生中选两人,求他们在同一分数段的概率.
20.在中,内角所对的边分别为
,且的面积满足.
(1)求角的值;
(2)若边上的中线长为,求的值.
21.已知四边形是梯形(如图1),,,,,E为的中点,以为折痕把折起,使点D到达点P的位置(如图2),且.
(1)求证:平面平面;
(2)求点C到平面的距离.
22.已知圆与直线相切于点,圆心在轴上.
(1)求圆的方程;
(2)过点且不与轴重合的直线与圆相交于两点,为坐标原点,直线分别与直线相交于两点,记的面积分别是.求的取值范围.
答案
1.B
2.B
3.B
4.D
5.C
6.C
7.C
8.D
9.A
10.D
11.D
12.A
由可知,,解得,
由基本不等式得,.,
令,则,,
,在,上单调递增,
(4),即的最小值为.
13.
14.
15.
16.
解:设的外心为,则三棱锥的外接球的球心在过点,垂直于平面的平面的直线,设球心为,的外接圆半径为,设外接球的半径为,
因为,,,所以,
所以,由正弦定理得,,所以,
因为平面,,所以,
所以外接球的体积为
17.(Ⅰ);(Ⅱ)人.
解:(Ⅰ)由表中数据,计算;,,
,
所以与之间的回归直线方程为;
(Ⅱ)时,,
18.(1)证明见解析;(2)证明见解析;(3).
(1)证明:连接,交于点,连接.
因为为矩形,则为的中点;
因为为的中点,所以,
又因为平面,平面,所以平面.
(2)在正三棱柱中,
因为平面,平面,所以.
因为为等边三角形,为的中点,所以.
又因为,平面,所以平面;
(3)由(2)知,平面,所以
即为直线与平面所成的角,
设等边的边长为2,则,
所以在中,,,所以.
即直线与平面所成的角的正弦值为.
19.(1)0.3
(2)75%;71
(3)
(1)因为各组的频率之和等于1,所以成绩在的频率为。
补全频率分布直方图如图所示:
(2)根据题意,60分及以上的分数在,,,这四个组,其频率之和为,故本次考试的及格率为75%
利用中值估算学生成绩的平均分,则有
所以本次考试的平均分为71分。
(3)成绩在的人数为人,成绩在的人数为人
从成绩在和的学生中选两人,将分数段的4人编号为,,,,将分数段的2人编号为,,从中任选两人,则基本事件构成集合
共15个,其中同一分数段内所含基本事件为:
,,,,,,共7个,故概率
20.(1);(2).
解:(1)根据三角形面积公式得:,
又因为,∴
,∵
,∴.
(2)由(1)得,设的中点为,则,
∵
,∴
∴
,∴
根据余弦定理得:得,解得.
21.(1)证明见解析;(2).
(1)证明:连接,
因为,,,E为的中点,,
所以四边形是边长为1的正方形,且.
如图,取的中点M,连接,,,
因为,所以,且,.
因为,所以.
所以
因为,,,所以,所以.
因为,所以平面.
因为平面,所以平面平面.
(2)由(1)知,平面,,且.
因为,所以为正三角形且边长为1.
设点C到平面的距离为d,则,
所以,
即,解得.
所以点C到平面的距离为.
22.(1);
(2).
(1)由题可知,设圆的方程为,
,解得,,所以圆的方程为.
(2)由题意知,,
设直线的斜率为
,则直线的方程为,
由,得,解得或,则点的坐标为.
又直线的斜率为,同理可得点的坐标为.
由题可知,,.
因此,
又,同理,
所以,当且仅当时取等号.
又,所以的取值范围是.
(零班,奥数班)九月月考数学(理)试卷
一、单选题
1.若直线与平行,则与间的距离为(
)
A.
B.
C.
D.
2.某单位有840名职工,
现采用系统抽样方法,
抽取42人做问卷调查,
将840人按1,
2,
…,
840随机编号,
则抽取的42人中,
编号落入区间[481,
720]的人数为
(
)
A.11
B.12
C.13
D.14
3.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )
A.
B.
C.
D.
4.某中学2019年的高考考生人数是2016年高考考生人数的倍,为了更好地对比该校考生的升学情况,统计了核校2016年和2019年的高考情况,得到如图柱状图:
则下列结论正确的是(
)
A.与2016年相比,2019年一本达线人数减少
B.与2016年相比,2019年二本达线人数增加了倍
C.2016年与2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
5.已知直线、,平面、,给出下列命题:
①若,,且,则
②若,,且,则
③若,,且,则
④若,,且,则
其中正确的命题是(
)
A.②③
B.①③
C.①④
D.③④
6.如图所示,在正方体中,,分别是,的中点,则直线与所成角的余弦值是(
)
A.
B.
C.
D.
7.执行如图所示的程序框图,如果输入的是10,那么输出的是(
)
A.2
B.
C.
D.
8.若直线ax+2by-2=0(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则+的最小值为(
)
A.1
B.5
C.4
D.3+2
9.等比数列的各项均为正数,且,则(
)
A.8
B.10
C.12
D.14
10.过点作圆的最短弦,则这条弦所在直线的方程是(
)
A.
B.
C.
D.
11.某几何体的三视图如图所示,则该几何体的表面积为(
)
A.
B.
C.
D.
12.在中,角、、的对边分别为、、,已知且,则的最小值为( )
A.
B.2
C.
D.4
二、填空题
13.直线与直线垂直,且它在轴上的截距为4,则直线的方程为_______.
14.在边长为2的正内任取一点,则点到三个顶点的距离都不小于1的概率为________.
15.如图,在三棱锥中,,,,且,,则二面角的余弦值是_____.
16.已知球面上有四点,,,,,且平面,则此球的体积为______________.
三、解答题
17.平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以元罚款,记分的行政处罚.如表是本市一主干路段监控设备所抓拍的个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份
违章驾驶员人数
(Ⅰ)请利用所给数据求违章人数与月份之间的回归直线方程;
(Ⅱ)预测该路段月份的不“礼让斑马线”违章驾驶员人数.
参考公式:,.
18.如图,在正三棱柱中,为的中点.
(1)证明:平面;
(2)证明:平面;
(3)若,求直线与平面所成角的正弦值.
19.某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组,,…,,其部分频率分布直方图如图所示.观察图形,回答下列问题.
(1)求成绩在的频率,并补全这个频率分布直方图:
(2)估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)
(3)从成绩在和的学生中选两人,求他们在同一分数段的概率.
20.在中,内角所对的边分别为
,且的面积满足.
(1)求角的值;
(2)若边上的中线长为,求的值.
21.已知四边形是梯形(如图1),,,,,E为的中点,以为折痕把折起,使点D到达点P的位置(如图2),且.
(1)求证:平面平面;
(2)求点C到平面的距离.
22.已知圆与直线相切于点,圆心在轴上.
(1)求圆的方程;
(2)过点且不与轴重合的直线与圆相交于两点,为坐标原点,直线分别与直线相交于两点,记的面积分别是.求的取值范围.
答案
1.B
2.B
3.B
4.D
5.C
6.C
7.C
8.D
9.A
10.D
11.D
12.A
由可知,,解得,
由基本不等式得,.,
令,则,,
,在,上单调递增,
(4),即的最小值为.
13.
14.
15.
16.
解:设的外心为,则三棱锥的外接球的球心在过点,垂直于平面的平面的直线,设球心为,的外接圆半径为,设外接球的半径为,
因为,,,所以,
所以,由正弦定理得,,所以,
因为平面,,所以,
所以外接球的体积为
17.(Ⅰ);(Ⅱ)人.
解:(Ⅰ)由表中数据,计算;,,
,
所以与之间的回归直线方程为;
(Ⅱ)时,,
18.(1)证明见解析;(2)证明见解析;(3).
(1)证明:连接,交于点,连接.
因为为矩形,则为的中点;
因为为的中点,所以,
又因为平面,平面,所以平面.
(2)在正三棱柱中,
因为平面,平面,所以.
因为为等边三角形,为的中点,所以.
又因为,平面,所以平面;
(3)由(2)知,平面,所以
即为直线与平面所成的角,
设等边的边长为2,则,
所以在中,,,所以.
即直线与平面所成的角的正弦值为.
19.(1)0.3
(2)75%;71
(3)
(1)因为各组的频率之和等于1,所以成绩在的频率为。
补全频率分布直方图如图所示:
(2)根据题意,60分及以上的分数在,,,这四个组,其频率之和为,故本次考试的及格率为75%
利用中值估算学生成绩的平均分,则有
所以本次考试的平均分为71分。
(3)成绩在的人数为人,成绩在的人数为人
从成绩在和的学生中选两人,将分数段的4人编号为,,,,将分数段的2人编号为,,从中任选两人,则基本事件构成集合
共15个,其中同一分数段内所含基本事件为:
,,,,,,共7个,故概率
20.(1);(2).
解:(1)根据三角形面积公式得:,
又因为,∴
,∵
,∴.
(2)由(1)得,设的中点为,则,
∵
,∴
∴
,∴
根据余弦定理得:得,解得.
21.(1)证明见解析;(2).
(1)证明:连接,
因为,,,E为的中点,,
所以四边形是边长为1的正方形,且.
如图,取的中点M,连接,,,
因为,所以,且,.
因为,所以.
所以
因为,,,所以,所以.
因为,所以平面.
因为平面,所以平面平面.
(2)由(1)知,平面,,且.
因为,所以为正三角形且边长为1.
设点C到平面的距离为d,则,
所以,
即,解得.
所以点C到平面的距离为.
22.(1);
(2).
(1)由题可知,设圆的方程为,
,解得,,所以圆的方程为.
(2)由题意知,,
设直线的斜率为
,则直线的方程为,
由,得,解得或,则点的坐标为.
又直线的斜率为,同理可得点的坐标为.
由题可知,,.
因此,
又,同理,
所以,当且仅当时取等号.
又,所以的取值范围是.
同课章节目录
