江西省赣州市赣县区第三中学2020-2021学年高二(零班,奥数班)九月月考数学(文)试卷(Word含答案)
文档属性
| 名称 | 江西省赣州市赣县区第三中学2020-2021学年高二(零班,奥数班)九月月考数学(文)试卷(Word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 986.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 00:00:00 | ||
图片预览



文档简介
江西省赣州市赣县区第三中学2020-2021学年高二
(零班,奥数班)九月月考数学(文)试卷
一、单选题
1.某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数为( )
A.7
B.8
C.9
D.10
2.已知等比数列满足,,则(
)
A.
B.
C.
D.
3.若点关于平面的对称点为,点关于轴对称点为,点为线段的中点,则(
)
A.
B.
C.5
D.
4.四棱锥的三视图如图所示,则异面直线与所成的角的余弦值为(
)
B.
C.
D.
5.在正方体中,E,F,G分别为,BC,的中点,现有下面三个结论:①为正三角形;②异面直线与所成角为,③平面EFG;④过A作平面,使得棱AD,,在平面的正投影的长度相等,则这样的平面有4个.则所有正确编号是(
)
A.②④
B.②③
C.①③
D.①③④
6.从分别写有的张卡片中随机抽取张,放回后再随机抽取张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为(
)
A.
B.
C.
D.
7.已知P是△ABC所在平面内﹣点,,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
A.
B.
C.
D.
8.若函数的图象与直线有公共点,则实数的取值范围为(
)
A.
B..
C.
D.
9.执行如图所示的程序框图,输出的结果为
B.
C.
D.
10.已知直线y=x+m和圆x2+y2=1交于A、B两点,O为坐标原点,若,则实数m=( )
A.
B.
C.
D.
11.如图所示,在棱长为的正方体中,是棱的中点,是侧面上的动点,且面,则在侧面上的轨迹的长度是
A.
B.
C.
D.
12.已知圆,圆,分别为圆和圆上的动点,为直线上的动点,则的最小值为
A.
B.
C.
D.
二、填空题
13.设满足约束条件,则的最小值为__________.
14.总体由编号为的个个体组成,利用随机数表(以下选取了随机数表中的第行和第行)选取个个体,选取方法是从随机数表第行的第列开始由左向右读取,则选出来的第个个体的编号为______.
15.已知对一切上恒成立,则实数a的取值范围是____.
16.如图,中,,,的面积为,
点在内,且,则的面积的最大值为____
.
三、解答题
17.已知点,圆.
(1)求过点且与圆相切的直线方程;
(2)若直线与圆相交于,两点,且弦的长为,求实数的值.
18.△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB.
(Ⅰ)求B;
(Ⅱ)若b=2,求△ABC面积的最大值.
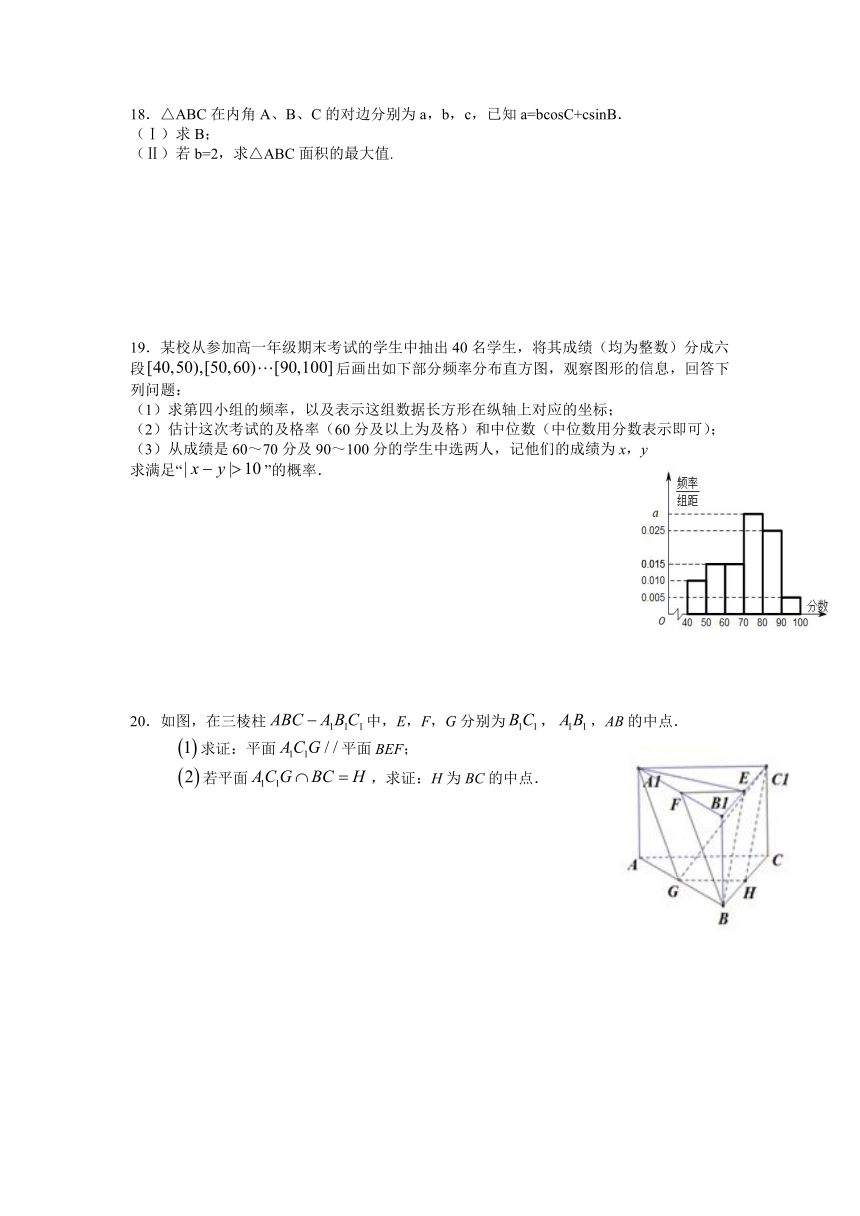
19.某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率,以及表示这组数据长方形在纵轴上对应的坐标;
(2)估计这次考试的及格率(60分及以上为及格)和中位数(中位数用分数表示即可);
(3)从成绩是60~70分及90~100分的学生中选两人,记他们的成绩为x,y
求满足“”的概率.
20.如图,在三棱柱中,E,F,G分别为,,AB的中点.
求证:平面平面BEF;
若平面,求证:H为BC的中点.
21.已知首项为的等差数列中,是的等比中项.
(1)
求数列的通项公式;
(2)
若数列是单调数列,且数列满足,求数列的前项和.
22.在平面直角坐标系中,已知直线∶和圆∶,是直线上一点,过点作圆的两条切线,切点分别为.
(1)若,求点坐标;
(2)若圆上存在点,使得,求点的横坐标的取值范围;
(3)设线段的中点为,与轴的交点为,求线段长的最大值.
答案
1.D
2.C
3.C
4.A
5.D
6.D
7.B
8.B
9.C
10.C
11.D
12.A
由圆,圆,
可知圆圆心为,半经为1,如图,
圆圆心为,半经为2,
圆关于直线的对称圆为圆,
连结,交于,则为满足使最小的点,
此时点为与圆的交点关于直线对称的点,为与圆的交点,
最小值为,
而,
的最小值为,故选A.
13.-5
14、43
15、.
16.
17.(1)由圆的方程得到圆心,半径.
当直线斜率不存在时,直线与圆显然相切;
当直线斜率存在时,设所求直线方程为,即,
由题意得:,解得,
∴
方程为,即.
故过点且与圆相切的直线方程为或.
(2)∵
弦长为,半径为2.
圆心到直线的距离,∴,解得.
18.(1)∵a=bcosC+csinB
∴由正弦定理知sinA=sinBcosC+sinCsinB
①
在三角形ABC中,A=-(B+C)
∴sinA=sin(B+C)=sinBcosC+cosBsinC
②
由①和②得sinBsinC=cosBsinC
而C∈(0,),∴sinC≠0,∴sinB=cosB
又B(0,),∴B=
(2)
S△ABCacsinBac,
由已知及余弦定理得:4=a2+c2﹣2accos2ac﹣2ac,
整理得:ac,当且仅当a=c时,等号成立,
则△ABC面积的最大值为(2)1.
19.解:(1)由频率分布直方图可知第1,2,3,5,6小组的频率分别为:
0.1,0.15,0.15,0.25,0.05,
所以第4小组的频率为:.
∴在频率分布直方图中第4小组的对应的矩形的高,
(2)∵考试的及格率即60分及以上的频率
.
∴及格率为
∵
前三组的频率和为:,
∴
中位数为
(3)设“成绩满足”为事件A
由频率分布直方图可求得成绩在60~70分及90~100分的学生人数分别为6人和2人,
所以设60~70的6名学生分别为,90~100分的2名学生为,
则从这8个学生中选两人,所有可能情况为:
,共28种,且每种情况的出现均等可能,
若这2人成绩要满足“”,则要求一人选自60~70分数段,另一个选自90~100分数段,有如下情况:,共12种,
所以由古典概型概率公式有,
即所取2人的成绩满足“”的概率是.
20.如图,,F分别为,的中点,,
平面,平面,平面,
又F,G分别为,AB的中点,,
又,四边形为平行四边形,则,
平面,平面,平面,
又,平面平面BEF;
平面平面,平面平面,
平面与平面ABC有公共点G,则有经过G的直线,设交,
则,得,
为AB的中点,为BC的中点.
21.(1)
是的等比中项,是等差数列
或
或
(2)由(1)及是单调数列知
得
22.(1)若,则四边形为正方形,
则到圆心的距离为,
∵在直线上,设
故,解得,故;
(2)设,若圆上存在点,使得,
过作圆的切线,,∴,∴,
在直角三角形中,∵,
∴,即,∴,
∴,解得,
∴点横坐标的取值范围为:;
(3)设,则以为直径的圆的方程为
化简得,与联立,
可得所在直线方程:,
联立,得,
∴的坐标为,
可得点的轨迹为:,
圆心,半径.其中原点为极限点(也可以去掉).
由题意可知,∴.
∴.
∴线段的最大值为.
(零班,奥数班)九月月考数学(文)试卷
一、单选题
1.某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数为( )
A.7
B.8
C.9
D.10
2.已知等比数列满足,,则(
)
A.
B.
C.
D.
3.若点关于平面的对称点为,点关于轴对称点为,点为线段的中点,则(
)
A.
B.
C.5
D.
4.四棱锥的三视图如图所示,则异面直线与所成的角的余弦值为(
)
B.
C.
D.
5.在正方体中,E,F,G分别为,BC,的中点,现有下面三个结论:①为正三角形;②异面直线与所成角为,③平面EFG;④过A作平面,使得棱AD,,在平面的正投影的长度相等,则这样的平面有4个.则所有正确编号是(
)
A.②④
B.②③
C.①③
D.①③④
6.从分别写有的张卡片中随机抽取张,放回后再随机抽取张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为(
)
A.
B.
C.
D.
7.已知P是△ABC所在平面内﹣点,,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
A.
B.
C.
D.
8.若函数的图象与直线有公共点,则实数的取值范围为(
)
A.
B..
C.
D.
9.执行如图所示的程序框图,输出的结果为
B.
C.
D.
10.已知直线y=x+m和圆x2+y2=1交于A、B两点,O为坐标原点,若,则实数m=( )
A.
B.
C.
D.
11.如图所示,在棱长为的正方体中,是棱的中点,是侧面上的动点,且面,则在侧面上的轨迹的长度是
A.
B.
C.
D.
12.已知圆,圆,分别为圆和圆上的动点,为直线上的动点,则的最小值为
A.
B.
C.
D.
二、填空题
13.设满足约束条件,则的最小值为__________.
14.总体由编号为的个个体组成,利用随机数表(以下选取了随机数表中的第行和第行)选取个个体,选取方法是从随机数表第行的第列开始由左向右读取,则选出来的第个个体的编号为______.
15.已知对一切上恒成立,则实数a的取值范围是____.
16.如图,中,,,的面积为,
点在内,且,则的面积的最大值为____
.
三、解答题
17.已知点,圆.
(1)求过点且与圆相切的直线方程;
(2)若直线与圆相交于,两点,且弦的长为,求实数的值.
18.△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB.
(Ⅰ)求B;
(Ⅱ)若b=2,求△ABC面积的最大值.
19.某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率,以及表示这组数据长方形在纵轴上对应的坐标;
(2)估计这次考试的及格率(60分及以上为及格)和中位数(中位数用分数表示即可);
(3)从成绩是60~70分及90~100分的学生中选两人,记他们的成绩为x,y
求满足“”的概率.
20.如图,在三棱柱中,E,F,G分别为,,AB的中点.
求证:平面平面BEF;
若平面,求证:H为BC的中点.
21.已知首项为的等差数列中,是的等比中项.
(1)
求数列的通项公式;
(2)
若数列是单调数列,且数列满足,求数列的前项和.
22.在平面直角坐标系中,已知直线∶和圆∶,是直线上一点,过点作圆的两条切线,切点分别为.
(1)若,求点坐标;
(2)若圆上存在点,使得,求点的横坐标的取值范围;
(3)设线段的中点为,与轴的交点为,求线段长的最大值.
答案
1.D
2.C
3.C
4.A
5.D
6.D
7.B
8.B
9.C
10.C
11.D
12.A
由圆,圆,
可知圆圆心为,半经为1,如图,
圆圆心为,半经为2,
圆关于直线的对称圆为圆,
连结,交于,则为满足使最小的点,
此时点为与圆的交点关于直线对称的点,为与圆的交点,
最小值为,
而,
的最小值为,故选A.
13.-5
14、43
15、.
16.
17.(1)由圆的方程得到圆心,半径.
当直线斜率不存在时,直线与圆显然相切;
当直线斜率存在时,设所求直线方程为,即,
由题意得:,解得,
∴
方程为,即.
故过点且与圆相切的直线方程为或.
(2)∵
弦长为,半径为2.
圆心到直线的距离,∴,解得.
18.(1)∵a=bcosC+csinB
∴由正弦定理知sinA=sinBcosC+sinCsinB
①
在三角形ABC中,A=-(B+C)
∴sinA=sin(B+C)=sinBcosC+cosBsinC
②
由①和②得sinBsinC=cosBsinC
而C∈(0,),∴sinC≠0,∴sinB=cosB
又B(0,),∴B=
(2)
S△ABCacsinBac,
由已知及余弦定理得:4=a2+c2﹣2accos2ac﹣2ac,
整理得:ac,当且仅当a=c时,等号成立,
则△ABC面积的最大值为(2)1.
19.解:(1)由频率分布直方图可知第1,2,3,5,6小组的频率分别为:
0.1,0.15,0.15,0.25,0.05,
所以第4小组的频率为:.
∴在频率分布直方图中第4小组的对应的矩形的高,
(2)∵考试的及格率即60分及以上的频率
.
∴及格率为
∵
前三组的频率和为:,
∴
中位数为
(3)设“成绩满足”为事件A
由频率分布直方图可求得成绩在60~70分及90~100分的学生人数分别为6人和2人,
所以设60~70的6名学生分别为,90~100分的2名学生为,
则从这8个学生中选两人,所有可能情况为:
,共28种,且每种情况的出现均等可能,
若这2人成绩要满足“”,则要求一人选自60~70分数段,另一个选自90~100分数段,有如下情况:,共12种,
所以由古典概型概率公式有,
即所取2人的成绩满足“”的概率是.
20.如图,,F分别为,的中点,,
平面,平面,平面,
又F,G分别为,AB的中点,,
又,四边形为平行四边形,则,
平面,平面,平面,
又,平面平面BEF;
平面平面,平面平面,
平面与平面ABC有公共点G,则有经过G的直线,设交,
则,得,
为AB的中点,为BC的中点.
21.(1)
是的等比中项,是等差数列
或
或
(2)由(1)及是单调数列知
得
22.(1)若,则四边形为正方形,
则到圆心的距离为,
∵在直线上,设
故,解得,故;
(2)设,若圆上存在点,使得,
过作圆的切线,,∴,∴,
在直角三角形中,∵,
∴,即,∴,
∴,解得,
∴点横坐标的取值范围为:;
(3)设,则以为直径的圆的方程为
化简得,与联立,
可得所在直线方程:,
联立,得,
∴的坐标为,
可得点的轨迹为:,
圆心,半径.其中原点为极限点(也可以去掉).
由题意可知,∴.
∴.
∴线段的最大值为.
同课章节目录
