2020-2021学年陕西汉中高一上物理月考试卷Word版含答案
文档属性
| 名称 | 2020-2021学年陕西汉中高一上物理月考试卷Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-09 00:00:00 | ||
图片预览




文档简介
2020-2021学年陕西汉中高一上物理月考试卷
一、选择题
?
1. 在物理学的重大发现中科学家们创造了许多物理学研究方法,如控制变量法、极限思想法、等效替代法、理想模型法、微元法等等,以下叙述中不正确的是(????????)
A.说生活中的下落运动遵循自由落体运动规律采用了理想模型的方法
B.在不需要考虑物体的大小和形状时,用质点来代替实际物体采用了等效替代的方法
C.根据速度定义式v=ΔxΔt,当Δt非常非常小时,ΔxΔt就可以表示物体在t时刻的瞬时速度,该定义采用了极限思维法
D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里采用了微元法
?
2. 由于疫情原因,2020年东京奥运会将延期举行,关于奥运会比赛的论述,下列说法正确的是(????????)
A.运动员铅球成绩为12.50m,指的是铅球被抛出后运动的位移
B.某场球比赛打了加时赛,共需10min,指的是时刻
C.运动员跑完800m比赛,800m指的是路程
D.百米比赛中,一名运动员发现自己在“后退”,他是以大地为参考系
?
3. 甲、乙两物体从同一位置沿同一直线运动的x?t图像(甲的图线为直线,乙的图线为抛物线)如图所示.关于两物体的运动,下列说法正确的是(????????)
A.甲做直线运动,乙做曲线运动
B.0?t1时间内,乙的速度方向与加速度方向相反;t1?t2时间内,乙的速度方向与加速度方向相同
C.0?t2时间内,乙的速度先增大后减小,t2时刻,甲、乙两物体相遇
D.0?t2时间内,t1时刻甲、乙相距最远,两物体一直沿x轴正方向运动
?
4. 物体做匀加速直线运动,相继经过两段距离为16m的路程,第一段用时4s,第二段用时2s,则物体的加速度是(? ? ? ? )
A.23m/s2 B.43m/s2 C.89m/s2 D.169m/s2
?
5. 一个物体从静止开始做匀加速直线运动,以T为时间间隔,在第三个T时间内位移是3m,第三个T时间末的瞬时速度为3m/s,则( )
A.物体的加速度是1m/s2
B.第一个T时间末的瞬时速度为0.6m/s
C.时间间隔T=1s
D.物体在第1个T时间内的位移为0.6m
?
6. 如图所示是一辆摩托车沿直线运动的v?t图像,则摩托车( )
A.速度最大时加速度也最大
B.前10s内的加速度方向保持不变
C.前6s内的位移大于后6s内的位移
D.第4s内运动的方向与第10s内运动的方向相同
?
7. 测速仪安装有超声波发射和接收装置,如图所示,B为测速仪,A为汽车,两者相距335m,某时刻B发出超声波,同时A由静止开始做匀加速直线运动.当B接收到反射回来的超声波信号时,AB相距355m,已知声速为340m/s,则汽车的加速度大小为( )
A.20m/s2 B.10m/s2 C.5m/s2 D.无法确定
?
8. 有一人在平直马路边散步(速度不变),他发现每隔t1时间有一路公共汽车迎面开过,他还发现每隔t2时间有一辆这路公共汽车从身后开过,于是他计算出这路车从汽车站发车的时间间隔是(? ? ? ? )
A.2+t1t2t1+t2 B.2t1t22t1+t2 C.t1t22t1+t2 D.2t1t2t1+t2
?
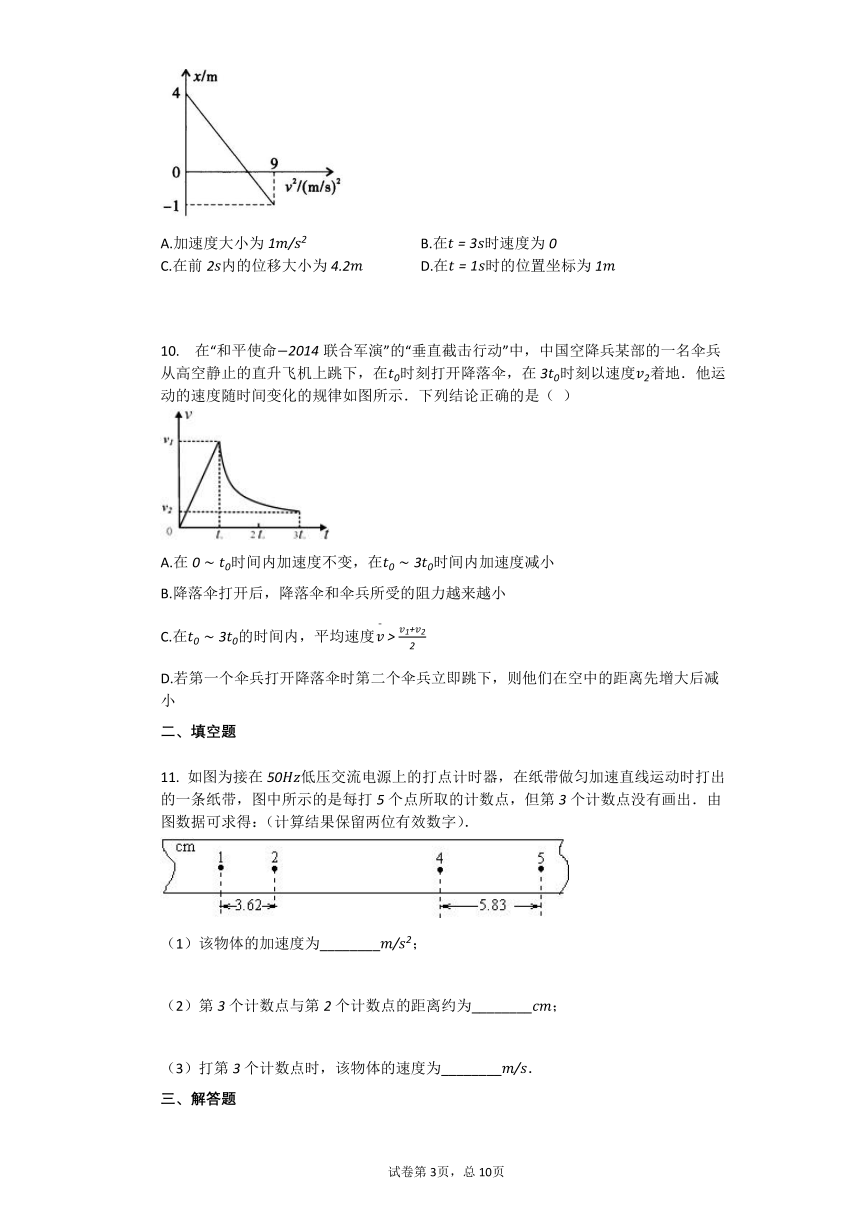
9. 初速度为v0=3m/s的某型号汽车紧急制动时(假设做匀减速直线运动)的x?v2图像如图所示(x为位置坐标,v为汽车的速度),以汽车紧急制动时为计时起点,则该车(????????)
A.加速度大小为1m/s2 B.在t=3s时速度为0
C.在前2s内的位移大小为4.2m D.在t=1s时的位置坐标为1m
?
10. 在“和平使命?2014联合军演”的“垂直截击行动”中,中国空降兵某部的一名伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.他运动的速度随时间变化的规律如图所示.下列结论正确的是( )
A.在0?t0时间内加速度不变,在t0?3t0时间内加速度减小
B.降落伞打开后,降落伞和伞兵所受的阻力越来越小
C.在t0?3t0的时间内,平均速度v?>v1+v22
D.若第一个伞兵打开降落伞时第二个伞兵立即跳下,则他们在空中的距离先增大后减小
二、填空题
?
11. 如图为接在50Hz低压交流电源上的打点计时器,在纸带做匀加速直线运动时打出的一条纸带,图中所示的是每打5个点所取的计数点,但第3个计数点没有画出.由图数据可求得:(计算结果保留两位有效数字).
(1)该物体的加速度为________m/s2;
(2)第3个计数点与第2个计数点的距离约为________cm;
(3)打第3个计数点时,该物体的速度为________m/s.
三、解答题
?
12. 一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站.求:
(1)汽车匀速行驶过程的速度大小?
(2)汽车在刹车过程中的加速度大小?
(3)汽车从甲站到乙站的平均速度?
?
13. 甲乙两个同学在直线跑道上练习4×100m接力,他们奔跑时有相同的最大速度.乙从静止开始全力奔跑需要跑出25m才能达到最大速度,这一过程可看作匀变速运动.现甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑速度达到最大速度的80%,则:
(1)乙在接力区须奔跑出多大距离?
(2)乙应在距离甲多远时起跑?
?
14. 为提高通行效率,许多高速公路出入口安装了电子不停车收费系统ETC.甲、乙两辆汽车分别通过ETC通道和人工收费通道(MTC)驶离高速公路,流程如图所示.假设减速带离收费岛口x=60m,收费岛总长度d=40m,两辆汽车同时以相同的速度v1=72km/h经过减速带后,一起以相同的加速度做匀减速运动.甲车减速至v2=18km/h后,匀速行驶到中心线即可完成缴费,自动栏杆打开放行;乙车刚好到收费岛中心线收费窗口停下,经过t0=20s的时间缴费成功,人工栏打开放行.随后两辆汽车匀加速到速度v1后沿直线匀速行驶,设加速和减速过程中的加速度大小相等,求:
(1)此次人工收费通道和ETC通道打开栏杆放行的时间差;
(2)两辆汽车驶离收费站后相距的最远距离.
参考答案与试题解析
2020-2021学年陕西汉中高一上物理月考试卷
一、选择题
1.
【答案】
B
【考点】
物理学方法
【解答】
解:A.说生活中的下落运动遵循自由落体运动规律时,忽略了空气阻力的作用,故采用了理想模型的方法,故A正确;
B.在不需要考虑物体的大小和形状时,用质点来代替实际物体采用了理想模型的方法,故B错误;
C.根据速度定义式v=ΔxΔt,当Δt非常非常小时,ΔxΔt就可以表示物体在t时刻的瞬时速度,该定义采用了极限思维法,故C正确;
D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加求得位移,这里采用了微元法,故D正确.
本题选择错误的,故选B.
2.
【答案】
C
【考点】
参考系
时间与时刻
位移
路程
【解答】
解:A.运动员铅球成绩为12.50m,指的是水平方向的位移大小为12.50m,故A错误;
B.某场球比赛打了加时赛,共需10min,指的是时间,故B错误;
C.运动员跑完800m比赛,指的是路程大小为800m,故C正确;
D.百米比赛中,一名运动员若以大地为参考系,他是“向前”运动的,故D错误.
故选C.
3.
【答案】
B
【考点】
x-t图像(匀变速直线运动)
【解答】
解:A.由题可知,甲、乙均做直线运动,故A错误;
B.0?t1时间内,乙减速,t1?t2时间内,乙反方向加速,故B正确;
C.0?t2时间内,乙的速度先减小后增大,t2时刻,甲、乙两物体相遇,故C错误;
D.0?t2时间内,t1时刻两图线的差值最大,故在t1时刻,两物体相距最远,但甲物体一直沿x轴负方向运动,乙在0?t1时间内沿x轴负向运动,t1?t2时间内沿x轴正向运动,故D错误.
故选:B.
4.
【答案】
B
【考点】
加速度
【解答】
解:物体做匀加速直线运动,t时间内的平均速度等于t2时刻的瞬时速度,在第一段时间内中间时刻的瞬时速度v1=v?1=164m/s,在第二段时间内中间时刻的瞬时速度v2=v?2=162m/s,两个中间时刻间的时间间隔为总时间的一半,即Δt=3s,则物体的加速度a=v2?v1Δt=8?43m/s2=43m/s2,故B正确.
故选B.
5.
【答案】
D
【考点】
匀变速直线运动规律的综合运用
【解答】
解:AC.根据题意得12a(3T)2?12a(2T)2=3m,v=3aT=3m/s,
联立两式解得a=56m/s2,T=1.2s,故AC错误;
B.第一个T时间末的瞬时速度为v′=aT=1m/s,故B错误;
D.物体在第一个T内的位移x=12aT2=0.6m,故D正确.
故选:D.
6.
【答案】
D
【考点】
v-t图像(匀变速直线运动)
【解答】
解:A.v?t图像的斜率表示加速度,由图中可知,速度最大处的加速度为0,故A错误;
B.斜率的正负表示加速度方向,故在t=6s时,其加速度方向发生变化,故B错误;
C.v?t图像与时间轴围成的面积表示位移,题中可通过格子数粗略估算位移大小,由图中可知前6s的位移小于后6s的位移,故C错误;
D.这里摩托车的速度始终为正值,故其运动方向一直没有发生变化,故D正确.
故选:D.
7.
【答案】
B
【考点】
匀变速直线运动的位移与时间的关系
【解答】
解:设汽车的加速度为a,运动的时间为t,有12at2=355m?335m=20m,
超声波来回的时间为t,则单程的时间为t2,
因为初速度为零的匀加速直线运动,在相等时间内的位移之比为1:3,
在t时间内的位移为20m,则t2时间内的位移为x′=5m,
因此超声波追上汽车时的位移x=5m+335m=340m,
所以t2=xv=1s,则t=2s,所以汽车的加速度大小为10m/s2,故B正确,ACD错误.
故选:B.
8.
【答案】
D
【考点】
匀变速直线运动的速度与时间的关系
【解答】
解:设车速为v车,人的速度为v人,发车时间间隔为t,则有v车?v人t2=v车t,v车+v人t1=v车t,两式联立得t=2t1t2t1+t2,选项D正确.
故选:D.
9.
【答案】
C
【考点】
非常规图象
【解答】
解:A.由v2?v02=2ax可知,图像斜率等于12a,故加速度为a=?0.9m/s2,选项A错误;
B.由Δt=Δva=103s可知,在t=103s时速度为0,选项B错误;
CD.由x=v0t+12at2得2s内位移为4.2m,第1s内的位移为2.55m,在t=1s时的位置坐标为1.45m,故C正确,D错误.
故选:C.
10.
【答案】
A,B,D
【考点】
牛顿运动定律的应用—从运动确定受力
v-t图像(匀变速直线运动)
【解答】
解:A.在0?t0时间伞兵做匀加速直线运动,加速度不变,t0?3t0时间内图线的斜率逐渐减小,则加速度逐渐减小,故A正确.
B.设降落伞和伞兵的总质量为m,所受的阻力为f,加速度大小为a,根据牛顿第二定律得:f?mg=ma,得f=mg+ma,a逐渐减小,则阻力f也逐渐减小,即降落伞和伞兵所受的阻力越来越小,故B正确.
C.在t0?3t0的时间内,假设伞兵做匀减速直线运动,图像为直线,如图中虚线所示,
其平均速度为v1+v22,根据“面积”等于位移可知,匀减速直线运动的位移大于伞兵实际运动的位移,则平均速度v?D.第一个伞兵在空中打开降落伞时的速度比第二个伞兵跳下时速度大,所以两者距离逐渐变大,后来第二个人的速度大于第一个跳伞运动员时,两者距离又减小,即他们在空中的距离先增大后减小,故D正确.
故选:ABD.
二、填空题
11.
【答案】
(1)0.74
(2)4.4
(3)0.47
【考点】
探究小车速度随时间变化的规律
【解答】
解:(1)设1、2间的位移为x1,2、3间的位移为x2,3、4间的位移为x3,4、5间的位移为x4,
因为周期为T′=0.02s,且每打5个点取一个记数点,所以每两个点之间的时间间隔T=0.1s,
由匀变速直线运动的推论xm?xn=(m?n)at2得x4?x1=3at2,
代入数据解得:a=0.74m/s2.
(2)第3个记数点与第2个记数点的距离即为x2,
由匀变速直线运动的推论x2?x1=at2得x2=x1+at2,
代入数据解得:x2=4.4cm.
(3)打第2个点时的瞬时速度等于打1、3之间的平均速度,
因此有:v2=x13t13≈0.40m/s,
根据速度公式v3=v2+at,解得v3≈0.47m/s.
三、解答题
12.
【答案】
(1)汽车匀速行驶过程的速度大小为10m/s.
(2)汽车在刹车过程中的加速度大小为1m/s2.
(3)汽车从甲站到乙站的平均速度为9.44m/s.
【考点】
匀变速直线运动规律的综合运用
平均速度
【解答】
解:(1)汽车匀速行驶过程的速度:v1=a1t1=10m/s.
(2)由v2?v02=2ax知,刹车过程的加速度:a2=v122s3=1m/s2.
(3)加速阶段的位移s1=12at12=25m,
匀速行驶阶段的位移:s2=v1t2=1200m,
减速阶段的时间:t3=v1a2=10s,
所以,全程位移:s=s1+s2+s3=1275m,
全程所用的时间:t=t1+t2+t3=135s,
故汽车从甲站到乙站的平均速度:v?=st≈9.44m/s.
13.
【答案】
(1)乙在接力区须奔跑出的距离为16m;
(2)乙应在距离甲24m时起跑.
【考点】
匀变速直线运动规律的综合运用
【解答】
解:(1)乙起跑后做初速度为0的匀加速直线运动,
设最大速度为v1,达到最大速度经历的位移为x1,乙接棒时的速度为v2,接棒时经历的位移为x2,
所以有:v12=2ax1,
v22=2ax2,
v2=v1×80%,
代入数据解得:x2=0.64x1=16m,
故乙在接力区须奔跑出的距离为16m.
(2)设乙加速至交接棒的时间为t,
该时间内的位移为:x2=0+v22t=0.4v1t=16m,
甲的位移为:x甲=v1t,
两者间的距离为:Δx=x甲?x2=0.6v1t=24m,
故乙应在距离甲24m处起跑.
14.
【答案】
(1)此次人工收费通道和ETC通道打开栏杆放行的时间差为21s;
(2)两辆汽车驶离收费站后相距的最远距离为455m.
【考点】
匀变速直线运动规律的综合运用
【解答】
解:(1)v1=72km/h=20m/s,v2=18km/h=5m/s,
两车减速运动的加速度大小:a=v122(d2+x)=2.5m/s2,
甲车减速到v0,所用时间:t1=v1?v2a=6s,
甲车减速过程走过的距离:x1=v1+v22t1=75m,
甲车从匀速运动到栏杆打开所用时间:t2=(x+d2?x1)v2=1s,
甲车从减速到栏杆打开的总时间:t甲=t1+t2=7s,
乙车减速行驶到收费岛中心线的时间:t3=v1a=8s,
从减速到打开栏杆的总时间:t乙=t0+t3=28s,
人工收收费通道和ETC通道打开栏杆放行的时间差:Δt=t乙?t甲=21s;
(2)乙车从收费岛中心线开始出发又经t3′=8s加速到v1=20m/s,
与甲车达到共同速度,此时两车相距最远,
这个过程乙车行驶的距离与之前乙车减速行驶的距离相等,即x乙=x+d2=80m,
从收费岛中心线开始,甲车先从v2=5m/s加速至v1=20m/s,这个时间为t1′=6s,
然后匀速行驶x甲=x1′+v1(t3′+Δt?t1′)=535m,
故两车相距的最远距离为Δx=x甲?x乙=455m.
一、选择题
?
1. 在物理学的重大发现中科学家们创造了许多物理学研究方法,如控制变量法、极限思想法、等效替代法、理想模型法、微元法等等,以下叙述中不正确的是(????????)
A.说生活中的下落运动遵循自由落体运动规律采用了理想模型的方法
B.在不需要考虑物体的大小和形状时,用质点来代替实际物体采用了等效替代的方法
C.根据速度定义式v=ΔxΔt,当Δt非常非常小时,ΔxΔt就可以表示物体在t时刻的瞬时速度,该定义采用了极限思维法
D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里采用了微元法
?
2. 由于疫情原因,2020年东京奥运会将延期举行,关于奥运会比赛的论述,下列说法正确的是(????????)
A.运动员铅球成绩为12.50m,指的是铅球被抛出后运动的位移
B.某场球比赛打了加时赛,共需10min,指的是时刻
C.运动员跑完800m比赛,800m指的是路程
D.百米比赛中,一名运动员发现自己在“后退”,他是以大地为参考系
?
3. 甲、乙两物体从同一位置沿同一直线运动的x?t图像(甲的图线为直线,乙的图线为抛物线)如图所示.关于两物体的运动,下列说法正确的是(????????)
A.甲做直线运动,乙做曲线运动
B.0?t1时间内,乙的速度方向与加速度方向相反;t1?t2时间内,乙的速度方向与加速度方向相同
C.0?t2时间内,乙的速度先增大后减小,t2时刻,甲、乙两物体相遇
D.0?t2时间内,t1时刻甲、乙相距最远,两物体一直沿x轴正方向运动
?
4. 物体做匀加速直线运动,相继经过两段距离为16m的路程,第一段用时4s,第二段用时2s,则物体的加速度是(? ? ? ? )
A.23m/s2 B.43m/s2 C.89m/s2 D.169m/s2
?
5. 一个物体从静止开始做匀加速直线运动,以T为时间间隔,在第三个T时间内位移是3m,第三个T时间末的瞬时速度为3m/s,则( )
A.物体的加速度是1m/s2
B.第一个T时间末的瞬时速度为0.6m/s
C.时间间隔T=1s
D.物体在第1个T时间内的位移为0.6m
?
6. 如图所示是一辆摩托车沿直线运动的v?t图像,则摩托车( )
A.速度最大时加速度也最大
B.前10s内的加速度方向保持不变
C.前6s内的位移大于后6s内的位移
D.第4s内运动的方向与第10s内运动的方向相同
?
7. 测速仪安装有超声波发射和接收装置,如图所示,B为测速仪,A为汽车,两者相距335m,某时刻B发出超声波,同时A由静止开始做匀加速直线运动.当B接收到反射回来的超声波信号时,AB相距355m,已知声速为340m/s,则汽车的加速度大小为( )
A.20m/s2 B.10m/s2 C.5m/s2 D.无法确定
?
8. 有一人在平直马路边散步(速度不变),他发现每隔t1时间有一路公共汽车迎面开过,他还发现每隔t2时间有一辆这路公共汽车从身后开过,于是他计算出这路车从汽车站发车的时间间隔是(? ? ? ? )
A.2+t1t2t1+t2 B.2t1t22t1+t2 C.t1t22t1+t2 D.2t1t2t1+t2
?
9. 初速度为v0=3m/s的某型号汽车紧急制动时(假设做匀减速直线运动)的x?v2图像如图所示(x为位置坐标,v为汽车的速度),以汽车紧急制动时为计时起点,则该车(????????)
A.加速度大小为1m/s2 B.在t=3s时速度为0
C.在前2s内的位移大小为4.2m D.在t=1s时的位置坐标为1m
?
10. 在“和平使命?2014联合军演”的“垂直截击行动”中,中国空降兵某部的一名伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.他运动的速度随时间变化的规律如图所示.下列结论正确的是( )
A.在0?t0时间内加速度不变,在t0?3t0时间内加速度减小
B.降落伞打开后,降落伞和伞兵所受的阻力越来越小
C.在t0?3t0的时间内,平均速度v?>v1+v22
D.若第一个伞兵打开降落伞时第二个伞兵立即跳下,则他们在空中的距离先增大后减小
二、填空题
?
11. 如图为接在50Hz低压交流电源上的打点计时器,在纸带做匀加速直线运动时打出的一条纸带,图中所示的是每打5个点所取的计数点,但第3个计数点没有画出.由图数据可求得:(计算结果保留两位有效数字).
(1)该物体的加速度为________m/s2;
(2)第3个计数点与第2个计数点的距离约为________cm;
(3)打第3个计数点时,该物体的速度为________m/s.
三、解答题
?
12. 一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站.求:
(1)汽车匀速行驶过程的速度大小?
(2)汽车在刹车过程中的加速度大小?
(3)汽车从甲站到乙站的平均速度?
?
13. 甲乙两个同学在直线跑道上练习4×100m接力,他们奔跑时有相同的最大速度.乙从静止开始全力奔跑需要跑出25m才能达到最大速度,这一过程可看作匀变速运动.现甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑速度达到最大速度的80%,则:
(1)乙在接力区须奔跑出多大距离?
(2)乙应在距离甲多远时起跑?
?
14. 为提高通行效率,许多高速公路出入口安装了电子不停车收费系统ETC.甲、乙两辆汽车分别通过ETC通道和人工收费通道(MTC)驶离高速公路,流程如图所示.假设减速带离收费岛口x=60m,收费岛总长度d=40m,两辆汽车同时以相同的速度v1=72km/h经过减速带后,一起以相同的加速度做匀减速运动.甲车减速至v2=18km/h后,匀速行驶到中心线即可完成缴费,自动栏杆打开放行;乙车刚好到收费岛中心线收费窗口停下,经过t0=20s的时间缴费成功,人工栏打开放行.随后两辆汽车匀加速到速度v1后沿直线匀速行驶,设加速和减速过程中的加速度大小相等,求:
(1)此次人工收费通道和ETC通道打开栏杆放行的时间差;
(2)两辆汽车驶离收费站后相距的最远距离.
参考答案与试题解析
2020-2021学年陕西汉中高一上物理月考试卷
一、选择题
1.
【答案】
B
【考点】
物理学方法
【解答】
解:A.说生活中的下落运动遵循自由落体运动规律时,忽略了空气阻力的作用,故采用了理想模型的方法,故A正确;
B.在不需要考虑物体的大小和形状时,用质点来代替实际物体采用了理想模型的方法,故B错误;
C.根据速度定义式v=ΔxΔt,当Δt非常非常小时,ΔxΔt就可以表示物体在t时刻的瞬时速度,该定义采用了极限思维法,故C正确;
D.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加求得位移,这里采用了微元法,故D正确.
本题选择错误的,故选B.
2.
【答案】
C
【考点】
参考系
时间与时刻
位移
路程
【解答】
解:A.运动员铅球成绩为12.50m,指的是水平方向的位移大小为12.50m,故A错误;
B.某场球比赛打了加时赛,共需10min,指的是时间,故B错误;
C.运动员跑完800m比赛,指的是路程大小为800m,故C正确;
D.百米比赛中,一名运动员若以大地为参考系,他是“向前”运动的,故D错误.
故选C.
3.
【答案】
B
【考点】
x-t图像(匀变速直线运动)
【解答】
解:A.由题可知,甲、乙均做直线运动,故A错误;
B.0?t1时间内,乙减速,t1?t2时间内,乙反方向加速,故B正确;
C.0?t2时间内,乙的速度先减小后增大,t2时刻,甲、乙两物体相遇,故C错误;
D.0?t2时间内,t1时刻两图线的差值最大,故在t1时刻,两物体相距最远,但甲物体一直沿x轴负方向运动,乙在0?t1时间内沿x轴负向运动,t1?t2时间内沿x轴正向运动,故D错误.
故选:B.
4.
【答案】
B
【考点】
加速度
【解答】
解:物体做匀加速直线运动,t时间内的平均速度等于t2时刻的瞬时速度,在第一段时间内中间时刻的瞬时速度v1=v?1=164m/s,在第二段时间内中间时刻的瞬时速度v2=v?2=162m/s,两个中间时刻间的时间间隔为总时间的一半,即Δt=3s,则物体的加速度a=v2?v1Δt=8?43m/s2=43m/s2,故B正确.
故选B.
5.
【答案】
D
【考点】
匀变速直线运动规律的综合运用
【解答】
解:AC.根据题意得12a(3T)2?12a(2T)2=3m,v=3aT=3m/s,
联立两式解得a=56m/s2,T=1.2s,故AC错误;
B.第一个T时间末的瞬时速度为v′=aT=1m/s,故B错误;
D.物体在第一个T内的位移x=12aT2=0.6m,故D正确.
故选:D.
6.
【答案】
D
【考点】
v-t图像(匀变速直线运动)
【解答】
解:A.v?t图像的斜率表示加速度,由图中可知,速度最大处的加速度为0,故A错误;
B.斜率的正负表示加速度方向,故在t=6s时,其加速度方向发生变化,故B错误;
C.v?t图像与时间轴围成的面积表示位移,题中可通过格子数粗略估算位移大小,由图中可知前6s的位移小于后6s的位移,故C错误;
D.这里摩托车的速度始终为正值,故其运动方向一直没有发生变化,故D正确.
故选:D.
7.
【答案】
B
【考点】
匀变速直线运动的位移与时间的关系
【解答】
解:设汽车的加速度为a,运动的时间为t,有12at2=355m?335m=20m,
超声波来回的时间为t,则单程的时间为t2,
因为初速度为零的匀加速直线运动,在相等时间内的位移之比为1:3,
在t时间内的位移为20m,则t2时间内的位移为x′=5m,
因此超声波追上汽车时的位移x=5m+335m=340m,
所以t2=xv=1s,则t=2s,所以汽车的加速度大小为10m/s2,故B正确,ACD错误.
故选:B.
8.
【答案】
D
【考点】
匀变速直线运动的速度与时间的关系
【解答】
解:设车速为v车,人的速度为v人,发车时间间隔为t,则有v车?v人t2=v车t,v车+v人t1=v车t,两式联立得t=2t1t2t1+t2,选项D正确.
故选:D.
9.
【答案】
C
【考点】
非常规图象
【解答】
解:A.由v2?v02=2ax可知,图像斜率等于12a,故加速度为a=?0.9m/s2,选项A错误;
B.由Δt=Δva=103s可知,在t=103s时速度为0,选项B错误;
CD.由x=v0t+12at2得2s内位移为4.2m,第1s内的位移为2.55m,在t=1s时的位置坐标为1.45m,故C正确,D错误.
故选:C.
10.
【答案】
A,B,D
【考点】
牛顿运动定律的应用—从运动确定受力
v-t图像(匀变速直线运动)
【解答】
解:A.在0?t0时间伞兵做匀加速直线运动,加速度不变,t0?3t0时间内图线的斜率逐渐减小,则加速度逐渐减小,故A正确.
B.设降落伞和伞兵的总质量为m,所受的阻力为f,加速度大小为a,根据牛顿第二定律得:f?mg=ma,得f=mg+ma,a逐渐减小,则阻力f也逐渐减小,即降落伞和伞兵所受的阻力越来越小,故B正确.
C.在t0?3t0的时间内,假设伞兵做匀减速直线运动,图像为直线,如图中虚线所示,
其平均速度为v1+v22,根据“面积”等于位移可知,匀减速直线运动的位移大于伞兵实际运动的位移,则平均速度v?
故选:ABD.
二、填空题
11.
【答案】
(1)0.74
(2)4.4
(3)0.47
【考点】
探究小车速度随时间变化的规律
【解答】
解:(1)设1、2间的位移为x1,2、3间的位移为x2,3、4间的位移为x3,4、5间的位移为x4,
因为周期为T′=0.02s,且每打5个点取一个记数点,所以每两个点之间的时间间隔T=0.1s,
由匀变速直线运动的推论xm?xn=(m?n)at2得x4?x1=3at2,
代入数据解得:a=0.74m/s2.
(2)第3个记数点与第2个记数点的距离即为x2,
由匀变速直线运动的推论x2?x1=at2得x2=x1+at2,
代入数据解得:x2=4.4cm.
(3)打第2个点时的瞬时速度等于打1、3之间的平均速度,
因此有:v2=x13t13≈0.40m/s,
根据速度公式v3=v2+at,解得v3≈0.47m/s.
三、解答题
12.
【答案】
(1)汽车匀速行驶过程的速度大小为10m/s.
(2)汽车在刹车过程中的加速度大小为1m/s2.
(3)汽车从甲站到乙站的平均速度为9.44m/s.
【考点】
匀变速直线运动规律的综合运用
平均速度
【解答】
解:(1)汽车匀速行驶过程的速度:v1=a1t1=10m/s.
(2)由v2?v02=2ax知,刹车过程的加速度:a2=v122s3=1m/s2.
(3)加速阶段的位移s1=12at12=25m,
匀速行驶阶段的位移:s2=v1t2=1200m,
减速阶段的时间:t3=v1a2=10s,
所以,全程位移:s=s1+s2+s3=1275m,
全程所用的时间:t=t1+t2+t3=135s,
故汽车从甲站到乙站的平均速度:v?=st≈9.44m/s.
13.
【答案】
(1)乙在接力区须奔跑出的距离为16m;
(2)乙应在距离甲24m时起跑.
【考点】
匀变速直线运动规律的综合运用
【解答】
解:(1)乙起跑后做初速度为0的匀加速直线运动,
设最大速度为v1,达到最大速度经历的位移为x1,乙接棒时的速度为v2,接棒时经历的位移为x2,
所以有:v12=2ax1,
v22=2ax2,
v2=v1×80%,
代入数据解得:x2=0.64x1=16m,
故乙在接力区须奔跑出的距离为16m.
(2)设乙加速至交接棒的时间为t,
该时间内的位移为:x2=0+v22t=0.4v1t=16m,
甲的位移为:x甲=v1t,
两者间的距离为:Δx=x甲?x2=0.6v1t=24m,
故乙应在距离甲24m处起跑.
14.
【答案】
(1)此次人工收费通道和ETC通道打开栏杆放行的时间差为21s;
(2)两辆汽车驶离收费站后相距的最远距离为455m.
【考点】
匀变速直线运动规律的综合运用
【解答】
解:(1)v1=72km/h=20m/s,v2=18km/h=5m/s,
两车减速运动的加速度大小:a=v122(d2+x)=2.5m/s2,
甲车减速到v0,所用时间:t1=v1?v2a=6s,
甲车减速过程走过的距离:x1=v1+v22t1=75m,
甲车从匀速运动到栏杆打开所用时间:t2=(x+d2?x1)v2=1s,
甲车从减速到栏杆打开的总时间:t甲=t1+t2=7s,
乙车减速行驶到收费岛中心线的时间:t3=v1a=8s,
从减速到打开栏杆的总时间:t乙=t0+t3=28s,
人工收收费通道和ETC通道打开栏杆放行的时间差:Δt=t乙?t甲=21s;
(2)乙车从收费岛中心线开始出发又经t3′=8s加速到v1=20m/s,
与甲车达到共同速度,此时两车相距最远,
这个过程乙车行驶的距离与之前乙车减速行驶的距离相等,即x乙=x+d2=80m,
从收费岛中心线开始,甲车先从v2=5m/s加速至v1=20m/s,这个时间为t1′=6s,
然后匀速行驶x甲=x1′+v1(t3′+Δt?t1′)=535m,
故两车相距的最远距离为Δx=x甲?x乙=455m.
同课章节目录
