第三章 函数的应用 章末检测(含解析)
文档属性
| 名称 | 第三章 函数的应用 章末检测(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
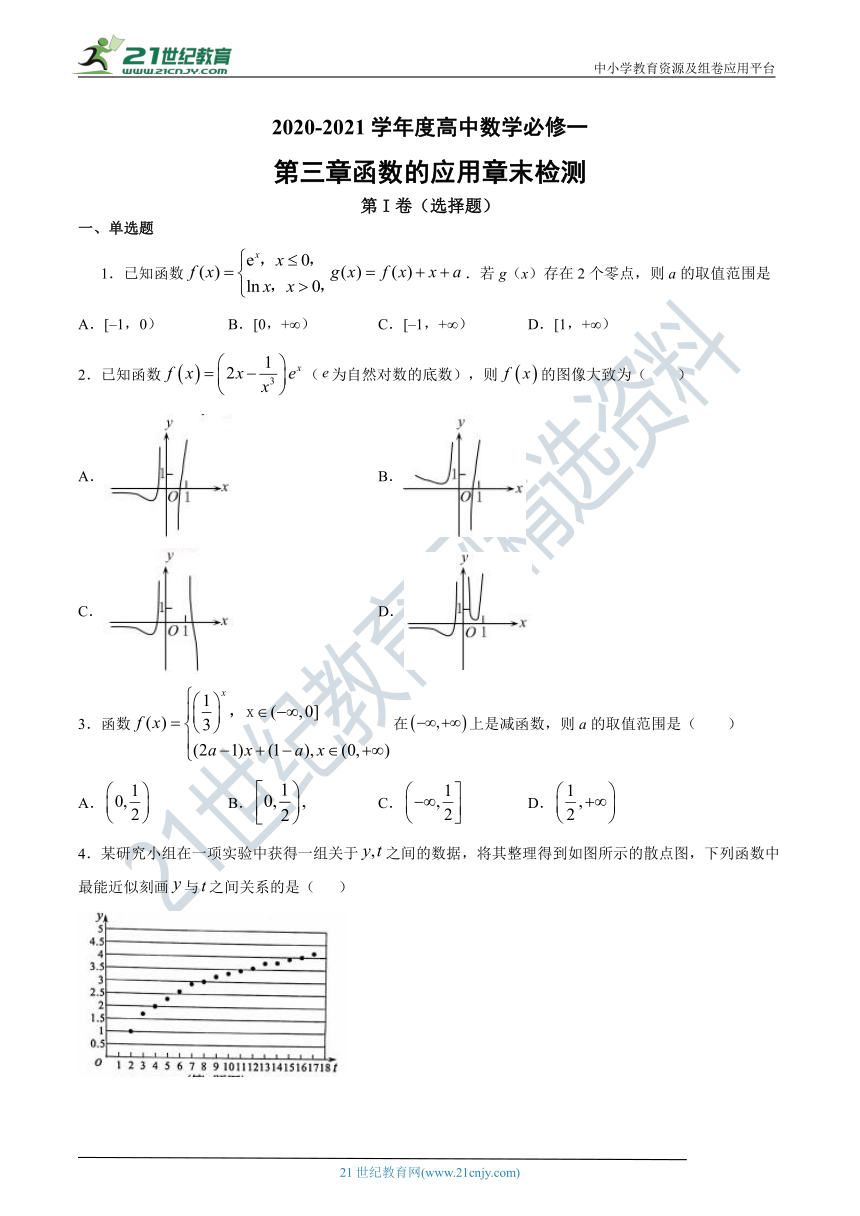
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年度高中数学必修一
第三章函数的应用章末检测
第I卷(选择题)
一、单选题
1.已知函数.若g(x)存在2个零点,则a的取值范围是
A.[–1,0)
B.[0,+∞)
C.[–1,+∞)
D.[1,+∞)
2.已知函数(为自然对数的底数),则的图像大致为(
)
A.
B.
C.
D.
3.函数在上是减函数,则a的取值范围是(
)
A.
B.
C.
D.
4.某研究小组在一项实验中获得一组关于之间的数据,将其整理得到如图所示的散点图,下列函数中最能近似刻画与之间关系的是(
)
A.
B.
C.
D.
5.已知是函数的一个零点,若,则(
)
A.,
B.,
C.,
D.,
6.在下列区间中,函数的零点所在的区间为(
)
A.
B.
C.
D.
7.函数的零点个数为
(
)
A.0
B.1
C.2
D.3
8.下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )
A.
B.
C.
D.
9.已知函数,若函数y=f(x)–m有三个不同的零点,则实数m的取值范围是(
)
A.[1,2]
B.[1,2)
C.(1,2]
D.(1,2)
10.2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数
1~50
51~100
100以上
门票价格
13元/人
11元/人
9元/人
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为(
)
A.20
B.30
C.35
D.40
11.若函数
(a∈R)在区间(1,2)上有零点,则a的值可能是( )
A.-2
B.0
C.1
D.3
12.如果已知0A.2
B.3
C.4
D.与a的值有关
第II卷(非选择题)
二、解答题
13.已知是定义域为的奇函数,当时,.
(1)写出函数的解析式;
(2)若方程恰3有个不同的解,求的取值范围.
14.已知二次函数满足,且,.
(1)求的解析式;
(2)是否存在实数,使得在上的图象恒在曲线的上方?若存在,求出的取值范围;若不存在,说明理由.
15.某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:
x
30
40
45
50
y
60
30
15
0
(1)在所给的坐标图纸中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?
16.如图,建立平面直角坐标系,轴在地平面上,轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上,其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标不超过多少时,炮弹可以击中它?请说明理由.
17.某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x吨、3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
18.已知函数,.
(1)若在区间上单调递增,求m的取值范围;
(2)求在区间上的最小值;
(3)讨论在区间上的零点个数.
三、填空题
19.已知函数f(x)=logax+x-b(a>0,且a≠1).当2<a<3<b<4时,函数f(x)的零点为x0∈(n,n+1),n∈N
,则n=
.
20.若函数对于时,恒有,则实数的取值范围是_____.
21.已知函数.若函数有两个零点,则实数的取值范围是_____.
22.若只有一个实数解,则实数的取值范围_____.
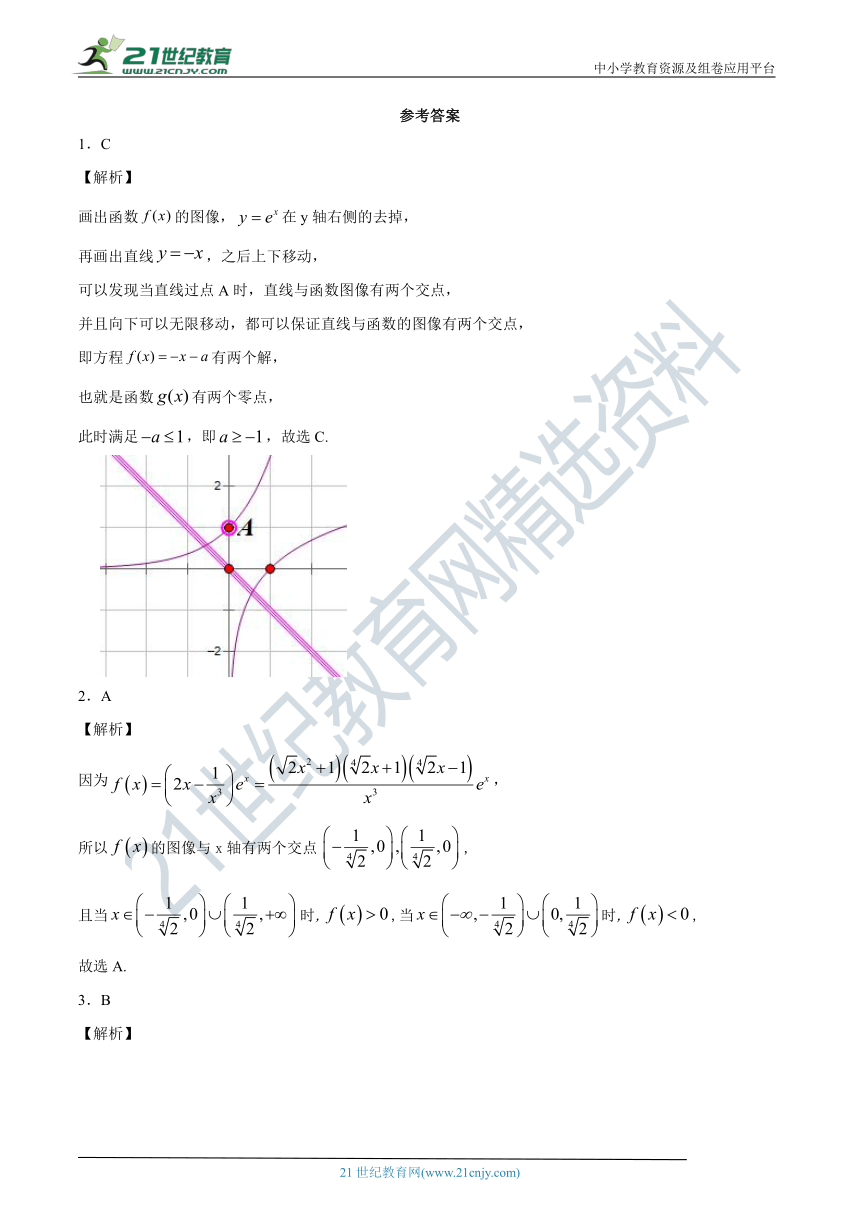
参考答案
1.C
【解析】
画出函数的图像,在y轴右侧的去掉,
再画出直线,之后上下移动,
可以发现当直线过点A时,直线与函数图像有两个交点,
并且向下可以无限移动,都可以保证直线与函数的图像有两个交点,
即方程有两个解,
也就是函数有两个零点,
此时满足,即,故选C.
2.A
【解析】
因为,
所以的图像与x轴有两个交点,
且当时,,当时,,
故选A.
3.B
【解析】
解:依题意,,解得,
故选B.
4.C
【解析】
根据图中的特殊点(2,1),(4,2),通过选项可知只有C:满足题意.故选C.
5.B
【解析】
因为是函数的一个零点,则是函数与的交点的横坐标,画出函数图像,如图所示,
则当时,在下方,即;
当时,在上方,即,
故选:B
6.C
【解析】
因为函数在上连续单调递增,
且,
所以函数的零点在区间内,故选C.
7.B
8.C
【解析】
解:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)?f(b)<0A、B中不存在f(x)<0,D中函数不连续.
故选C.
9.D
【解析】
画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)–m有三个不同的零点,∴函数y=f(x)与y=m的图象有3个交点,由图象可得m的取值范围为(1,2).
故选:D.
10.B
【解析】
由题意,990不能被13整除,所以两个部门的人数之和为,
(1)若,则,可得,……(1)
由共需支付门票为1290元,可知,………(2)
联立方程组,可得(舍去);
(2)若,则,可得,……(3)
由共需支付门票为1290元,可知,可得,…(4)
联立方程组可得,
所以两个部门的人数之差为.
故选:B.
11.A
【解析】
函数的图象在上是连续不断的,逐个选项代入验证,当时,,.故在区间上有零点,同理,其他选项不符合,
故选A.
12.A
【解析】
设分别作出它们的图象如图所示:
由图可知有两个交点,故选A.
13.(1)
(2)
【解析】
解:(1)当时,,
是奇函数,
.
(2)当时,,最小值为;
当,,最大值为.
据此可作出函数的图象,如图所示,
根据图象得,若方程恰有个不同的解,
则的取值范围是.
14.(1)
(2)
【解析】
(1)设,
因为二次函数满足,所以的图象关于直线对称,
即①
因为,,所以
②
,③
联立①②③,解得,,.
故.
(2)设,
的图象恒在曲线的上方等价于恒成立,
即恒成立,
因为在上单调递减,在上单调递增,
所以在上单调递减,
则.
故的取值范围为.
15.(1)y=-3x+150(0≤x≤50且x∈N
).
(2)销售单价为40元时,才能获得最大日销售利润.
【解析】
试题分析:(1)由题意画出所给的点,结合题意求解一次函数的解析式即可;
(2)结合(1)的结论和二次函数的性质整理计算即可求得最终结果.
试题解析:
(1)由表作出点(30,60),(40,30),(45,15),(50,0).如图,它们近似地在一条直线上,设它们共线于直线y=kx+b,
∴解得
∴y=-3x+150,(x∈N).
经检验(30,60),(40,30)也在此直线上.
∴所求函数解析式为y=-3x+150,(x∈N).
(2)依题意P=y(x-30)=(-3x+150)(x-30)=-3(x-40)2+300,
当x=40时,P有最大值300,故销售价为40元时,才能获得最大利润.
16.(1)炮的最大射程是10千米.
(2)当不超过6千米时,炮弹可以击中目标.
【解析】
(1)令y=0,得kx-
(1+k2)x2=0,
由实际意义和题设条件知x>0,k>0,
故x==≤=10,当且仅当k=1时取等号.所以炮的最大射程为10千米.
(2)因为a>0,所以炮弹可击中目标
?存在k>0,使3.2=ka-
(1+k2)a2成立
?关于k的方程a2k2-20ak+a2+64=0有正根
?判别式Δ=(-20a)2-4a2(a2+64)≥0
?a≤6.
所以当a不超过6(千米)时,可击中目标.
17.(1)
(2)甲户用水量为5x=7.5吨,
付费S1=4×1.8+3.5×3=17.70(元);
乙户用水量为3x=4.5吨,
付费S2=4×1.8+0.5×3=8.70(元).
【解析】
(1)当,即时,,所以.-------1分
当,,
即,.------3分
当,即时,
,------4分
综上:-------5分
(2)由(1)知:当时,;当时,;当时,.所以若甲、乙两户共交水费26.4元时,------7分
所以,解得:;-------9分
所以甲户用水量为7.5吨,应缴水费元;乙户用水量为4.5吨,应缴水费元.-------10分
18.(1);(2);(3)当时,函数有2个零点,当或时,函数有1个零点.
【解析】
(1)由题意,函数开口向上,对称轴的方程为,
若使得函数在上单调递增,则满足,解得,
即实数m的取值范围.
(2)①当即时,函数在区间单调递增,
所以函数的最小值为;
②当,即时,
函数在区间单调递减,在区间上单调递增,
所以函数的最小值为;
③当即时,函数在区间单调递减,
所以函数的最小值为,
综上可得,函数的最小值为.
(3)因为函数的对称轴方程为,且恒成立,
①当,即时,函数在区间上有2个零点;
②当,此时m不存在;
③当,此时m不存在;
④当,即,解得或时,函数在区间上有1个零点.
综上可得:当时,函数在区间上有2个零点,
当或时,函数在区间上有1个零点.
19.2
【解析】
设函数y=logax,m=﹣x+b
根据2<a<3<b<4,
对于函数y=logax
在x=2时,一定得到一个值小于1,而b-2>1,x=3时,对数值在1和2
之间,b-3<1
在同一坐标系中画出两个函数的图象,
判断两个函数的图形的交点在(2,3)之间,
∴函数f(x)的零点x0∈(n,n+1)时,n=2.故答案为2.
20.
【解析】
函数对于时,恒有,
等价于恒成立,当x=1时,不等式恒成立,a的取值是全体实数;
当时,不等式等价于,根据反比例函数的性质得到,故得到.两种情况对a的范围取交集即可.
故答案为.
21.
【解析】
函数有两个零点即与有两个交点,
的图像如图所示:当的斜率时由图像可得有两个交点,故实数的取值范围是
故答案为
22.或
【解析】
作出函数的图象,如图所示,
结合图象可得,方程只有一个实数解,
即函数与的图象只有一个交点,
则满足或.
故答案为:或.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
2020-2021学年度高中数学必修一
第三章函数的应用章末检测
第I卷(选择题)
一、单选题
1.已知函数.若g(x)存在2个零点,则a的取值范围是
A.[–1,0)
B.[0,+∞)
C.[–1,+∞)
D.[1,+∞)
2.已知函数(为自然对数的底数),则的图像大致为(
)
A.
B.
C.
D.
3.函数在上是减函数,则a的取值范围是(
)
A.
B.
C.
D.
4.某研究小组在一项实验中获得一组关于之间的数据,将其整理得到如图所示的散点图,下列函数中最能近似刻画与之间关系的是(
)
A.
B.
C.
D.
5.已知是函数的一个零点,若,则(
)
A.,
B.,
C.,
D.,
6.在下列区间中,函数的零点所在的区间为(
)
A.
B.
C.
D.
7.函数的零点个数为
(
)
A.0
B.1
C.2
D.3
8.下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )
A.
B.
C.
D.
9.已知函数,若函数y=f(x)–m有三个不同的零点,则实数m的取值范围是(
)
A.[1,2]
B.[1,2)
C.(1,2]
D.(1,2)
10.2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数
1~50
51~100
100以上
门票价格
13元/人
11元/人
9元/人
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为(
)
A.20
B.30
C.35
D.40
11.若函数
(a∈R)在区间(1,2)上有零点,则a的值可能是( )
A.-2
B.0
C.1
D.3
12.如果已知0
B.3
C.4
D.与a的值有关
第II卷(非选择题)
二、解答题
13.已知是定义域为的奇函数,当时,.
(1)写出函数的解析式;
(2)若方程恰3有个不同的解,求的取值范围.
14.已知二次函数满足,且,.
(1)求的解析式;
(2)是否存在实数,使得在上的图象恒在曲线的上方?若存在,求出的取值范围;若不存在,说明理由.
15.某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:
x
30
40
45
50
y
60
30
15
0
(1)在所给的坐标图纸中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?
16.如图,建立平面直角坐标系,轴在地平面上,轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上,其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标不超过多少时,炮弹可以击中它?请说明理由.
17.某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x吨、3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
18.已知函数,.
(1)若在区间上单调递增,求m的取值范围;
(2)求在区间上的最小值;
(3)讨论在区间上的零点个数.
三、填空题
19.已知函数f(x)=logax+x-b(a>0,且a≠1).当2<a<3<b<4时,函数f(x)的零点为x0∈(n,n+1),n∈N
,则n=
.
20.若函数对于时,恒有,则实数的取值范围是_____.
21.已知函数.若函数有两个零点,则实数的取值范围是_____.
22.若只有一个实数解,则实数的取值范围_____.
参考答案
1.C
【解析】
画出函数的图像,在y轴右侧的去掉,
再画出直线,之后上下移动,
可以发现当直线过点A时,直线与函数图像有两个交点,
并且向下可以无限移动,都可以保证直线与函数的图像有两个交点,
即方程有两个解,
也就是函数有两个零点,
此时满足,即,故选C.
2.A
【解析】
因为,
所以的图像与x轴有两个交点,
且当时,,当时,,
故选A.
3.B
【解析】
解:依题意,,解得,
故选B.
4.C
【解析】
根据图中的特殊点(2,1),(4,2),通过选项可知只有C:满足题意.故选C.
5.B
【解析】
因为是函数的一个零点,则是函数与的交点的横坐标,画出函数图像,如图所示,
则当时,在下方,即;
当时,在上方,即,
故选:B
6.C
【解析】
因为函数在上连续单调递增,
且,
所以函数的零点在区间内,故选C.
7.B
8.C
【解析】
解:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)?f(b)<0A、B中不存在f(x)<0,D中函数不连续.
故选C.
9.D
【解析】
画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)–m有三个不同的零点,∴函数y=f(x)与y=m的图象有3个交点,由图象可得m的取值范围为(1,2).
故选:D.
10.B
【解析】
由题意,990不能被13整除,所以两个部门的人数之和为,
(1)若,则,可得,……(1)
由共需支付门票为1290元,可知,………(2)
联立方程组,可得(舍去);
(2)若,则,可得,……(3)
由共需支付门票为1290元,可知,可得,…(4)
联立方程组可得,
所以两个部门的人数之差为.
故选:B.
11.A
【解析】
函数的图象在上是连续不断的,逐个选项代入验证,当时,,.故在区间上有零点,同理,其他选项不符合,
故选A.
12.A
【解析】
设分别作出它们的图象如图所示:
由图可知有两个交点,故选A.
13.(1)
(2)
【解析】
解:(1)当时,,
是奇函数,
.
(2)当时,,最小值为;
当,,最大值为.
据此可作出函数的图象,如图所示,
根据图象得,若方程恰有个不同的解,
则的取值范围是.
14.(1)
(2)
【解析】
(1)设,
因为二次函数满足,所以的图象关于直线对称,
即①
因为,,所以
②
,③
联立①②③,解得,,.
故.
(2)设,
的图象恒在曲线的上方等价于恒成立,
即恒成立,
因为在上单调递减,在上单调递增,
所以在上单调递减,
则.
故的取值范围为.
15.(1)y=-3x+150(0≤x≤50且x∈N
).
(2)销售单价为40元时,才能获得最大日销售利润.
【解析】
试题分析:(1)由题意画出所给的点,结合题意求解一次函数的解析式即可;
(2)结合(1)的结论和二次函数的性质整理计算即可求得最终结果.
试题解析:
(1)由表作出点(30,60),(40,30),(45,15),(50,0).如图,它们近似地在一条直线上,设它们共线于直线y=kx+b,
∴解得
∴y=-3x+150,(x∈N).
经检验(30,60),(40,30)也在此直线上.
∴所求函数解析式为y=-3x+150,(x∈N).
(2)依题意P=y(x-30)=(-3x+150)(x-30)=-3(x-40)2+300,
当x=40时,P有最大值300,故销售价为40元时,才能获得最大利润.
16.(1)炮的最大射程是10千米.
(2)当不超过6千米时,炮弹可以击中目标.
【解析】
(1)令y=0,得kx-
(1+k2)x2=0,
由实际意义和题设条件知x>0,k>0,
故x==≤=10,当且仅当k=1时取等号.所以炮的最大射程为10千米.
(2)因为a>0,所以炮弹可击中目标
?存在k>0,使3.2=ka-
(1+k2)a2成立
?关于k的方程a2k2-20ak+a2+64=0有正根
?判别式Δ=(-20a)2-4a2(a2+64)≥0
?a≤6.
所以当a不超过6(千米)时,可击中目标.
17.(1)
(2)甲户用水量为5x=7.5吨,
付费S1=4×1.8+3.5×3=17.70(元);
乙户用水量为3x=4.5吨,
付费S2=4×1.8+0.5×3=8.70(元).
【解析】
(1)当,即时,,所以.-------1分
当,,
即,.------3分
当,即时,
,------4分
综上:-------5分
(2)由(1)知:当时,;当时,;当时,.所以若甲、乙两户共交水费26.4元时,------7分
所以,解得:;-------9分
所以甲户用水量为7.5吨,应缴水费元;乙户用水量为4.5吨,应缴水费元.-------10分
18.(1);(2);(3)当时,函数有2个零点,当或时,函数有1个零点.
【解析】
(1)由题意,函数开口向上,对称轴的方程为,
若使得函数在上单调递增,则满足,解得,
即实数m的取值范围.
(2)①当即时,函数在区间单调递增,
所以函数的最小值为;
②当,即时,
函数在区间单调递减,在区间上单调递增,
所以函数的最小值为;
③当即时,函数在区间单调递减,
所以函数的最小值为,
综上可得,函数的最小值为.
(3)因为函数的对称轴方程为,且恒成立,
①当,即时,函数在区间上有2个零点;
②当,此时m不存在;
③当,此时m不存在;
④当,即,解得或时,函数在区间上有1个零点.
综上可得:当时,函数在区间上有2个零点,
当或时,函数在区间上有1个零点.
19.2
【解析】
设函数y=logax,m=﹣x+b
根据2<a<3<b<4,
对于函数y=logax
在x=2时,一定得到一个值小于1,而b-2>1,x=3时,对数值在1和2
之间,b-3<1
在同一坐标系中画出两个函数的图象,
判断两个函数的图形的交点在(2,3)之间,
∴函数f(x)的零点x0∈(n,n+1)时,n=2.故答案为2.
20.
【解析】
函数对于时,恒有,
等价于恒成立,当x=1时,不等式恒成立,a的取值是全体实数;
当时,不等式等价于,根据反比例函数的性质得到,故得到.两种情况对a的范围取交集即可.
故答案为.
21.
【解析】
函数有两个零点即与有两个交点,
的图像如图所示:当的斜率时由图像可得有两个交点,故实数的取值范围是
故答案为
22.或
【解析】
作出函数的图象,如图所示,
结合图象可得,方程只有一个实数解,
即函数与的图象只有一个交点,
则满足或.
故答案为:或.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
