人教新课标数学五年级上册《用计算器探索规律 1》ppt课件
文档属性
| 名称 | 人教新课标数学五年级上册《用计算器探索规律 1》ppt课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 884.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-25 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
人教新课标五年级数学上册
教学目标
1.知识目标:能借助计算器探求简单的数学规律。
2.能力目标:培养观察、归纳、概括、推理的数学能力。
3.情感目标:感受信息化时代,计算器(或计算机)是探索数学知识的有力工具。
400÷75=______(米)
平均每秒跑多少米呢?
哇!王鹏400米只跑了75秒!
400÷75=______(米)
5
)
4 0 0
75
3 7 5
2 5
3
2 2 5
2 5
.
观察这个竖式,你发现了什么?
余数怎么总是“25”?
商的小数部分总是重复出现“3”。
继续除下去,可能永远也除不完。
0
0
3
2 2 5
2 5
0
3
2 2 5
2 5
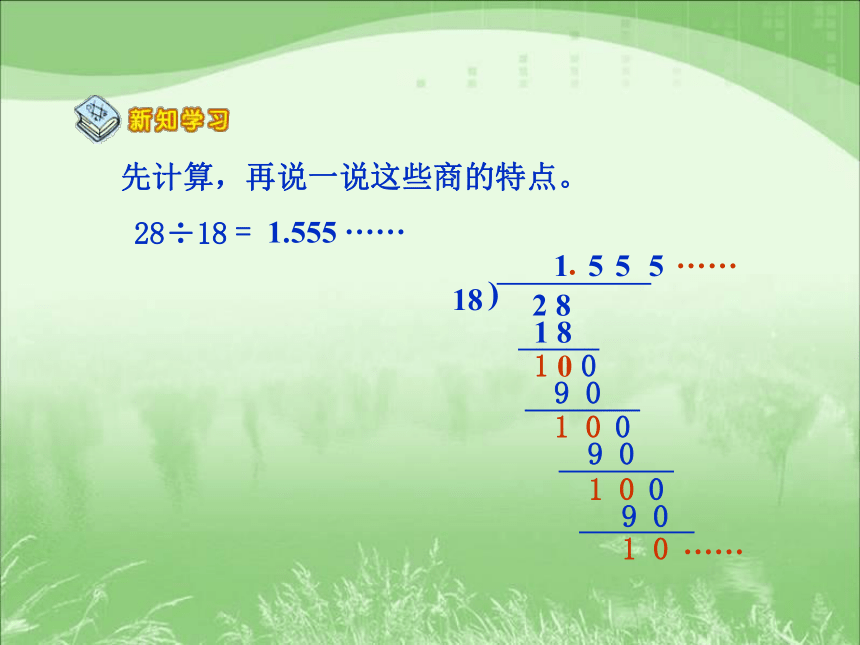
先计算,再说一说这些商的特点。
)
2 8
18
1
.
5
1 8
1 0
0
9 0
1 0
28÷18
0
5
9 0
1 0
0
5
9 0
1 0
……
……
= 1.555
……
)
7 8 . 6
11
7
.
1
7 7
1
6
1 1
5
78.6÷11
0
4
4 4
6
0
5
5 5
5
……
= 7.14545
……
0
4
4 4
6
0
5
5 5
5
……
5.333…和7.14545…都是循环小数。
一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫循环小数。
5.333…还可以写作5.3,
7.14545…还可以写作7.145。
.
.
.
想一想
两个数相除,如果不能得到整数商,所得的商会有哪些情况?
15÷16 = 。 1.5÷7 = 。
0.9375
小数部分的位数是有限的小数,叫做有限小数。
例如,0.9375是一个有限小数。
小数部分的位数是无限的小数,叫做无限小数。
例如,0.2142857142857…就是一个无限小数。
0.2142857142857…
依次不断重复出现的数字是?
3.4666 ( )
0.24382438 ( )
8.4747 ( )
0.44222 ( )
……
……
……
……
6
2438
47
2
一个循环小数的小数部分,依次不断重复出现的数字,叫做这个循环小数的循环节。例如,5.33…的循环节是3,7.14545…的循环节是45。写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位上面各记一个圆点。例如,
5.33…写作5.3,7.14545…写作7.145。
.
.
.
循环节
1÷11= 0.0909…
2÷11= 0.1818…
3÷11=______
4÷11=______
5÷11=______
用计算器计算下面各题目。
0.2727…
0.3636…
0.4545…
它们的商都是循环小数。
你发现了什么规律?
不计算,用发现的规律直接写出下面几道题的商。
6÷11=______
7÷11=______
8÷11=______
9÷11=_____
0.5454…
0.6363…
0.7272…
0.8181…
用计算器计算前4题,试着写出后2题的积。
3×7 = 。
3.3×6.7 = 。
3.33×66.7 = 。
3.333×666.7 = 。
3.3333×6666.7 = 。
3.33333×66666.7 = 。
21
22.11
222.111
2222.1111
22222.11111
222222.111111
不计算,运用规律直接填出得数。
6×7 = 42
6.6×6.7 = 44.22
6.66×66.7 = 。
6.666×666.7 = 。
444.222
4444.2222
先找规律,再按规律填数。
(1)6.25 2.5 1 0.064
(2)7 3.5 1.75 0.21875
0.4 0.16
0.875 0.4375
数字黑洞是指自然数经过某种数学运算之后陷入了一种循环的情况。例如,任意四个不同的数字,组成一个最大的数和一个最小的数,用大数减去小数。用所得结果的四位数重复上述过程,最多七步,必得6174。即:7614-1467=6174。仿佛掉进了黑洞,永远出不来。不信的话,请你试一试!
什么是“数字黑洞”?
本课小结
本课关键不在于如何使用计算器,而是要我们通过观察找出商的规律,把得出的规律应用于后续的计算。
人教新课标五年级数学上册
教学目标
1.知识目标:能借助计算器探求简单的数学规律。
2.能力目标:培养观察、归纳、概括、推理的数学能力。
3.情感目标:感受信息化时代,计算器(或计算机)是探索数学知识的有力工具。
400÷75=______(米)
平均每秒跑多少米呢?
哇!王鹏400米只跑了75秒!
400÷75=______(米)
5
)
4 0 0
75
3 7 5
2 5
3
2 2 5
2 5
.
观察这个竖式,你发现了什么?
余数怎么总是“25”?
商的小数部分总是重复出现“3”。
继续除下去,可能永远也除不完。
0
0
3
2 2 5
2 5
0
3
2 2 5
2 5
先计算,再说一说这些商的特点。
)
2 8
18
1
.
5
1 8
1 0
0
9 0
1 0
28÷18
0
5
9 0
1 0
0
5
9 0
1 0
……
……
= 1.555
……
)
7 8 . 6
11
7
.
1
7 7
1
6
1 1
5
78.6÷11
0
4
4 4
6
0
5
5 5
5
……
= 7.14545
……
0
4
4 4
6
0
5
5 5
5
……
5.333…和7.14545…都是循环小数。
一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫循环小数。
5.333…还可以写作5.3,
7.14545…还可以写作7.145。
.
.
.
想一想
两个数相除,如果不能得到整数商,所得的商会有哪些情况?
15÷16 = 。 1.5÷7 = 。
0.9375
小数部分的位数是有限的小数,叫做有限小数。
例如,0.9375是一个有限小数。
小数部分的位数是无限的小数,叫做无限小数。
例如,0.2142857142857…就是一个无限小数。
0.2142857142857…
依次不断重复出现的数字是?
3.4666 ( )
0.24382438 ( )
8.4747 ( )
0.44222 ( )
……
……
……
……
6
2438
47
2
一个循环小数的小数部分,依次不断重复出现的数字,叫做这个循环小数的循环节。例如,5.33…的循环节是3,7.14545…的循环节是45。写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位上面各记一个圆点。例如,
5.33…写作5.3,7.14545…写作7.145。
.
.
.
循环节
1÷11= 0.0909…
2÷11= 0.1818…
3÷11=______
4÷11=______
5÷11=______
用计算器计算下面各题目。
0.2727…
0.3636…
0.4545…
它们的商都是循环小数。
你发现了什么规律?
不计算,用发现的规律直接写出下面几道题的商。
6÷11=______
7÷11=______
8÷11=______
9÷11=_____
0.5454…
0.6363…
0.7272…
0.8181…
用计算器计算前4题,试着写出后2题的积。
3×7 = 。
3.3×6.7 = 。
3.33×66.7 = 。
3.333×666.7 = 。
3.3333×6666.7 = 。
3.33333×66666.7 = 。
21
22.11
222.111
2222.1111
22222.11111
222222.111111
不计算,运用规律直接填出得数。
6×7 = 42
6.6×6.7 = 44.22
6.66×66.7 = 。
6.666×666.7 = 。
444.222
4444.2222
先找规律,再按规律填数。
(1)6.25 2.5 1 0.064
(2)7 3.5 1.75 0.21875
0.4 0.16
0.875 0.4375
数字黑洞是指自然数经过某种数学运算之后陷入了一种循环的情况。例如,任意四个不同的数字,组成一个最大的数和一个最小的数,用大数减去小数。用所得结果的四位数重复上述过程,最多七步,必得6174。即:7614-1467=6174。仿佛掉进了黑洞,永远出不来。不信的话,请你试一试!
什么是“数字黑洞”?
本课小结
本课关键不在于如何使用计算器,而是要我们通过观察找出商的规律,把得出的规律应用于后续的计算。
