华东师大版八年级数学上册13.3.1等腰三角形的性质-课堂限时训练(word版含答案)
文档属性
| 名称 | 华东师大版八年级数学上册13.3.1等腰三角形的性质-课堂限时训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 72.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 23:47:27 | ||
图片预览



文档简介
13.3.1
等腰三角形的性质
知识点1:等腰三角形的性质.
知识点2:等边三角形的性质.
重
点:利用等腰三角形的性质进行相关的计算和证明.
难
点:等腰三角形中关于底和腰,底角和顶角的计算问题.
基础巩固
1.
在△ABC中,AC=BC,∠B=60°,则∠C=
.
2.
等腰三角形的一个内角是100°,则其余两个角分别是
.
3.
等腰三角形的一个底角为50°,则它的顶角的度数为
.
4.
等腰三角形的两边长分别是8cm和6cm,则其周长是
cm.
5.
等腰三角形的两边长分别是16cm和8cm,则其周长是
cm.
6.等腰三角形的对称轴是(
)
A.顶角的平分线
B.底边上的高
C.底边上的中线
D.底边上的高所在的直线
7.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是(
)
A.17cm
B.22cm
C.17cm或22cm
D.18cm
8.等腰三角形的顶角是80°,则一腰上的高与底边的夹角是(
)
A.40°
B.50°
C.60°
D.30°
9.等腰三角形的一个外角是80°,则其底角是(
)
A.100°
B.100°或40°
C.40°
D.80°
10.如图,C,E和B,D,F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,
则∠GEF的度数是(
)
10题图
A.80°
B.90°
C.100°
D.108°
11.给出下列关于等腰三角形性质的叙述:①等腰三角形的两底角相等;②等腰三角形底边上的高、底边上的中线、顶角的角平分线互相重合;③等腰三角形是轴对称图形.其中正确的有(
)
A.0个
B.1个
C.2个
D.3个
12.
已知,如图,AD∥BC,AB=AD.
求证:BD平分∠ABC.
12题图
13.已知,如图,∠CAE是△ABC的外角,AB=AC,AD∥BC.求证:∠1=∠2.
13题图
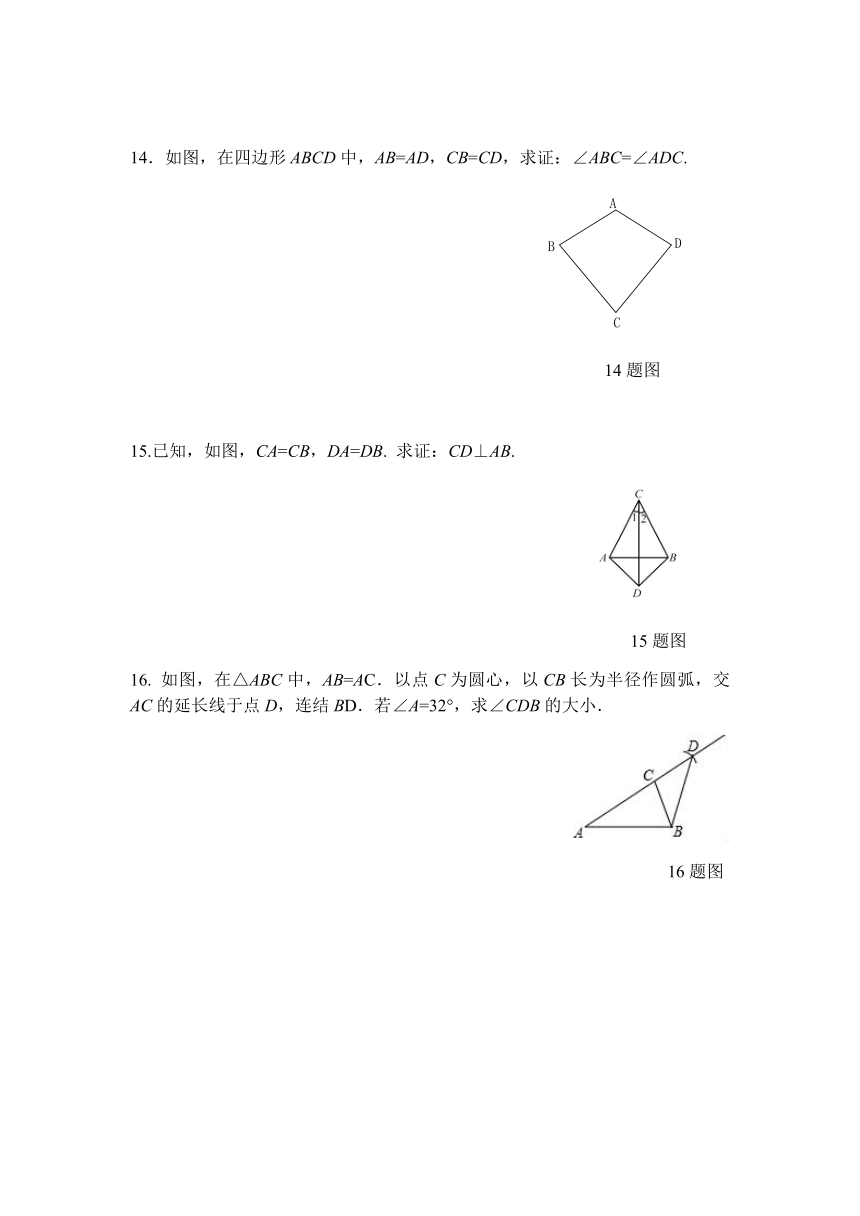
14.如图,在四边形ABCD中,AB=AD,CB=CD,求证:∠ABC=∠ADC.
14题图
15.已知,如图,CA=CB,DA=DB.
求证:CD⊥AB.
15题图
16.
如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,求∠CDB的大小.
16题图
强化提高
17.如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,
连结AD、BE,交CE和AC分别于点G、H,连结GH.
(1)请说出AD=BE的理由;
(2)试说出△BCH≌△ACG的理由.
17题图
18.如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD=AE,∠DAE=100°.当DE⊥AC时,求∠BAD和∠EDC的度数.
18题图
19.如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数.
19题图
13.3.1
等腰三角形的性质答案
1.
60°.
2.
40°,40°.
3.
80°.解析:∵等腰三角形底角相等,∴180°﹣50°×2=80°,∴顶角为80°.故填80°.
4.
22或20.
解析:当8cm为底边时,周长为8+6+6=20,当6cm为底边时,周长为6+8+8=22.
5.40.
解析:16cm的边只能做腰,不能做底边,否则不能构成三角形,周长为16+16+8=40.
6.
D.
7.
B.
8.
A.
9.
C.
10.
B.
11.
D.
12.证明:∵AB=AD(已知),∴∠ABD=∠ADB.
∵AD∥BC
(已知),
∴∠DBC=∠ADB(两直线平行,内错角相等),
∴∠ABD=∠DBC(等量代换),
∴BD平分∠ABC.
13.证明:∵AB=AC,∴∠B=∠C(等边对等角).
∵AD∥BC,∴∠B=∠1,∠C=∠2,
∴∠1=∠2.
14.证明:连接BD,∵AB=AD,
∴∠ABD=∠ADB.
∵CB=CD,∴∠CBD=∠CDB.
∴∠ABC=∠ADC.
14题图
15.证明:在△ACD和△BCD中,
∵CA=CB(已知),DA=DB(已知),CD=CD(公共边),
∴△ACD≌△BCD(S.S.S).
∴∠1=∠2(全等三角形的对应角相等),
∴CD⊥AB(三线合一).
16.
解:∵AB=AC,∠A=32°,
∴∠ABC=∠ACB=74°,
又∵BC=DC,∴∠CDB=∠CBD=∠ACB=37°.
17.解:
(1)∵△ABC和△CDE均为等边三角形,
∴AC=BC,DC=EC,∠ACB=∠ECD=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(S.A.S.),∴AD=BE.
(2)∵△ACD≌△BCE,∴∠CBH=∠CAG.
∵∠ACB=∠ECD=60°,点B、C、D在同一条直线上,
∴∠ACB=∠ECD=∠ACG=60°.
又∵BC=AC,∴△BCH≌△ACG(A.S.A).
18.解:∵△ABC是等边三角形,
∴∠B=∠BAC=∠C=60°.
又∵AD=AE,∠DAE=100°,
∴∠ADE=∠E=40°.
∵DE⊥AC,∴∠DAC=∠EAC=50°,
∴∠BAD=∠BAC-∠DAC=60°-50°=10°.
又∵∠ADC=∠B+∠BAD=70°,
∴∠EDC=∠ADC-∠ADE=30°.
19.(1)证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
在△BAE和△ACD中,
∴△BAE≌△ACD(S.A.S.).
(2)解:∵△BAE≌△ACD,
∴∠ABE=∠CAD.
∵∠BPQ为△ABP的外角,
∴∠BPQ=∠ABE+∠BAD,
∴∠BPQ=∠CAD+∠BAD=∠BAC=60°.
等腰三角形的性质
知识点1:等腰三角形的性质.
知识点2:等边三角形的性质.
重
点:利用等腰三角形的性质进行相关的计算和证明.
难
点:等腰三角形中关于底和腰,底角和顶角的计算问题.
基础巩固
1.
在△ABC中,AC=BC,∠B=60°,则∠C=
.
2.
等腰三角形的一个内角是100°,则其余两个角分别是
.
3.
等腰三角形的一个底角为50°,则它的顶角的度数为
.
4.
等腰三角形的两边长分别是8cm和6cm,则其周长是
cm.
5.
等腰三角形的两边长分别是16cm和8cm,则其周长是
cm.
6.等腰三角形的对称轴是(
)
A.顶角的平分线
B.底边上的高
C.底边上的中线
D.底边上的高所在的直线
7.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是(
)
A.17cm
B.22cm
C.17cm或22cm
D.18cm
8.等腰三角形的顶角是80°,则一腰上的高与底边的夹角是(
)
A.40°
B.50°
C.60°
D.30°
9.等腰三角形的一个外角是80°,则其底角是(
)
A.100°
B.100°或40°
C.40°
D.80°
10.如图,C,E和B,D,F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,
则∠GEF的度数是(
)
10题图
A.80°
B.90°
C.100°
D.108°
11.给出下列关于等腰三角形性质的叙述:①等腰三角形的两底角相等;②等腰三角形底边上的高、底边上的中线、顶角的角平分线互相重合;③等腰三角形是轴对称图形.其中正确的有(
)
A.0个
B.1个
C.2个
D.3个
12.
已知,如图,AD∥BC,AB=AD.
求证:BD平分∠ABC.
12题图
13.已知,如图,∠CAE是△ABC的外角,AB=AC,AD∥BC.求证:∠1=∠2.
13题图
14.如图,在四边形ABCD中,AB=AD,CB=CD,求证:∠ABC=∠ADC.
14题图
15.已知,如图,CA=CB,DA=DB.
求证:CD⊥AB.
15题图
16.
如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,求∠CDB的大小.
16题图
强化提高
17.如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,
连结AD、BE,交CE和AC分别于点G、H,连结GH.
(1)请说出AD=BE的理由;
(2)试说出△BCH≌△ACG的理由.
17题图
18.如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD=AE,∠DAE=100°.当DE⊥AC时,求∠BAD和∠EDC的度数.
18题图
19.如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数.
19题图
13.3.1
等腰三角形的性质答案
1.
60°.
2.
40°,40°.
3.
80°.解析:∵等腰三角形底角相等,∴180°﹣50°×2=80°,∴顶角为80°.故填80°.
4.
22或20.
解析:当8cm为底边时,周长为8+6+6=20,当6cm为底边时,周长为6+8+8=22.
5.40.
解析:16cm的边只能做腰,不能做底边,否则不能构成三角形,周长为16+16+8=40.
6.
D.
7.
B.
8.
A.
9.
C.
10.
B.
11.
D.
12.证明:∵AB=AD(已知),∴∠ABD=∠ADB.
∵AD∥BC
(已知),
∴∠DBC=∠ADB(两直线平行,内错角相等),
∴∠ABD=∠DBC(等量代换),
∴BD平分∠ABC.
13.证明:∵AB=AC,∴∠B=∠C(等边对等角).
∵AD∥BC,∴∠B=∠1,∠C=∠2,
∴∠1=∠2.
14.证明:连接BD,∵AB=AD,
∴∠ABD=∠ADB.
∵CB=CD,∴∠CBD=∠CDB.
∴∠ABC=∠ADC.
14题图
15.证明:在△ACD和△BCD中,
∵CA=CB(已知),DA=DB(已知),CD=CD(公共边),
∴△ACD≌△BCD(S.S.S).
∴∠1=∠2(全等三角形的对应角相等),
∴CD⊥AB(三线合一).
16.
解:∵AB=AC,∠A=32°,
∴∠ABC=∠ACB=74°,
又∵BC=DC,∴∠CDB=∠CBD=∠ACB=37°.
17.解:
(1)∵△ABC和△CDE均为等边三角形,
∴AC=BC,DC=EC,∠ACB=∠ECD=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(S.A.S.),∴AD=BE.
(2)∵△ACD≌△BCE,∴∠CBH=∠CAG.
∵∠ACB=∠ECD=60°,点B、C、D在同一条直线上,
∴∠ACB=∠ECD=∠ACG=60°.
又∵BC=AC,∴△BCH≌△ACG(A.S.A).
18.解:∵△ABC是等边三角形,
∴∠B=∠BAC=∠C=60°.
又∵AD=AE,∠DAE=100°,
∴∠ADE=∠E=40°.
∵DE⊥AC,∴∠DAC=∠EAC=50°,
∴∠BAD=∠BAC-∠DAC=60°-50°=10°.
又∵∠ADC=∠B+∠BAD=70°,
∴∠EDC=∠ADC-∠ADE=30°.
19.(1)证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
在△BAE和△ACD中,
∴△BAE≌△ACD(S.A.S.).
(2)解:∵△BAE≌△ACD,
∴∠ABE=∠CAD.
∵∠BPQ为△ABP的外角,
∴∠BPQ=∠ABE+∠BAD,
∴∠BPQ=∠CAD+∠BAD=∠BAC=60°.
