高中数学人教A版必修4第一章三角函数诱导公式练习题两套(Word版含答案)附三角函数相关公式
文档属性
| 名称 | 高中数学人教A版必修4第一章三角函数诱导公式练习题两套(Word版含答案)附三角函数相关公式 |  | |
| 格式 | doc | ||
| 文件大小 | 479.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 10:50:01 | ||
图片预览

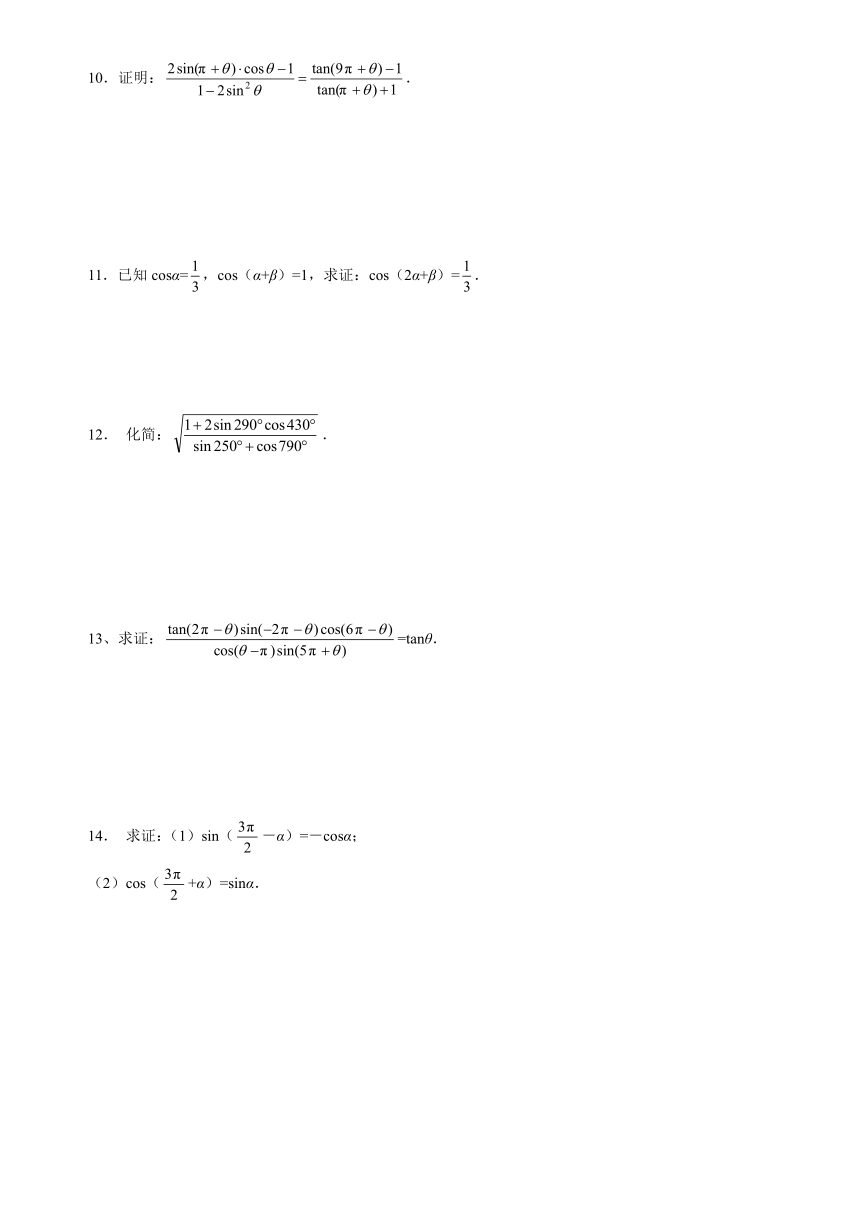


文档简介
三角函数的诱导公式1
一、选择题
1.如果|cosx|=cos(x+π),则x的取值集合是( )
A.-+2kπ≤x≤+2kπ B.-+2kπ≤x≤+2kπ
C. +2kπ≤x≤+2kπ D.(2k+1)π≤x≤2(k+1)π(以上k∈Z)
2.sin(-)的值是( )
A. B.- C. D.-
3.下列三角函数:
①sin(nπ+);②cos(2nπ+);③sin(2nπ+);④cos[(2n+1)π-];
⑤sin[(2n+1)π-](n∈Z).
其中函数值与sin的值相同的是( )
A.①② B.①③④ C.②③⑤ D.①③⑤
4.若cos(π+α)=-,且α∈(-,0),则tan(+α)的值为( )
A.- B. C.- D.
5.设A、B、C是三角形的三个内角,下列关系恒成立的是( )
A.cos(A+B)=cosC B.sin(A+B)=sinC C.tan(A+B)=tanC D.sin=sin
6.函数f(x)=cos(x∈Z)的值域为( )
A.{-1,-,0,,1} B.{-1,-,,1}
C.{-1,-,0,,1} D.{-1,-,,1}
二、填空题
7.若α是第三象限角,则=_________.
8.sin21°+sin22°+sin23°+…+sin289°=_________.
三、解答题
9.求值:sin(-660°)cos420°-tan330°cot(-690°).
10.证明:.
11.已知cosα=,cos(α+β)=1,求证:cos(2α+β)=.
12. 化简:.
13、求证:=tanθ.
14. 求证:(1)sin(-α)=-cosα;
(2)cos(+α)=sinα.
参考答案1
一、选择题
1.C 2.A 3.C 4.B 5.B 6.B
二、填空题
7.-sinα-cosα 8.
三、解答题
9.+1.
10.证明:左边=
=-,
右边=,
左边=右边,∴原等式成立.
11.证明:∵cos(α+β)=1,∴α+β=2kπ.
∴cos(2α+β)=cos(α+α+β)=cos(α+2kπ)=cosα=.
12.解:
=
=
=
==-1.
13.证明:左边==tanθ=右边,
∴原等式成立.
14证明:(1)sin(-α)=sin[π+(-α)]=-sin(-α)=-cosα.
(2)cos(+α)=cos[π+(+α)]=-cos(+α)=sinα.
三角函数的诱导公式2
一、选择题:
1.已知sin(+α)=,则sin(-α)值为( )
A. B. — C. D. —
2.cos(+α)= —,<α<,sin(-α) 值为( )
A. B. C. D. —
3.化简:得( )
A.sin2+cos2 B.cos2-sin2 C.sin2-cos2 D.± (cos2-sin2)
4.已知α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sinα=sinβ B. sin(α-) =sinβ C.cosα=cosβ D. cos(-α) =-cosβ
5.设tanθ=-2, <θ<0,那么sinθ+cos(θ-)的值等于( ),
A. (4+) B. (4-) C. (4±) D. (-4)
二、填空题:
6.cos(-x)= ,x∈(-,),则x的值为 .
7.tanα=m,则 .
8.|sinα|=sin(-+α),则α的取值范围是 .
三、解答题:
9..
10.已知:sin(x+)=,求sin(+cos2(-x)的值.
11. 求下列三角函数值:
(1)sin;(2)cos;(3)tan(-);
12. 求下列三角函数值:
(1)sin·cos·tan;
(2)sin[(2n+1)π-].
13.设f(θ)=,求f()的值.
参考答案2
1.C 2.A 3.C 4.C 5.A
6.± 7. 8.[(2k-1) ,2k]
9.原式=== sinα 10.
11.解:(1)sin=sin(2π+)=sin=.
(2)cos=cos(4π+)=cos=.
(3)tan(-)=cos(-4π+)=cos=.
(4)sin(-765°)=sin[360°×(-2)-45°]=sin(-45°)=-sin45°=-.
注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.
12.解:(1)sin·cos·tan=sin(π+)·cos(4π+)·tan(π+)
=(-sin)·cos·tan=(-)··1=-.
(2)sin[(2n+1)π-]=sin(π-)=sin=.
13.解:f(θ)=
=
=
=
=
=
=cosθ-1,
∴f()=cos-1=-1=-.
三角函数公式
同角三角函数基本关系式
sin2α+cos2α=1
=tanα
tanαcotα=1
诱导公式 (奇变偶不变,符号看象限)
sin(π-α)=sinα sin(π+α)=-sinα
cos(π-α)=-cosα cos(π+α)=-cosα
tan(π-α)=-tanα tan(π+α)=tanα
sin(2π-α)=-sinα sin(2π+α)=sinα
cos(2π-α)=cosα cos(2π+α)=cosα
tan(2π-α)=-tanα tan(2π+α)=tanα
(二) sin(-α)=cosα sin(+α)=cosα
cos(-α)=sinα cos(+α)=- sinα
tan(-α)=cotα tan(+α)=-cotα
sin(-α)=-cosα sin(+α)=-cosα
cos(-α)=-sinα cos(+α)=sinα
tan(-α)=cotα tan(+α)=-cotα
sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα
两角和与差的三角函数
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
sin (α+β)=sinαcosβ+cosαsinβ
sin (α-β)=sinαcosβ-cosαsinβ
tan(α+β)=
tan(α-β)=
二倍角公式
sin2α=2sinαcosα
cos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2α
tan2α=
公式的变形
升幂公式:1+cos2α=2cos2α 1—cos2α=2sin2α
降幂公式:cos2α= sin2α=
正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ)
tanα-tanβ=tan(α-β)(1+tanαtanβ)
万能公式(用tanα表示其他三角函数值)
sin2α= cos2α= tan2α=
插入辅助角公式
asinx+bcosx=sin(x+φ) (tanφ= )
特殊地:sinx±cosx=sin(x±)
熟悉形式的变形(如何变形)
1±sinx±cosx 1±sinx 1±cosx tanx+cotx
若A、B是锐角,A+B=,则(1+tanA)(1+tanB)=2
在三角形中的结论
若:A+B+C=π , =则有
tanA+tanB+tanC=tanAtanBtanC
tantan+tantan+tantan=1
一、选择题
1.如果|cosx|=cos(x+π),则x的取值集合是( )
A.-+2kπ≤x≤+2kπ B.-+2kπ≤x≤+2kπ
C. +2kπ≤x≤+2kπ D.(2k+1)π≤x≤2(k+1)π(以上k∈Z)
2.sin(-)的值是( )
A. B.- C. D.-
3.下列三角函数:
①sin(nπ+);②cos(2nπ+);③sin(2nπ+);④cos[(2n+1)π-];
⑤sin[(2n+1)π-](n∈Z).
其中函数值与sin的值相同的是( )
A.①② B.①③④ C.②③⑤ D.①③⑤
4.若cos(π+α)=-,且α∈(-,0),则tan(+α)的值为( )
A.- B. C.- D.
5.设A、B、C是三角形的三个内角,下列关系恒成立的是( )
A.cos(A+B)=cosC B.sin(A+B)=sinC C.tan(A+B)=tanC D.sin=sin
6.函数f(x)=cos(x∈Z)的值域为( )
A.{-1,-,0,,1} B.{-1,-,,1}
C.{-1,-,0,,1} D.{-1,-,,1}
二、填空题
7.若α是第三象限角,则=_________.
8.sin21°+sin22°+sin23°+…+sin289°=_________.
三、解答题
9.求值:sin(-660°)cos420°-tan330°cot(-690°).
10.证明:.
11.已知cosα=,cos(α+β)=1,求证:cos(2α+β)=.
12. 化简:.
13、求证:=tanθ.
14. 求证:(1)sin(-α)=-cosα;
(2)cos(+α)=sinα.
参考答案1
一、选择题
1.C 2.A 3.C 4.B 5.B 6.B
二、填空题
7.-sinα-cosα 8.
三、解答题
9.+1.
10.证明:左边=
=-,
右边=,
左边=右边,∴原等式成立.
11.证明:∵cos(α+β)=1,∴α+β=2kπ.
∴cos(2α+β)=cos(α+α+β)=cos(α+2kπ)=cosα=.
12.解:
=
=
=
==-1.
13.证明:左边==tanθ=右边,
∴原等式成立.
14证明:(1)sin(-α)=sin[π+(-α)]=-sin(-α)=-cosα.
(2)cos(+α)=cos[π+(+α)]=-cos(+α)=sinα.
三角函数的诱导公式2
一、选择题:
1.已知sin(+α)=,则sin(-α)值为( )
A. B. — C. D. —
2.cos(+α)= —,<α<,sin(-α) 值为( )
A. B. C. D. —
3.化简:得( )
A.sin2+cos2 B.cos2-sin2 C.sin2-cos2 D.± (cos2-sin2)
4.已知α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sinα=sinβ B. sin(α-) =sinβ C.cosα=cosβ D. cos(-α) =-cosβ
5.设tanθ=-2, <θ<0,那么sinθ+cos(θ-)的值等于( ),
A. (4+) B. (4-) C. (4±) D. (-4)
二、填空题:
6.cos(-x)= ,x∈(-,),则x的值为 .
7.tanα=m,则 .
8.|sinα|=sin(-+α),则α的取值范围是 .
三、解答题:
9..
10.已知:sin(x+)=,求sin(+cos2(-x)的值.
11. 求下列三角函数值:
(1)sin;(2)cos;(3)tan(-);
12. 求下列三角函数值:
(1)sin·cos·tan;
(2)sin[(2n+1)π-].
13.设f(θ)=,求f()的值.
参考答案2
1.C 2.A 3.C 4.C 5.A
6.± 7. 8.[(2k-1) ,2k]
9.原式=== sinα 10.
11.解:(1)sin=sin(2π+)=sin=.
(2)cos=cos(4π+)=cos=.
(3)tan(-)=cos(-4π+)=cos=.
(4)sin(-765°)=sin[360°×(-2)-45°]=sin(-45°)=-sin45°=-.
注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.
12.解:(1)sin·cos·tan=sin(π+)·cos(4π+)·tan(π+)
=(-sin)·cos·tan=(-)··1=-.
(2)sin[(2n+1)π-]=sin(π-)=sin=.
13.解:f(θ)=
=
=
=
=
=
=cosθ-1,
∴f()=cos-1=-1=-.
三角函数公式
同角三角函数基本关系式
sin2α+cos2α=1
=tanα
tanαcotα=1
诱导公式 (奇变偶不变,符号看象限)
sin(π-α)=sinα sin(π+α)=-sinα
cos(π-α)=-cosα cos(π+α)=-cosα
tan(π-α)=-tanα tan(π+α)=tanα
sin(2π-α)=-sinα sin(2π+α)=sinα
cos(2π-α)=cosα cos(2π+α)=cosα
tan(2π-α)=-tanα tan(2π+α)=tanα
(二) sin(-α)=cosα sin(+α)=cosα
cos(-α)=sinα cos(+α)=- sinα
tan(-α)=cotα tan(+α)=-cotα
sin(-α)=-cosα sin(+α)=-cosα
cos(-α)=-sinα cos(+α)=sinα
tan(-α)=cotα tan(+α)=-cotα
sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα
两角和与差的三角函数
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
sin (α+β)=sinαcosβ+cosαsinβ
sin (α-β)=sinαcosβ-cosαsinβ
tan(α+β)=
tan(α-β)=
二倍角公式
sin2α=2sinαcosα
cos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2α
tan2α=
公式的变形
升幂公式:1+cos2α=2cos2α 1—cos2α=2sin2α
降幂公式:cos2α= sin2α=
正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ)
tanα-tanβ=tan(α-β)(1+tanαtanβ)
万能公式(用tanα表示其他三角函数值)
sin2α= cos2α= tan2α=
插入辅助角公式
asinx+bcosx=sin(x+φ) (tanφ= )
特殊地:sinx±cosx=sin(x±)
熟悉形式的变形(如何变形)
1±sinx±cosx 1±sinx 1±cosx tanx+cotx
若A、B是锐角,A+B=,则(1+tanA)(1+tanB)=2
在三角形中的结论
若:A+B+C=π , =则有
tanA+tanB+tanC=tanAtanBtanC
tantan+tantan+tantan=1
