人教A版高中数学必修2第二章《点、直线、平面之间的位置关系》测试题(Word版含答案)
文档属性
| 名称 | 人教A版高中数学必修2第二章《点、直线、平面之间的位置关系》测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 793.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览




文档简介
第二章《点、直线、平面之间的位置关系》测试题
一、单选题
1.下列结论中正确的是
A.若直线上有无数个点不在平面内,则//.
B.若直线与平面平行,则直线与平面内的任意一条直线都平行.
C.若直线与平面垂直,则直线与平面内的任意一条直线都垂直.
D.四边形确定一个平面.
2.如图所示,将无盖正方体纸盒展开,直线AB、CD在原正方体中的位置关系是( )
A.平行
B.相交且垂直
C.异面直线
D.相交成60°角
3.已知在底面为菱形的直四棱柱中,
,若,则异面直线与所成的角为(
)
A.
B.
C.
D.
4.矩形中,,,沿将矩形折起,使面面,则四面体的外接球的体积为(
)
A.
B.
C.
D.
5.如图,正三棱柱各条棱的长度均相等,为的中点,分别是线段和线段的动点(含端点),且满足,当运动时,下列结论中不正确的是
A.在内总存在与平面平行的线段
B.平面平面
C.三棱锥的体积为定值
D.可能为直角三角形
6.如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E、F分别是SC和AB的中点,则EF的长是(
)
A.
B.
C.
D.
7.三棱锥中,则在底面的投影一定在三角形的(
)
A.内心
B.外心
C.垂心
D.重心
8.如图,在棱长为2的正方体中,的中点是,过点作与截面平行的截面,则该截面的面积为(
)
A.
B.
C.
D.
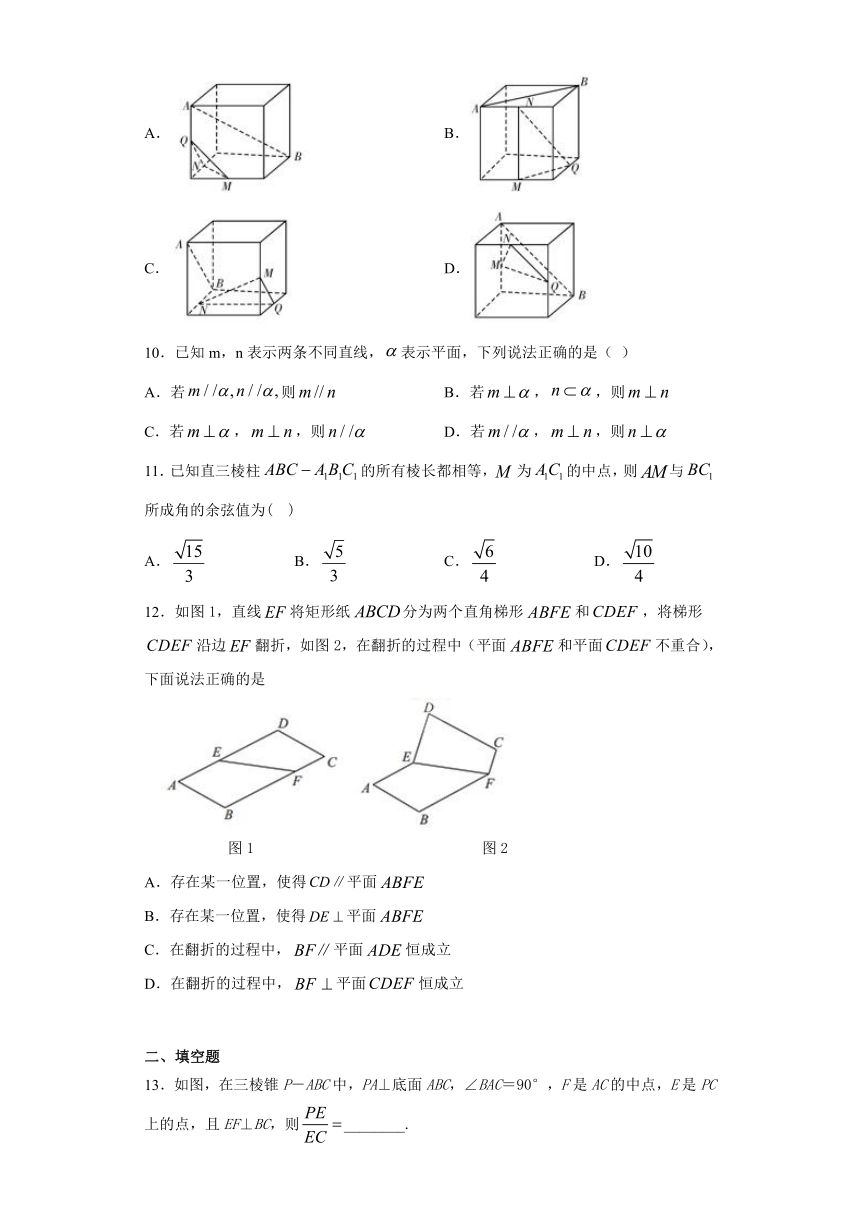
9.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是(
)
A.
B.
C.
D.
10.已知m,n表示两条不同直线,表示平面,下列说法正确的是(
)
A.若则
B.若,,则
C.若,,则
D.若,,则
11.已知直三棱柱的所有棱长都相等,为的中点,则与所成角的余弦值为(
)
A.
B.
C.
D.
12.如图1,直线将矩形纸分为两个直角梯形和,将梯形沿边翻折,如图2,在翻折的过程中(平面和平面不重合),下面说法正确的是
图1
图2
A.存在某一位置,使得平面
B.存在某一位置,使得平面
C.在翻折的过程中,平面恒成立
D.在翻折的过程中,平面恒成立
二、填空题
13.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°,F是AC的中点,E是PC上的点,且EF⊥BC,则________.
14.已知四棱锥的底面边长都为2,,,且,是的中点,则异面直线与所成的角为_______.
15.如图,DC⊥平面ABC,EB∥DC,EB=2DC,P,Q分别为AE,AB的中点.则直线DP与平面ABC的位置关系是________.
16.在直三棱柱中,底面为等腰直角三角形,
,
,
若、、别是棱、、的中点,则下列四个命题:
;
②三棱锥的外接球的表面积为;
③三棱锥的体积为;
④直线与平面所成角为
其中正确的命题有__________.(把所有正确命题的序号填在答题卡上)
三、解答题
17.如图所示,在正方体中,为的中点,为的中点.
求证:(1)四点共面;
(2)三线共点.
18.如图,在四棱锥P-ABCD中,AD∥BC,ADC=PAB=90°,BC=CD=AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
19.如图,在三棱柱中,、分别是棱,的中点,求证:
(1)平面;
(2)平面平面.
20.如图,四边形为矩形,且平面,
,为的中点.
(1)求证:;
(2)求三棱锥的体积;
(3)探究在上是否存在点,使得平面,并说明理由.
21.如图,在四棱锥中,四边形为正方形,平面,,是上一点.
(1)若,求证:平面;
(2)若为的中点,且,求三棱锥的体积.
22.如图,在四棱锥中,底面为矩形,平面平面,,,、分别为、的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面平面;
(Ⅲ)求证:平面.
参考答案
1.C
2.D
3.D
4.A
5.D
6.B
7.C
8.C
9.A
10.B11.D
12.C
13.1
14.
15.平行
16.①②③
17.
证明:(1)连接.
∵分别是和的中点,
∴.
又,
∴四边形是平行四边形,
∴,
∴,
∴与确定一个平面,
∴四点共面.
(2)由(1)知,,且,
∴直线与必相交,设.
∵平面,,
∴平面.
又平面,,
∴平面,即是平面与平面的公共点,
又平面平面,
∴,
∴三线共点.
18.解:(Ⅰ)在梯形ABCD中,AB与CD不平行.
延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.
理由如下:
由已知,BC∥ED,且BC=ED.
所以四边形BCDE是平行四边形.
从而CM∥EB.
又EB平面PBE,CM
平面PBE,
所以CM∥平面PBE.
(说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点)
(Ⅱ)方法一:
由已知,CD⊥PA,CD⊥AD,PAAD=A,
所以CD⊥平面PAD.
从而CD⊥PD.
所以PDA是二面角P-CD-A的平面角.
所以PDA=45°.
设BC=1,则在Rt△PAD中,PA=AD=2.
过点A作AH⊥CE,交CE的延长线于点H,连接PH.
易知PA⊥平面ABCD,
从而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
过A作AQ⊥PH于Q,则AQ⊥平面PCE.
所以APH是PA与平面PCE所成的角.
在Rt△AEH中,AEH=45°,AE=1,
所以AH=.
在Rt△PAH中,PH==
,
所以sinAPH=
=.
19.
证明:(1)设与的交点为,连结,
∵四边形为平行四边形,∴为中点,
又是的中点,∴是三角形的中位线,则,
又∵平面,平面,
∴平面;
(2)∵为线段的中点,点是的中点,
∴且,则四边形为平行四边形,
∴,
又∵平面,平面,
∴平面.
又平面,,且平面,平面,
∴平面平面.
20.
(1)连结,∵为的中点,,
∴为等腰直角三角形,
则,同理可得,∴,∴,
又,且,
∴,
又∵,∴,又,∴.
(2)由(1)知为腰长为1的等腰直角三角形,
∴,而是三棱锥的高,
∴.
(3)在上存在中点,使得.理由如下:
取的中点,连结.
∵是的中点,
∴,且,
又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=AD,
所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH,
又EG平面PCD,CH平面PCD,所以EG//平面PCD.
21.
(1)证明:连接,由平面,平面得,
又,,
∴平面,得,
又,,
∴平面.
(2)解:由为的中点得
.
22.
(Ⅰ)∵,且为的中点,∴.
∵底面为矩形,∴,∴;
(Ⅱ)∵底面为矩形,∴.
∵平面平面,平面平面,平面,
∴平面,又平面,∴.
又,,、平面,平面,
∵平面,∴平面平面;
(Ⅲ)如图,取中点,连接.
∵分别为和的中点,∴,且.
∵四边形为矩形,且为的中点,∴,
∴,且,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
一、单选题
1.下列结论中正确的是
A.若直线上有无数个点不在平面内,则//.
B.若直线与平面平行,则直线与平面内的任意一条直线都平行.
C.若直线与平面垂直,则直线与平面内的任意一条直线都垂直.
D.四边形确定一个平面.
2.如图所示,将无盖正方体纸盒展开,直线AB、CD在原正方体中的位置关系是( )
A.平行
B.相交且垂直
C.异面直线
D.相交成60°角
3.已知在底面为菱形的直四棱柱中,
,若,则异面直线与所成的角为(
)
A.
B.
C.
D.
4.矩形中,,,沿将矩形折起,使面面,则四面体的外接球的体积为(
)
A.
B.
C.
D.
5.如图,正三棱柱各条棱的长度均相等,为的中点,分别是线段和线段的动点(含端点),且满足,当运动时,下列结论中不正确的是
A.在内总存在与平面平行的线段
B.平面平面
C.三棱锥的体积为定值
D.可能为直角三角形
6.如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E、F分别是SC和AB的中点,则EF的长是(
)
A.
B.
C.
D.
7.三棱锥中,则在底面的投影一定在三角形的(
)
A.内心
B.外心
C.垂心
D.重心
8.如图,在棱长为2的正方体中,的中点是,过点作与截面平行的截面,则该截面的面积为(
)
A.
B.
C.
D.
9.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是(
)
A.
B.
C.
D.
10.已知m,n表示两条不同直线,表示平面,下列说法正确的是(
)
A.若则
B.若,,则
C.若,,则
D.若,,则
11.已知直三棱柱的所有棱长都相等,为的中点,则与所成角的余弦值为(
)
A.
B.
C.
D.
12.如图1,直线将矩形纸分为两个直角梯形和,将梯形沿边翻折,如图2,在翻折的过程中(平面和平面不重合),下面说法正确的是
图1
图2
A.存在某一位置,使得平面
B.存在某一位置,使得平面
C.在翻折的过程中,平面恒成立
D.在翻折的过程中,平面恒成立
二、填空题
13.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°,F是AC的中点,E是PC上的点,且EF⊥BC,则________.
14.已知四棱锥的底面边长都为2,,,且,是的中点,则异面直线与所成的角为_______.
15.如图,DC⊥平面ABC,EB∥DC,EB=2DC,P,Q分别为AE,AB的中点.则直线DP与平面ABC的位置关系是________.
16.在直三棱柱中,底面为等腰直角三角形,
,
,
若、、别是棱、、的中点,则下列四个命题:
;
②三棱锥的外接球的表面积为;
③三棱锥的体积为;
④直线与平面所成角为
其中正确的命题有__________.(把所有正确命题的序号填在答题卡上)
三、解答题
17.如图所示,在正方体中,为的中点,为的中点.
求证:(1)四点共面;
(2)三线共点.
18.如图,在四棱锥P-ABCD中,AD∥BC,ADC=PAB=90°,BC=CD=AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
19.如图,在三棱柱中,、分别是棱,的中点,求证:
(1)平面;
(2)平面平面.
20.如图,四边形为矩形,且平面,
,为的中点.
(1)求证:;
(2)求三棱锥的体积;
(3)探究在上是否存在点,使得平面,并说明理由.
21.如图,在四棱锥中,四边形为正方形,平面,,是上一点.
(1)若,求证:平面;
(2)若为的中点,且,求三棱锥的体积.
22.如图,在四棱锥中,底面为矩形,平面平面,,,、分别为、的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面平面;
(Ⅲ)求证:平面.
参考答案
1.C
2.D
3.D
4.A
5.D
6.B
7.C
8.C
9.A
10.B11.D
12.C
13.1
14.
15.平行
16.①②③
17.
证明:(1)连接.
∵分别是和的中点,
∴.
又,
∴四边形是平行四边形,
∴,
∴,
∴与确定一个平面,
∴四点共面.
(2)由(1)知,,且,
∴直线与必相交,设.
∵平面,,
∴平面.
又平面,,
∴平面,即是平面与平面的公共点,
又平面平面,
∴,
∴三线共点.
18.解:(Ⅰ)在梯形ABCD中,AB与CD不平行.
延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.
理由如下:
由已知,BC∥ED,且BC=ED.
所以四边形BCDE是平行四边形.
从而CM∥EB.
又EB平面PBE,CM
平面PBE,
所以CM∥平面PBE.
(说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点)
(Ⅱ)方法一:
由已知,CD⊥PA,CD⊥AD,PAAD=A,
所以CD⊥平面PAD.
从而CD⊥PD.
所以PDA是二面角P-CD-A的平面角.
所以PDA=45°.
设BC=1,则在Rt△PAD中,PA=AD=2.
过点A作AH⊥CE,交CE的延长线于点H,连接PH.
易知PA⊥平面ABCD,
从而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
过A作AQ⊥PH于Q,则AQ⊥平面PCE.
所以APH是PA与平面PCE所成的角.
在Rt△AEH中,AEH=45°,AE=1,
所以AH=.
在Rt△PAH中,PH==
,
所以sinAPH=
=.
19.
证明:(1)设与的交点为,连结,
∵四边形为平行四边形,∴为中点,
又是的中点,∴是三角形的中位线,则,
又∵平面,平面,
∴平面;
(2)∵为线段的中点,点是的中点,
∴且,则四边形为平行四边形,
∴,
又∵平面,平面,
∴平面.
又平面,,且平面,平面,
∴平面平面.
20.
(1)连结,∵为的中点,,
∴为等腰直角三角形,
则,同理可得,∴,∴,
又,且,
∴,
又∵,∴,又,∴.
(2)由(1)知为腰长为1的等腰直角三角形,
∴,而是三棱锥的高,
∴.
(3)在上存在中点,使得.理由如下:
取的中点,连结.
∵是的中点,
∴,且,
又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=AD,
所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH,
又EG平面PCD,CH平面PCD,所以EG//平面PCD.
21.
(1)证明:连接,由平面,平面得,
又,,
∴平面,得,
又,,
∴平面.
(2)解:由为的中点得
.
22.
(Ⅰ)∵,且为的中点,∴.
∵底面为矩形,∴,∴;
(Ⅱ)∵底面为矩形,∴.
∵平面平面,平面平面,平面,
∴平面,又平面,∴.
又,,、平面,平面,
∵平面,∴平面平面;
(Ⅲ)如图,取中点,连接.
∵分别为和的中点,∴,且.
∵四边形为矩形,且为的中点,∴,
∴,且,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
